More details of the ZORA relativistic Hamiltonian

Relativistic effects can be treated efficiently with the ZORA Hamiltonian in ADF and BAND.

The ZORA equation is the zeroth order regular approximation to the Dirac equation. The relativistic and non-relativistic Kohn-Sham DFT equations can be written as:

[ T + V^KS] φ_i = ε_i φ_i

The potential V^KS is the local Kohn-Sham potential, T is the kinetic energy operator, which is different for each relativistic method:

T^Dirac = σ⋅p c²/(2c² + ε_i – V^KS) σ⋅p
T^ZORA = σ⋅p c²/(2c² – V^KS) σ⋅p
T^NR = p²/2

T^Dirac is the energy dependent Dirac kinetic energy operator, T^ZORA is the ZORA kinetic energy operator, and T^NR is the non-relativistic kinetic energy operator.

The scaled ZORA spinor energy ε_i^scaled is:

ε_i^scaled = ε_i^ZORA / < φ_i | σ⋅p c²/(2c² – V^KS)² σ⋅p | φ_i >

The scaled ZORA spinor energies are exactly equal to the Dirac energies for hydrogen like systems,
where V^KS = -Z/r.

A magnetic field can be included by minimal substitution for a negatively charged particle:

p → Π = p + A/c

The ZORA kinetic energy can be split in a scalar relativistic part T^SR and a spin-orbit coupling T^SO term:

T^ZORA = T^SR + T^SO = p⋅ c²/(2c² – V^KS) p + c²/(2c² – V^KS)² σ⋅ (∇ V^KS × p )

Spin-orbit coupling

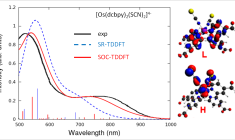
Spin-orbit coupling results from the interaction of the electron magnetic moments with the magnetic field generated by their own orbital motion. The computation is more involved than for scalar relativistic or non-relativistic calculations because spin-orbit coupling does not have the ordinary molecular symmetry. Instead, it is invariant under the molecular point double group, which affects both spin and spatial coordinates. One of its effects is to split energies of the molecule that would otherwise be identical in energy. This interaction is responsible for many of the details of spectroscopic properties.

• ADF uses double group symmetry and provides symmetry labels
• spin-orbit coupling is part of the ZORA Hamiltonian
• spin-orbit coupling can be included for most spectroscopic properties
• all electron relativistic basis sets for all elements
• spin-orbit coupling matrix elements with perturbative spin-orbit coupling TDDFT
• singlet-triplet contributions for spin-orbit coupled excitations

Other relativistic Hamiltonians

In ADF one can also use the Pauli and X2C relativistic approximations.

References

For further technical details see the original publications by SCM developer Erik van Lenthe.

E. van Lenthe, E.J. Baerends and J.G. Snijders, Relativistic regular two-component Hamiltonians, Journal of Chemical Physics 99, 4597 (1993)

E. van Lenthe, E.J. Baerends and J.G. Snijders, Relativistic total energy using regular approximations, Journal of Chemical Physics 101, 9783 (1994)

E. van Lenthe, E.J. Baerends, and J.G. Snijders, Construction of the Foldy-Wouthuysen transformation and solution of the Dirac equation using large components only, Journal of Chemical Physics 105, 2373 (1996)

E. van Lenthe, R. van Leeuwen, E.J. Baerends and J.G. Snijders, Relativistic regular two-component Hamiltonians, International Journal of Quantum Chemistry 57, 281 (1996)

E. van Lenthe, A.E. Ehlers and E.J. Baerends, Geometry optimization in the Zero Order Regular Approximation for relativistic effects, Journal of Chemical Physics 110, 8943 (1999)

L. Visscher and E. van Lenthe, On the distinction between scalar and spin-orbit relativistic effects, Chemical Physics Letters 306, 357 (1999)