3D field visualization with BAND¶
With ADFView you can visualize three-dimensional fields from the results of a BAND Calculation (runkf file).
Following is a list of relevant fields, with a short explanation and illustrative pictures (from a simple non-periodic H2 calculation). All fields are in atomic units (a.u.).
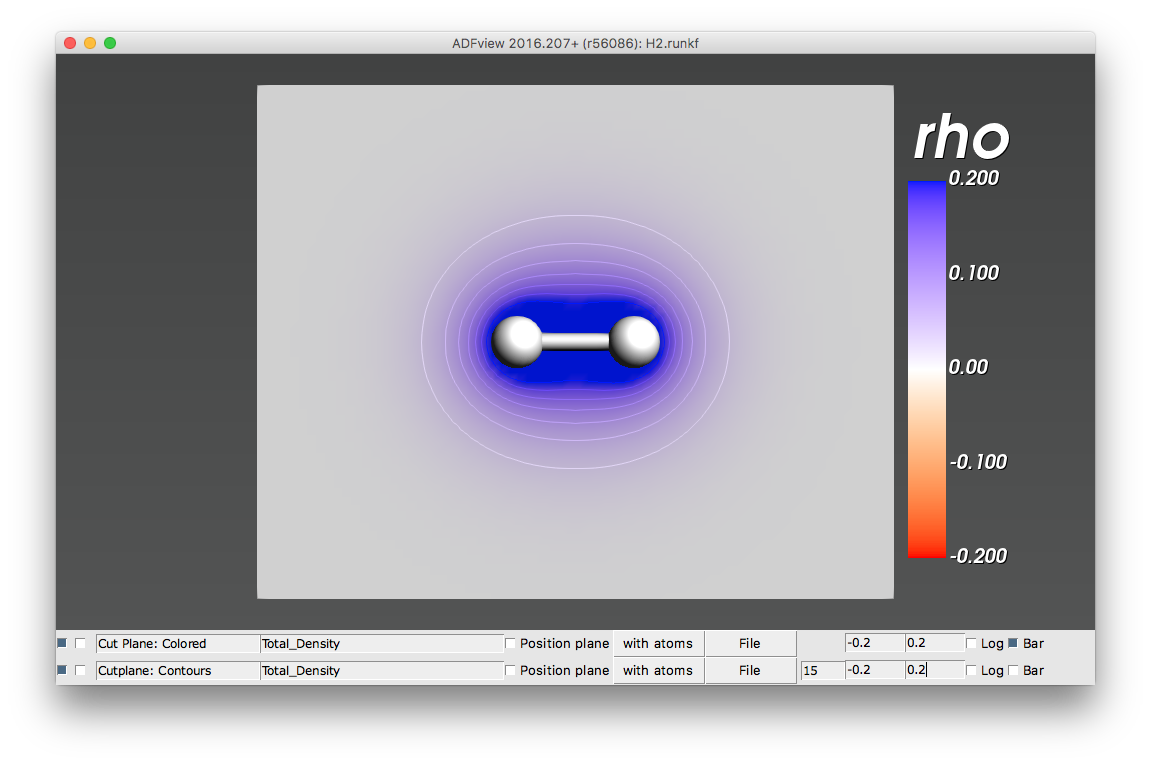
- Total_Density (rho)
The electronic density \(\rho (r)\). The integral of the electronic density over the whole space (or, for periodic systems, over the unit cell) equals the total number of electrons (valence + core).
- Deformation density (rho(deformation))
The deformation density is the difference between total density \(\rho (r)\) and reference density \(\rho_\text{reference} (r)\)
\[\rho_\text{deformation} (r) = \rho (r) - \rho_\text{reference} (r)\]The reference density \(\rho_\text{reference} (r)\) is defined as the sum of densities of spherical spin-unrestricted isolated atoms.
The deformation density is electrically neutral, i.e. its integral over the whole space (or, for periodic systems, over the unit cell) is zero. Positive values of deformation density indicate density accumulation wrt isolated atoms; negative values represent density depletion. In our H2 example, the deformation density shows how there is electron accumulation in the bonding region between the two hydrogen atoms.

- SCF_CoulombPot (v(coulomb))
The total Coulomb potential (nuclear + electronic potentials). BANDs convention for the Coulomb potential: the potential of positive charges (like nuclei) is negative, while the potential of negative charges (like electrons) is positive. In our example, the nuclear potential (negative) is larger than the electronic potential (positive) in the region of space near the H2 molecule.

Note
The sign convention for potentials in BAND is the opposite to the ADF sign convention.
- SCF_CoulombDeformation (v(coulomb/deformation))
The Coulomb potential originating from the (overall neutral) deformation density.

- xc pot (vxc(rho))
The Exchange Correlation (XC) potential. Electrons are attracted by negative XC potentials (just like they are attracted by the negative nuclear Coulomb potential)

- Orbitals (occupied/virtual)
The Kohn-Sham orbitals.
Note
Be aware that there is an over-all arbitrariness in the sign of the orbitals
Here we show the occupied and first virtual orbital of H2.

