Example: DOS and transmission: Aluminium¶
As an example of a non-self-consistent Green’s function calculation, we will look at the density of states (DOS) and transmission of an infinite 1D chain of Aluminum atoms.
First we need to perform a single-point calculation with ADF on a principal layer, consisting, in this case, of four atoms. Since bulk Aluminum has an FCC structure with a lattice constant of 4.05 Angstrom, the nearest neighbor distance is approximately 2.83 Angstrom. green requires SYMMETRY NOSYM, so we have the following input file for the principal layer:
$ADFBIN/adf << eor
TITLE Principal layer
ATOMS
Al -4.290000 0.000000 0.000000
Al -1.430000 0.000000 0.000000
Al 1.430000 0.000000 0.000000
Al 4.290000 0.000000 0.000000
END
SYMMETRY NOSYM
BASIS
Type DZP
Core Large
CreateOutput None
END
eor
mv TAPE21 layer.t21
The bulk contact geometry consists of three principal layers:
$ADFBIN/adf << eor
TITLE Bulk
ATOMS
Al -15.730000 0.000000 0.000000 f=left
Al -12.870000 0.000000 0.000000 f=left
Al -10.010000 0.000000 0.000000 f=left
Al -7.150000 0.000000 0.000000 f=left
Al -4.290000 0.000000 0.000000 f=center
Al -1.430000 0.000000 0.000000 f=center
Al 1.430000 0.000000 0.000000 f=center
Al 4.290000 0.000000 0.000000 f=center
Al 7.150000 0.000000 0.000000 f=right
Al 10.010000 0.000000 0.000000 f=right
Al 12.870000 0.000000 0.000000 f=right
Al 15.730000 0.000000 0.000000 f=right
END
SYMMETRY NOSYM
FRAGMENTS
left layer.t21
center layer.t21
right layer.t21
END
SCF
Iterations 100
END
eor
mv TAPE21 bulk.t21
Notice that we have increased the number of SCF iterations. The combination of SYMMETRY NOSYM with a 1D chain of metal atoms generally leads to convergence problems. This is the main reason why the principal layer consists of only four atoms. Fortunately, for larger 3D contacts, the convergence is generally better.
From the bulk TAPE21 file green can calculate the self-energies of the left and right contacts. As discussed in the introduction, the self-energy of the left contact needs the center and right fragments of the bulk calculation, and the self-energy of the right contact needs the center and left fragments. Since we need a self-energy matrix for every energy for which we want to calculate the DOS and transmission, already here we have to specify the energy range. We take 1000 points between -0.4 and 0 Hartree.
$ADFBIN/green << eor
SURFACE bulk.t21
FRAGMENTS center right
END
EPS -0.4 0 1000
ETA 1e-6
eor
mv SURFACE left.kf
$ADFBIN/green << eor
SURFACE bulk.t21
FRAGMENTS center left
END
EPS -0.4 0 1000
ETA 1e-6
eor
mv SURFACE right.kf
Since we want to calculate the DOS and transmission of bare aluminum, we can reuse the bulk.t21 file for the extended molecule. We couple the left self-energy to the “left” fragment and the right self-energy to the “right” fragment in bulk.t21. Since we performed restricted ADF calculations, there is no difference between spin-A and spin-B and we can omit spin-B from the calculation.
$ADFBIN/green << eor
DOS bulk.t21
TRANS bulk.t21
EPS -0.4 0 1000
ETA 1e-6
LEFT left.kf
FRAGMENT left
END
RIGHT right.kf
FRAGMENT right
END
NOSAVE DOS_B, TRANS_B
eor
The resulting DOS and transmission are shown in the following figure:
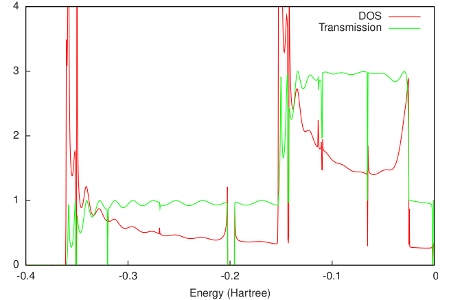
As would be expected for a 1D system, the DOS shows Van Hove singularities at the band edges. Apart from oscillations due to the finite size of the system in ADF, the transmission only reaches integer values. Between approximately -0.35 and -0.15 Hartree, only the sigma channel contributes to the transmission. Above -0.15 Hartree also the two pi channels start to contribute.