Charge transfer integrals (transport properties)¶
ADF can provide input parameters, such as charge transfer integrals, that are needed in approximate methods that model charge transport properties. ADF has the unique feature that it can (also) calculate such transfer integrals based on the direct method by the use of its unique fragment approach.
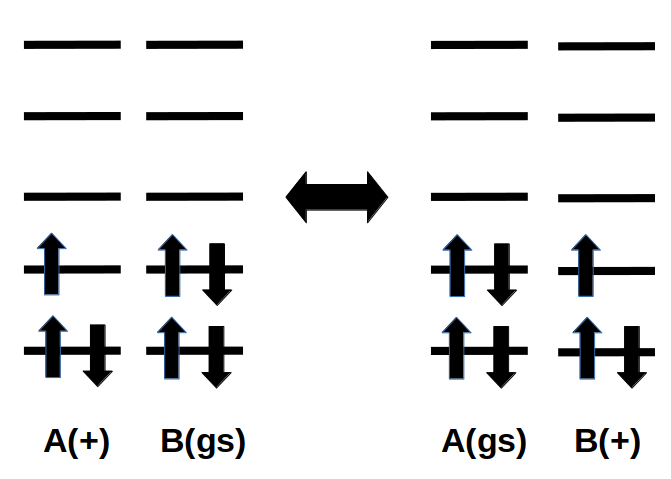
Example electron configuration for charge hopping from A to B or back, where A and B are nearby molecules, or different parts of a complex AB. The hopping can occur from the diabatic state where A is charged and B is in the ground state to the diabatic state where A is in the ground state and B is charged (or back).
In theoretical models of charge transport in organic materials, see Refs. [6] [7] [8], the whole system is divided into fragments, in which an electron or hole is localized on a fragment, and can hop from one fragment to another. In the tight-binding approximation that is used in these models the electron or hole is approximated with a single orbital, and it is assumed that only the nearest neighboring fragments can couple. The models require accurate values of electronic couplings for charge transfer (also referred to as charge transfer integrals or hopping matrix elements) and site energies (energy of a charge when it is localized at a particular molecule) as a function of the geometric conformation of adjacent molecules. Charge transfer integrals for hole transport can be calculated from the energetic splitting of the two highest-occupied molecular orbitals (HOMO and HOMO-1) in a system consisting of two adjacent molecules, also called “energy splitting in dimer” (ESID) method. For electron transport these can be calculated from the two lowest-unoccupied orbitals (LUMO and LUMO+1) in this ESID method. ADF can also calculate transfer integrals based on the direct method by the use of its unique fragment approach. see Refs. [7] [8]. ADF allows one to use molecular orbitals on individual molecules as a basis set in calculations on a system composed of two or more molecules. The charge transfer integrals obtained in this way differ significantly from values estimated from the energy splitting between the highest occupied molecular orbitals in a dimer. The difference is due to the nonzero spatial overlap between the molecular orbitals on adjacent molecules. Also, ADF’s methods are applicable in cases where an orbital on one molecule couples with two or more orbitals on another molecule.
Charge transfer integrals with the TRANSFERINTEGRALS key¶
In this method the matrix elements of the molecular Kohn-Sham Hamiltonian \(H^{KS}\) in the basis of fragment orbitals is used to calculate site energies and charge transfer integrals. Likewise the overlap integrals between fragment orbitals are calculated. No explicit electrons are removed or added in this method. For electron mobility calculations the fragment LUMO’s are considered. For hole mobility calculations the fragment HOMO’s are considered.
To calculate the charge transfer integrals, spatial overlap integrals and site energies, include the key TRANSFERINTEGRALS in the input for ADF. Symmetry NOSYM should be used. The molecular system typically should be build from 2 fragments. In the fragment calculation full symmetry can be used.
TRANSFERINTEGRALS
Symmetry NOSYM
Fragments
frag1 frag1.results/adf.rkf
frag2 frag2.results/adf.rkf
End
By default, integrals are calculated only for the HOMO (LUMO) of the fragments, and possibly HOMO-1, HOMO-2 (LUMO+1, LUMO+2) if the energy of those fragment orbitals are close to the HOMO (LUMO) of that fragment. To calculate the matrix elements and overlap integrals based on all fragment orbitals one can use the key:
PRINT FMATSFO
The method described here to calculate charge transfer integrals is more approximate than the next method that uses FDE. The major difference is how effects of a localized charge are included.
If 2 fragments are used the electronic coupling V (also known as effective (generalized) transfer integrals J_eff) for hole transfer or electron transfer is calculated as V = (J-S(e1+e2)/2)/(1-S^2). Here e1, e2, are the site energies of fragment 1 and 2, respectively. J is the charge transfer integral, and S the overlap integral.
In case of electron mobility calculations \(\phi_1\) is the LUMO of fragment 1 and \(\phi_2\) is the LUMO of fragment 2. In case of hole mobility calculations \(\phi_1\) is the HOMO of fragment 1 and \(\phi_2\) is the HOMO of fragment 2. The electronic coupling between the HOMO of the donor fragment and the LUMO of the acceptor fragment and vice-versa is also calculated, which represent the probability of a charge recombination process.
If there is (near) degeneracy in the fragment HOMO and/or LUMO multiple electronic couplings \(V_i\) are printed. A total electronic coupling is calculated as
TIDegeneracyThreshold float
TIDegeneracyThreshold- Type:
Float
- Default value:
0.1
- Unit:
eV
- Description:
If the orbital energy of the fragment MO is within this threshold with fragment HOMO or LUMO energy, then this fragment MO is included in the calculation of the transfer integrals. Relevant in case there is (near) degeneracy.
Charge transfer integrals with FDE¶
Overview
The ELECTRONTRANSFER keyblock invokes the calculation of Hamiltonian (site energies and couplings) and overlap matrix elements with FDE-derived localized states. Two FDE calculations are (not strictly) needed before running the ELECTRONTRANSFER calculation. The calculated matrix elements are theoretically similar to the ones obtained with the TRANSFERINTEGRALS keyword. A recent review casts ELECTRONTRANSFER in the state-of-the-art of methods for computing charge transfer couplings, and provides a step-by-step guide for computing such couplings with ADF [1].
Features
Effects of orbitals relaxation due to localized charges, Refs. [9] [2].
Effects of polarization due to molecules in the environment, Ref. [2].
ELECTRONTRANSFER is linear scaling in the number of fragments when the system is composed by more than one fragment.
The code can tackle hole transfer, electron transfer, charge separation and charge recombination processes [3].
Can compute transfer integrals from diabats obtained with the Constrained DFT method (i.e., invoked by using the experimental CDFT keyword of ADF). This includes calculation of couplings between diabats made of a single fragment.
It is possible to include the effect of the environment on CDFT diabats by coupling it with an FDE calculation [4].
The performance of ElectronTransfer in the evaluation of the hole transfer coupling, was benchmarked against wave functions methods, with an error below 7%. PBE, PW91, B3LYP and PBE0 functionals, with PW91k for the non-additive component of the kinetic energy and TZP basis function, are recommended to obtain the FDE-derived localized states [5].
The code was parallelized in ADF2018.
Limitations
Hybrid functionals are not yet supported
adf.rkf (TAPE21) files with charge or spin-localized states with specific names are needed
These two limitations do not apply to the method with the TRANSFERINTEGRALS key, but the TRANSFERINTEGRALS has many other limitations. Like the method with the TRANSFERINTEGRALS key fragments are needed.
ELECTRONTRANSFER input
The minimum input for the ELECTRONTRANSFER key is:
FRAGMENTS
frag1 FragFile1
...
fragN FragFileN
END
ELECTRONTRANSFER
NumFrag N
END
where frag1 … fragN are the labels of the fragments in the calculation, and FragFile1 … FragFileN are the adf.rkf (TAPE21) files of spin RESTRICTED calculations of the isolated fragments, N is the total number of fragments employed in the calculation.
Files and file names
The fragment files to be used in the ELECTRONTRANSFER calculation are generally different from the adf.rkf (TAPE21) files used in the FRAGMENTS key block. Two types of fragment adf.rkf (TAPE21) files are needed by the calculation:
The isolated closed-shell TAPE files for the FRAGMENTS keyblock
The adf.rkf (TAPE21) files of the charge or spin localized states (which can be obtained with an FDE calculation as done in the example below)
There are 2 charge localized states. They are labeled with A and B. The respective adf.rkf (TAPE21) files must be names as follows:
fragA1.t21, fragA2.t21, ... , fragAN.t21 (for state A)
fragB1.t21, fragB2.t21, ... , fragBN.t21 (for state B)
The above files should be copied to the working folder of the ADF calculation prior to executing ADF.
Options
ELECTRONTRANSFER
NumFrag N
{Joint|Disjoint}
{Debug}
{Print EIGS|SAB}
{FDE}
{INVTHR threshold}
{CDFT}
{KNADD}
END
Joint|DisjointThe default is “Joint”. Joint is always recommended. The “Disjoint” formalism is described in Ref. [2] and is much faster than the “Joint” formalism when more than 2 fragments are considered. Joint and Disjoint are equivalent for systems composed of only 2 fragments. Disjoint should only be used if the fragment files are obtained in an FDE calculation (see FDE below).
DebugThe code performs additional checks (determinants, diagonalizations, inversions, traces, etc.). Substantial increase in the output should be expected.
PrintIf EIGS, it will print the (unformatted) matrix of the MO coefficient in the AO representation. If SAB, it will print the (unformatted) matrix of the diagonal and transition overlap matrix in the MO representation.
FDEAn FDE calculation including more than 2 fragments must include the following key block:
ELECTRONTRANSFER FDE END
and the numerical integration precision in the last FDE calculation for every subsystem should be set to no less than:
BeckeGrid Quality Good End
if in the subsequent ELECTRONTRANSFER calculation the DISJOINT subkey is used.
Invthr thresholdDefault 1.0e-3, is a threshold for the Penrose inversion of the transition overlap matrix. If warnings about density fitting are printed, invthr may be increased up to 1.0e-2. Larger invthr might affect the quality of the calculated couplings and excitation energies.
CDFTIf disjoint is selected, this keyword must be selected if the evaluation of the electronic coupling is sought between diabats located on the same CDFT fragment. In this case, the CDFT fragment has to be always first under the ATOMS keyword.
KNADDIf disjoint is selected, this allows the kinetic energy of each fragment to be obtained locally without using the full grid. This keyword is recommended when there are many tens of subsystems, such as systems with several solvent molecules.
Output
The output of the example in $AMSHOME/examples/adf/ElectronTransfer_FDE_H2O is discussed here. This example involves the calculation of electronic coupling, site energies and charge-transfer excitation energy for the hole transfer in a water dimer.
============ Electron Transfer RESULTS ===================
Electronic Coupling = 0.000000 eV
Electronic Coupling = -0.003569 cm-1
H11-H22 = -1.396546 eV
Excitation Energy = 1.396546 eV
Overlap = 0.000000
H11 H22 H12 = -152.443000816341 -152.391678701092 -151.743979368040 Eh
S11 S22 S12 = 0.981795415192 0.981006454450 -0.000000023700
=========== END Electron Transfer RESULTS ================
Due to symmetry, the overlap is almost diagonal (Overlap = 0.00), thus the transition density is evaluated with one less electron as explained in Ref. [2].
The electronic coupling between the state with a positive charge localized on one water molecule and another with the charge localized on the other water molecule is given by “Electronic Coupling” and is reported in eV and cm^-1.
“H11-H22” is the difference of the site energies in eV. Values of the site energies are given by the first two values of “H11 H22 H12” in atomic units.
“Excitation Energy” reports the value of the transfer excitation energy as calculated by diagonalization of the 2X2 generalized eigenvalue problem in the basis of the charge-localized states, see Refs. [2] [9].
“S11 S22 S12” are the values of the non-normalized overlaps.
Charge transfer integrals with FOCDFT¶
FOCDFT can be used to calculate charge transfer integrals. FOCDFT is a fragment orbital based method for constraining (integer) charges and spins on fragments. It uses the (localized) Lowdins that ADF makes to to constrain charges and spins on fragments. This method can be used to specify 2 different electron configurations of the same complex, such that a charge on the first fragment in the first calculation is transferred to the second fragment in the second calculation.
The 2 electron configurations calculated with FOCDFT will lead to 2 1-determinantal wave functions with occupied orbitals, which are not necessarily mutually orthonormal. Löwdin’s pairing theorem (see for example Ref. [10]) is used to make set a set of occupied orbitals that are orthonormalized and ‘paired’, and which do not change the resulting 2 1-determinantal wave functions. Because FOCDFT uses the (localized) Lowdins that ADF makes, and charge is transferred from 1 fragment to the other, the 2 1-determinantal wave functions are orthonormal and there is at least 1 pair of ‘corresponding orbitals’ that have zero overlap. These two ‘corresponding orbitals’ \(a_i\) (of the first calculation) and \(b_i\) (of the second calculation) are used to calculate an approximation to the electronic coupling by calculating
where \(F^{A}\) is the Fock matrix in the first calculation and \(F^B\) is the off-diagonal Fock matrix in the second calculation. The off-diagonal Fock matrix is the off-diagonal part of the Fock matrix between Lowdins on the first fragment and Lowdins on the second fragment, before it is set to zero in FOCDFT. The overlap of the other paired orbitals is taken into account in the final electronic coupling.
In FOCDFT electrontransfer effects of orbital relaxation due to localized charges are included and effects of polarization due to molecules in the environment can be included. FOCDFT electrontransfer can tackle hole transfer and electron transfer. Hybrid functionals are supported. FOCDFT electrontransfer is not benchmarked against wave functions methods.
For the calculation of electronic couplings between locally excited states and charge separated states see the section on exciton transfer integrals with FOCDFT.
With the proper input ADF will do the 2 FOCDFT calculations on the 2 diabatic states on the same complex consecutively and print the site energies and electronic coupling to output. In case of hole charge transfer in the ADF part of the input one should use something like:
fragments
Frag1 Frag1.results/adf.rkf
Frag2 Frag2.results/adf.rkf
end
spinpolarization 1
unrestricted
FOCDFT
charge 1 0
spinpolarization 1 0
electrontransfer
charge 0 1
spinpolarization 0 1
end
end
The FOCDFT and FOCDFT%ElectronTransfer keys in more detail:
FOCDFT
Charge float_list
SpinPolarization float_list
ElectronTransfer
Charge float_list
OffDiagonalHF Yes/No
OffDiagonalHFValue float
SpinPolarization float_list
End
End
FOCDFT- Type:
Block
- Description:
Localize orbitals on fragments and constrain charge and spin polarization on fragments.
Charge- Type:
Float List
- Description:
Constrain charge on fragments. Number of charges should be the same as number of fragments, and sum should add up to total charge.
SpinPolarization- Type:
Float List
- Description:
Constrain spin polarization on fragments. Number of spin polarization values should be the same as number of fragments, and sum should add up to total spin polarization. Calculation should be spin unrestricted.
ElectronTransfer- Type:
Block
- Description:
Charge- Type:
Float List
- Description:
Constrain charge on fragments for the second calculation. Number of charges should be the same as number of fragments, and sum should add up to total charge.
OffDiagonalHF- Type:
Bool
- Default value:
No
- GUI name:
Off diagonal HF
- Description:
Off diagonal HF matrix elements.
OffDiagonalHFValue- Type:
Float
- Default value:
1.0
- GUI name:
Off diagonal HF value
- Description:
Amount of HF in case off diagonal HF matrix elements.
SpinPolarization- Type:
Float List
- Description:
Constrain spin polarization on fragments for the second calculation. Number of spin polarization values should be the same as number of fragments, and sum should add up to total spin polarization. Calculation should be spin unrestricted.
References