GREEN: Non-self-consistent Green’s function calculation¶
green is an auxiliary program which can be used to calculate the density of states (DOS) and transmission of molecules connected to semi-infinite contacts. The transmission is the electron transmission through a molecule connected to semi-infinite contacts. The calculation is based on the non-self-consistent Green’s function method, which is an approximation to the non-equilibrium Green’s function (NEGF) method. The details of this method can be found in chapter 2 and appendix C of the PhD thesis of Jos Seldenthuis (2011). See Ref. [1] for more details on the applicability of the wide-band limit approximation. Suggestion is to consider to use NEGF implementation in the periodic program BAND program, see the BAND manual, since it might give better results.
Introduction¶
The utility program green calculates the density of states (DOS) and zero-bias transmission of molecule connected to two semi-infinite contacts. A typical calculation consists of two parts. The first is the calculation of the effect of the semi-infinite contacts, contained in the so-called self-energy matrix. The second is the calculation of the desired properties of the molecule with the self-energies.
Self-energy
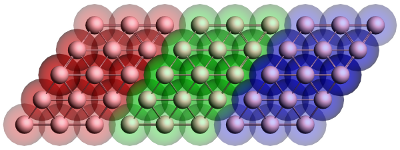
Figure 1: Geometry of the gold contact used in the calculation of the self-energy. The lead consists of two surface layers, left (red) and right (blue), and a bulk layer (green). Each principal layer in turn consists of three atomic layers. This should be sufficient to ensure that the Hamiltonian of the central (green) layer is a bulk Hamiltonian.
Since the contacts are semi-infinite, the calculation of their self-energy is effectively a bulk calculation. Since ADF only works with systems of finite size, approximations have to be made. Fig. 1 shows the typical geometry used in the calculation of a gold contact. The geometry consists of three parts, the so-called principal layers. These layers should be large enough that the atoms on one side are not influenced by whatever is attached to the other side. Three atomic layers usually suffice. The green region is the bulk layer. The red and blue regions are the surface layers. Note that the blue region corresponds to the left contact of a molecule and the red region to the right contact.
To calculate the self-energy, we first need to do a single-point calculation of a principal layer. This layer is then used as a fragment in the following calculations. Note that all ADF calculations have to be performed with SYMMETRY NOSYM. We then build up the contact geometry from three copies of the layer fragment as in Fig. 1 and perform another single-point calculation. This results in a Hamiltonian describing the three contact layers and the coupling between them.
From the adf.rkf (TAPE21) file green can now calculate the self-energy matrices with the SURFACE key. This has to be done once for every energy for which we want to calculate the DOS or transmission. For the left contact of the molecule, green needs the blue and green fragments. The self-energy is calculated by taking the (blue) surface layer and iteratively adding more (green) bulk layers until matrices converge to the semi-infinite result. The self-energy of the right contact is similarly calculated from the red and green fragments. Since the self-energy described the effect of an infinite chain of (green) bulk regions on a (red or blue) surface layer, this calculation does not depend on whatever is attached to the contacts. The self-energy matrices can therefore be reused for different molecules.
DOS and transmission

Figure 2: Geometry of the extended molecule used in the calculation of a benzenedithiol junction. The molecule is shown in green, while the left and right contact regions are shown in red and blue, respectively. Note that the red region corresponds to the blue surface layer in Figure 1 and vice versa.
Once the self-energy matrices have been calculated for the desired energies, we can compute the DOS and transmission of a molecule. However, since the self-energy matrices couple to the surface layers of the contacts, we need to include those surface layers in the calculation of the molecule (see Fig. 2). We therefore first perform a single-point calculation with ADF of the isolated molecule. The result is then used as a fragment and combined with the fragments of the surface layers to construct the so-called extended molecule. We then perform another single-point calculation of the final geometry.
From the self-energies of the contacts and the adf.rkf file of the extended molecule, green can now compute the DOS and transmission. This calculation is non-self-consistent since the ADF calculations are all performed on finite instead of semi-infinite systems. This will result in certain artifacts in the DOS and transmission spectra, but those can be made arbitrarily small by choosing the principal layers large enough.
Wide-band-limit¶
In the wide-band limit (WBL) the coupling to the leads is assumed to be independent of energy. Therefore one does not need to calculate any self-energies. This also means that the eigenspace of the Green’s function is independent of energy. It can therefore be diagonalized in advance, greatly speeding up the calculation of the DOS and the transmission. See Ref. [1] for more details on the applicability of the wide-band limit in DFT-based molecular transport calculations.
In the example $AMSHOME/examples/adf/green_Al/green_WBL.run of green, the transmission of benzenedithiol junction in the wide-band limit (WBL) is calculated. In order to model the molecule-metal interface, we do need to include a few gold layers in the calculation. However, unlike before, only a single atomic layer as the principal layer is used. Because a single atomic layer is an unnatural configuration for gold, a minor amount of smearing is necessary to make the calculation converge. The molecule is sandwiched in between the electrodes just like before (see Fig. 2 in the example for benzenedithiol). However, this time each atomic layer of gold gets its own fragment. The reason for this configuration is that if the WBL is used on the entire gold contact the result is an an unphysical coupling to the leads; even the gold atoms contacting the molecule would have a direct coupling to the environment. A much better result can be obtained by only using the WBL on the back-most atomic layer and letting the electrons propagate naturally through the rest of the contact. Because the WBL is computationally so inexpensive, we can easily calculate the DOS and transmission for 10,000 points instead of 1000.
A comparison of the resulting transmission with the calculation with self-energies is shown in the following figure:

The WBL shows good agreement with the non-WBL transmission around the Fermi energy (-0.195 Hartree or -5.306 eV). Note that the quality of the WBL depends on the choice of the coupling (ETA). For this particular contact geometry we obtain good agreement for ETA = 0.02 Hartree, but a better value may be found for other electrodes. Finally, the WBL can be incrementally improved by adding more gold layers to the extended molecule. For many layers it converges to the calculation with full self-energies.
Input options¶
The input for green is keyword oriented and is read from the standard input. green is typically first used to calculate the self-energy matrices of the left and right contacts (with the SURFACE key), and then to calculate the density of states (DOS) and transmission (with the DOS and TRANS keys, respectively), using those self-energies. The only keyword required to be present in all calculations is the EPS keyword, which specifies the energy range.
$AMSBIN/green << eor
EPS mineps maxeps numeps
{ETA eta}
{SO sh sl {moc}}
{SURFACE filename
FRAGMENTS f1 f2
END}
{DOS filename}
{TRANS
LEFT filename
FRAGMENT fragment
ETA eta
END
RIGHT filename
FRAGMENT fragment
ETA eta
END}
eor
EPS mineps maxeps numepsThe energy range for which either the self-energy matrices or the DOS and transmission have to be calculated. The range consists of numeps ( \(\leq\) 1) points running from mineps to maxeps inclusive.
(optional) ETA etaThe imaginary energy, or the distance from the real axis, in the calculation of the Green’s function. The value needs to be a small positive number to prevent singularities in the calculation. The default value (10-6 Hartree) is sufficient for most calculations.
(optional) SO sh sl {moc}The shifts for the scissors operator. All occupied orbitals (HOMO and below) are shifted by sh, while the unoccupied orbitals (LUMO and above) are shifted by sl. Orbitals are considered occupied if their (possibly fractional) occupation is larger than moc (default 0). The scissor operator can partially remedy the underestimation of the HOMO-LUMO gap in DFT. The sh and sl shifts generally have the same magnitude, but opposite sign (with sh usually being negative and sl positive). A good estimate for the magnitude is the sum of the ionization potential and the energy of the HOMO of the free molecule. This can be improved by including image charge effects. For more details, see Ref. [2]. By default, sh=sl=0.
(optional) SURFACESURFACE filename FRAGMENTS f1 f2 END
The SURFACE block key enables the calculation of the self-energy matrices. The filename specifies the adf.rkf file resulting from an ADF calculation of the contacts. This calculation has to be performed with SYMMETRY NOSYM. The FRAGMENTS key is used to specify the two principal layers between which the surface is defined. The resulting self-energy matrices (one for every energy point given by EPS) is stored in a binary KF file named SURFACE.
(optional) DOS filenameThe DOS key enables the calculation of the density of states. The filename specifies the adf.rkf file containing the result of an ADF calculation of the extended molecule (performed with SYMMETRY NOSYM). Two text files will be generated: DOS_A and DOS_B, containing, respectively, the DOS of the spin-A and spin-B electrons. In the case of a spin-unrestricted calculation, DOS_A and DOS_B might differ. If only the DOS of the spin-A electrons is required, the calculation can be sped up by specifying NOSAVE DOS_B. The DOS key requires the presence of the LEFT and RIGHT keys.
(optional) TRANSThe TRANS key enables the calculation of the transmission. The filename specifies the adf.rkf file containing the result of an ADF calculation of the extended molecule (performed with SYMMETRY NOSYM). Two text files will be generated: TRANS_A and TRANS_B, containing, respectively, the transmission of the spin-A and spin-B electrons. In the case of a spin-unrestricted calculation, TRANS_A and TRANS_B might differ. If only the transmission of the spin-A electrons is required, the calculation can be sped up by specifying NOSAVE TRANS_B. The TRANS key requires the presence of the LEFT and RIGHT keys.
LEFT/RIGHTLEFT filename FRAGMENT fragment ETA eta END
The LEFT and RIGHT block keys specify the left and right self-energies used in a calculation of the DOS and transmission. If a filename is specified, the self-energy matrices are read from that file. The energy range of the self-energies has to be consistent with the range specified by the EPS keyword. The FRAGMENT key is used to denote the fragment in the extended molecule (given by the argument to the DOS or TRANS key) to which the self-energy couples. If no filename is specified, the wide-band limit is used. The ETA key can then be used to specify the magnitude of the coupling (10-3 Hartree by default).
Output¶
After a successful calculation of the self-energy matrices, green produces a binary KF file named SURFACE containing two sections. The Surface section contains the energy range:
contents of Surface |
comments |
mineps |
start of the energy range |
maxeps |
end of the energy range |
numeps |
number of points |
The Sigma section contains the real and imaginary parts of the self-energy matrices:
contents of Sigma |
comments |
nfo |
number of fragment orbitals (dimension of the self-energy matrices) |
Re(Sigma_%d) |
the real part of the %d self-energy matrix (numbered from 1 up to numeps) |
Im(Sigma_%d) |
the imaginary part of the %d self-energy matrix (numbered from 1 up to numeps) |
A successful calculation of the density of states (DOS) or transmission results in the text files DOS_A and DOS_B, and TRANS_A and TRANS_B, respectively. The suffixes _A and _B denote the different spins. The text files the DOS and transmission for every energy point and can be plotted with, for example, gnuplot.
GREEN with ADF-GUI¶
In ADF2017 the ADF-GUI can be used to setup a GREEN calculation, and look at the results. Note, however, that not all GREEN options are supported with the ADF-GUI. For example, one can not use unrestricted or wide-band-limit calculations with the ADF-GUI. GUI tutorials exist for NEGF with DFTB or BAND. Suggestion is to consider to use NEGF implementation in the periodic program BAND program, see the BAND manual, since it might give better results.
References