Example: Gold electrodes¶
In this example of green, the self-energies are calculated of gold electrodes, the material most often used in molecular electronics. In the example for the Benzenedithiol junction these self-energies will be used to calculate the DOS and transmission of a benzenedithiol junction. The geometry of the electrodes is shown in Fig. 1.
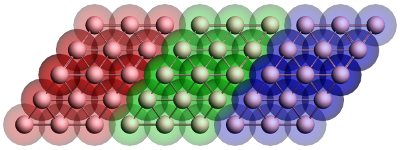
Figure 1: Geometry of the gold contact used in the calculation of the self-energy. The lead consists of two surface layers, left (red) and right (blue), and a bulk layer (green). Each principal layer in turn consists of three atomic layers. This should be sufficient to ensure that the Hamiltonian of the central (green) layer is a bulk Hamiltonian.
The final results are shown in the following figure:
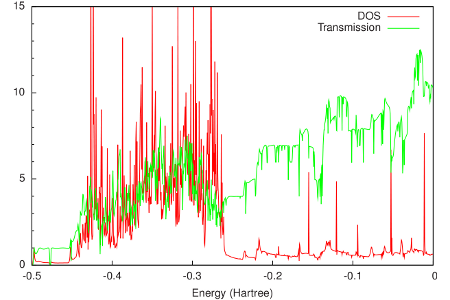
From this figure it can be seen that around the Fermi energy (-0.2 Hartree), both the DOS and the transmission of gold are relatively constant. This feature makes gold an attractive material for electrodes, since one can expect that the transmission of a molecular junction will be dominated by the molecular properties.
#!/bin/sh
# In this example of green, the self-energies are calculated of gold electrodes,
# the material most often used in molecular electronics.
# In the example for the Benzenedithiol junction, green_BDT.run, these self-energies
# will be used to calculate the DOS and transmission of a benzenedithiol junction.
# Each principal layer contains 3x3x3=27 gold atoms.
# For the calculation of the self-energies three principal layers are needed,
# and therefore 81 gold atoms in total.
# To keep the runtimes manageable it is therefore important to choose the basis set
# as small as possible.
# For transport calculations, a DZ basis with a large frozen core is generally sufficient.
# Unfortunately, even with the largest frozen core (Au.4f),
# the basis set for Au still contains 19 electrons.
# A significant speedup can be obtained by limiting this to 11 electrons
# (only the outer *d* and *s* shells).
# Be advised that even with this reduction the total runtime of calculation can be long.
# To facilitate the calculation of the electrodes,
# first a gold atom fragment will be calculated with the smallest possible basis.
# The sample directory contains the required Au.5p and Au.5p.dirac files.
# Note that for gold relativistic effects are important.
# Therefore Scalar ZORA will be used throughout this example.
cp $AMSHOME/examples/adf/green_Al/Au.5p .
cp $AMSHOME/examples/adf/green_Al/Au.5p.dirac .
$AMSBIN/dirac < Au.5p.dirac
mv TAPE12 t12.rel
AMS_JOBNAME=Au $AMSBIN/ams <<eor
System
Atoms
Au 0.0 0.0 0.0
End
end
Task SinglePoint
Engine ADF
corepotentials t12.rel
end
create Au file=Au.5p
relativity
level scalar
formalism ZORA
end
xc
lda SCF VWN
end
EndEngine
eor
# A principal layer of gold consists of three atomic layers,
# which should be sufficient due to the small screening length.
# An atomic layer contains 3x3=9 atoms in a (111) FCC configuration.
# This allows one to use the top-, bride-, and hollow-site binding configurations for a molecule.
# For the following calculations it is necessary to first construct a fragment
# of a principal layer.
AMS_JOBNAME=layer $AMSBIN/ams <<eor
System
atoms
Au -2.355588 -6.662612 0.000000
Au -2.355589 -4.164133 -1.442498
Au -2.355589 -4.164133 1.442498
Au -2.355589 -1.665653 -2.884996
Au -2.355589 -1.665653 0.000000
Au -2.355589 -1.665653 2.884996
Au -2.355589 0.832826 -1.442498
Au -2.355589 0.832826 1.442498
Au -2.355589 3.331306 0.000000
Au 0.000000 -4.996959 0.000000
Au 0.000000 -2.498480 -1.442498
Au 0.000000 -2.498480 1.442498
Au 0.000000 0.000000 -2.884996
Au 0.000000 0.000000 0.000000
Au 0.000000 0.000000 2.884996
Au 0.000000 2.498480 -1.442498
Au 0.000000 2.498480 1.442498
Au 0.000000 4.996959 0.000000
Au 2.355589 -3.331306 0.000000
Au 2.355589 -0.832826 -1.442498
Au 2.355589 -0.832826 1.442498
Au 2.355589 1.665653 -2.884996
Au 2.355589 1.665653 0.000000
Au 2.355589 1.665653 2.884996
Au 2.355589 4.164133 -1.442498
Au 2.355589 4.164133 1.442498
Au 2.355588 6.662612 0.000000
end
end
Task SinglePoint
Engine ADF
fragments
Au Au.results/adf.rkf
end
relativity
level scalar
formalism ZORA
end
symmetry NOSYM
title Principal layer
xc
lda SCF VWN
end
EndEngine
eor
# Three principal layers are stacked together to calculate the self-energies (see Fig. 1).
# The names of the fragments are significant, since one needs to refer to them by name in
# the calculation of the self-energies.
AMS_JOBNAME=bulk $AMSBIN/ams <<eor
System
atoms
Au -9.422355 -11.659571 0.000000 adf.f=left
Au -9.422356 -9.161092 -1.442498 adf.f=left
Au -9.422356 -9.161092 1.442498 adf.f=left
Au -9.422356 -6.662612 -2.884996 adf.f=left
Au -9.422356 -6.662612 0.000000 adf.f=left
Au -9.422356 -6.662612 2.884996 adf.f=left
Au -9.422356 -4.164133 -1.442498 adf.f=left
Au -9.422356 -4.164133 1.442498 adf.f=left
Au -9.422356 -1.665653 0.000000 adf.f=left
Au -7.066767 -9.993918 0.000000 adf.f=left
Au -7.066767 -7.495439 -1.442498 adf.f=left
Au -7.066767 -7.495439 1.442498 adf.f=left
Au -7.066767 -4.996959 -2.884996 adf.f=left
Au -7.066767 -4.996959 0.000000 adf.f=left
Au -7.066767 -4.996959 2.884996 adf.f=left
Au -7.066767 -2.498479 -1.442498 adf.f=left
Au -7.066767 -2.498479 1.442498 adf.f=left
Au -7.066767 0.000000 0.000000 adf.f=left
Au -4.711178 -8.328265 0.000000 adf.f=left
Au -4.711178 -5.829785 -1.442498 adf.f=left
Au -4.711178 -5.829785 1.442498 adf.f=left
Au -4.711178 -3.331306 -2.884996 adf.f=left
Au -4.711178 -3.331306 0.000000 adf.f=left
Au -4.711178 -3.331306 2.884996 adf.f=left
Au -4.711178 -0.832826 -1.442498 adf.f=left
Au -4.711178 -0.832826 1.442498 adf.f=left
Au -4.711179 1.665653 0.000000 adf.f=left
Au -2.355588 -6.662612 0.000000 adf.f=center
Au -2.355589 -4.164133 -1.442498 adf.f=center
Au -2.355589 -4.164133 1.442498 adf.f=center
Au -2.355589 -1.665653 -2.884996 adf.f=center
Au -2.355589 -1.665653 0.000000 adf.f=center
Au -2.355589 -1.665653 2.884996 adf.f=center
Au -2.355589 0.832826 -1.442498 adf.f=center
Au -2.355589 0.832826 1.442498 adf.f=center
Au -2.355589 3.331306 0.000000 adf.f=center
Au 0.000000 -4.996959 0.000000 adf.f=center
Au 0.000000 -2.498480 -1.442498 adf.f=center
Au 0.000000 -2.498480 1.442498 adf.f=center
Au 0.000000 0.000000 -2.884996 adf.f=center
Au 0.000000 0.000000 0.000000 adf.f=center
Au 0.000000 0.000000 2.884996 adf.f=center
Au 0.000000 2.498480 -1.442498 adf.f=center
Au 0.000000 2.498480 1.442498 adf.f=center
Au 0.000000 4.996959 0.000000 adf.f=center
Au 2.355589 -3.331306 0.000000 adf.f=center
Au 2.355589 -0.832826 -1.442498 adf.f=center
Au 2.355589 -0.832826 1.442498 adf.f=center
Au 2.355589 1.665653 -2.884996 adf.f=center
Au 2.355589 1.665653 0.000000 adf.f=center
Au 2.355589 1.665653 2.884996 adf.f=center
Au 2.355589 4.164133 -1.442498 adf.f=center
Au 2.355589 4.164133 1.442498 adf.f=center
Au 2.355588 6.662612 0.000000 adf.f=center
Au 4.711179 -1.665653 0.000000 adf.f=right
Au 4.711178 0.832826 -1.442498 adf.f=right
Au 4.711178 0.832826 1.442498 adf.f=right
Au 4.711178 3.331306 -2.884996 adf.f=right
Au 4.711178 3.331306 0.000000 adf.f=right
Au 4.711178 3.331306 2.884996 adf.f=right
Au 4.711178 5.829785 -1.442498 adf.f=right
Au 4.711178 5.829785 1.442498 adf.f=right
Au 4.711178 8.328265 0.000000 adf.f=right
Au 7.066767 0.000000 0.000000 adf.f=right
Au 7.066767 2.498479 -1.442498 adf.f=right
Au 7.066767 2.498479 1.442498 adf.f=right
Au 7.066767 4.996959 -2.884996 adf.f=right
Au 7.066767 4.996959 0.000000 adf.f=right
Au 7.066767 4.996959 2.884996 adf.f=right
Au 7.066767 7.495439 -1.442498 adf.f=right
Au 7.066767 7.495439 1.442498 adf.f=right
Au 7.066767 9.993918 0.000000 adf.f=right
Au 9.422356 1.665653 0.000000 adf.f=right
Au 9.422356 4.164133 -1.442498 adf.f=right
Au 9.422356 4.164133 1.442498 adf.f=right
Au 9.422356 6.662612 -2.884996 adf.f=right
Au 9.422356 6.662612 0.000000 adf.f=right
Au 9.422356 6.662612 2.884996 adf.f=right
Au 9.422356 9.161092 -1.442498 adf.f=right
Au 9.422356 9.161092 1.442498 adf.f=right
Au 9.422355 11.659571 0.000000 adf.f=right
end
end
Task SinglePoint
Engine ADF
fragments
left layer.results/adf.rkf
center layer.results/adf.rkf
right layer.results/adf.rkf
end
relativity
level scalar
formalism ZORA
end
symmetry NOSYM
title Bulk gold
xc
lda SCF VWN
end
EndEngine
eor
# Similar to the other examples, the self-energies of the left and right contacts
# is calculated for 1000 energy points between -0.5 and 0 Hartree.
# This results in two keyfiles of approximately 2.5 GB each.
# Since the self-energies are independent of whatever is placed between the contacts,
# they can be reused many times.
$AMSBIN/green << eor
SURFACE bulk.results/adf.rkf
FRAGMENTS center right
END
EPS -0.5 0 1000
ETA 1e-6
eor
mv SURFACE left.kf
$AMSBIN/green << eor
SURFACE bulk.results/adf.rkf
FRAGMENTS center left
END
EPS -0.5 0 1000
ETA 1e-6
eor
mv SURFACE right.kf
# In order to interpret transmissions calculated with these self-energies,
# it is necessary to know the location of the Fermi energy.
# An estimate for the Fermi energy can be obtained from the bulk SCF calculation
# by taking the average of the HOMO and LUMO energies, which in this case equals -0.195 Hartree.
# Usually the self-energies will be used to calculate the transmission of a molecular junction.
# However, it is instructive to use a principal layer of gold as the "molecule" and study
# the DOS and transmission of bulk gold.
$AMSBIN/green << eor
DOS bulk.results/adf.rkf
TRANS bulk.results/adf.rkf
EPS -0.5 0 1000
ETA 1e-6
LEFT left.kf
FRAGMENT left
END
RIGHT right.kf
FRAGMENT right
END
NOSAVE DOS_B, TRANS_B
eor
echo ""
echo "Contents of DOS_A:"
cat DOS_A
echo "END"
echo ""
echo "Contents of TRANS_A:"
cat TRANS_A
echo "END"