Example: DOS and transmission: Aluminium¶
As an example of a non-self-consistent Green’s function calculation, we will look at the density of states (DOS) and transmission of an infinite 1D chain of Aluminum atoms.
The final resulting DOS and transmission are shown in the following figure:
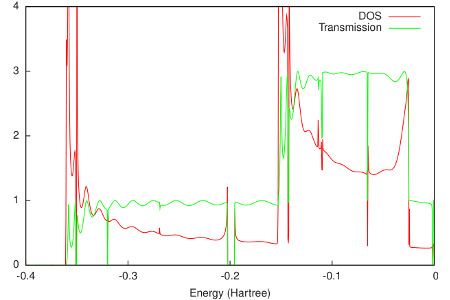
As would be expected for a 1D system, the DOS shows Van Hove singularities at the band edges. Apart from oscillations due to the finite size of the system in ADF, the transmission only reaches integer values. Between approximately -0.35 and -0.15 Hartree, only the sigma channel contributes to the transmission. Above -0.15 Hartree also the two pi channels start to contribute.
#!/bin/sh
# As an example of a non-self-consistent Green's function calculation, we will
# look at the density of states (DOS) and transmission of an infinite 1D chain
# of Aluminum atoms.
# First we need to perform a single-point calculation with ADF on a principal
# layer, consisting, in this case, of four atoms. Since bulk Aluminum has an FCC
# structure with a lattice constant of 4.05 Angstrom, the nearest neighbor
# distance is approximately 2.83 Angstrom. green requires SYMMETRY NOSYM, so we
# have the following input file for the principal layer:
AMS_JOBNAME=layer $AMSBIN/ams <<eor
System
atoms
Al -4.290000 0.000000 0.000000
Al -1.430000 0.000000 0.000000
Al 1.430000 0.000000 0.000000
Al 4.290000 0.000000 0.000000
end
end
Task SinglePoint
Engine ADF
basis
core Large
type DZP
end
scf
converge 1.0e-8
end
symmetry NOSYM
title Principal layer
xc
lda SCF VWN
end
EndEngine
eor
# The bulk contact geometry consists of three principal layers:
AMS_JOBNAME=bulk $AMSBIN/ams <<eor
System
atoms
Al -15.730000 0.000000 0.000000 adf.f=left
Al -12.870000 0.000000 0.000000 adf.f=left
Al -10.010000 0.000000 0.000000 adf.f=left
Al -7.150000 0.000000 0.000000 adf.f=left
Al -4.290000 0.000000 0.000000 adf.f=center
Al -1.430000 0.000000 0.000000 adf.f=center
Al 1.430000 0.000000 0.000000 adf.f=center
Al 4.290000 0.000000 0.000000 adf.f=center
Al 7.150000 0.000000 0.000000 adf.f=right
Al 10.010000 0.000000 0.000000 adf.f=right
Al 12.870000 0.000000 0.000000 adf.f=right
Al 15.730000 0.000000 0.000000 adf.f=right
end
end
Task SinglePoint
Engine ADF
fragments
left layer.results/adf.rkf
center layer.results/adf.rkf
right layer.results/adf.rkf
end
scf
accelerationmethod LISTi
converge 1.0e-10
end
symmetry NOSYM
title Bulk
xc
lda SCF VWN
end
EndEngine
eor
# Notice that we have increased the number of SCF iterations. The combination of
# SYMMETRY NOSYM with a 1D chain of metal atoms generally leads to convergence
# problems. This is the main reason why the principal layer consists of only
# four atoms. Fortunately, for larger 3D contacts, the convergence is generally
# better.
# From the bulk TAPE21 file green can calculate the self-energies of the left
# and right contacts. As discussed in the introduction, the self-energy of the
# left contact needs the center and right fragments of the bulk calculation, and
# the self-energy of the right contact needs the center and left fragments.
# Since we need a self-energy matrix for every energy for which we want to
# calculate the DOS and transmission, already here we have to specify the energy
# range. We take 1000 points between -0.4 and 0 Hartree.
$AMSBIN/green <<eor
SURFACE bulk.results/adf.rkf
FRAGMENTS center right
END
EPS -0.4 0 1000
ETA 1e-6
eor
mv SURFACE left.kf
$AMSBIN/green <<eor
SURFACE bulk.results/adf.rkf
FRAGMENTS center left
END
EPS -0.4 0 1000
ETA 1e-6
eor
mv SURFACE right.kf
# Since we want to calculate the DOS and transmission of bare aluminum, we can
# reuse the bulk.t21 file for the extended molecule. We couple the left self-
# energy to the 'left' fragment and the right self-energy to the 'right'
# fragment in bulk.t21. Since we performed restricted ADF calculations, there is
# no difference between spin-A and spin-B and we can omit spin-B from the
# calculation.
$AMSBIN/green <<eor
DOS bulk.results/adf.rkf
TRANS bulk.results/adf.rkf
EPS -0.4 0 1000
ETA 1e-6
LEFT left.kf
FRAGMENT left
END
RIGHT right.kf
FRAGMENT right
END
NOSAVE DOS_B, TRANS_B
eor
# As would be expected for a 1D system, the DOS shows Van Hove singularities at
# the band edges. Apart from oscillations due to the finite size of the system
# in ADF, the transmission only reaches integer values. Between approximately
# -0.35 and -0.15 Hartree, only the sigma channel contributes to the
# transmission. Above -0.15 Hartree also the two pi channels start to
# contribute.
echo ""
echo "Contents of DOS_A:"
cat DOS_A
echo "END"
echo ""
echo "Contents of TRANS_A:"
cat TRANS_A
echo "END"