NMR shifts with relativistic DFT¶

Scalar relativistic and spin-orbit coupled calculations of NMR chemical shifts¶

Scalar relativity and spin-orbit coupling can have a large effect on the calculated NMR parameters, especially for heavy atoms. Relativistic effects can also be significant for a light element that is close to a heavy atom. This tutorial addresses how the NMR chemical shift of ¹H in the hydrogen halides series (HF, HCl, HBr, HI) is affected by spin-orbit coupling. For more information on how relativity effects the calculation of NMR parameters, see Jochen Autschbach‘s chapter on ‘Relativistic Effects on NMR Parameters’ in High Resolution NMR Spectroscopy edited by Rubén Contreras.

In this tutorial, we compare the NMR results with the following two XC functionals: GGA PBE and hybrid PBE0 (recommended). Thus in total 16 calculations will be performed: 4 (molecules HF, HCl, HBr, and HI) times 2 (PBE and PBE0) times 2 (scalar relativistic and spin-orbit coupled). Each of these calculation will have a different optimized geometry.

Geometry optimization and NMR chemical shifts of ¹H in the H-X series¶

First we draw HF and define the settings for a geometry optimization with the PBE functional and the ZORA scalar relativistic Hamiltonian, using an all-electron QZ4P basis set with a ‘Numerical Quality’ good:

1. Start up AMSinput

2. Press ‘h’ to switch to the building mode and click somewhere in the canvas to draw an H atom

3. Press ‘f’ and click somewhere close to the H to attach a fluorine atom to the H. Press ‘Esc’ to exit building mode.

4. Symmetrize the system by clicking on

5. In the ADF Main panel, select the task Geometry Optimization

6. Select the XC functional GGA:PBE

7. Select the QZ4P Basis set

8. Select the Frozen core none

9. Select Numerical quality Good

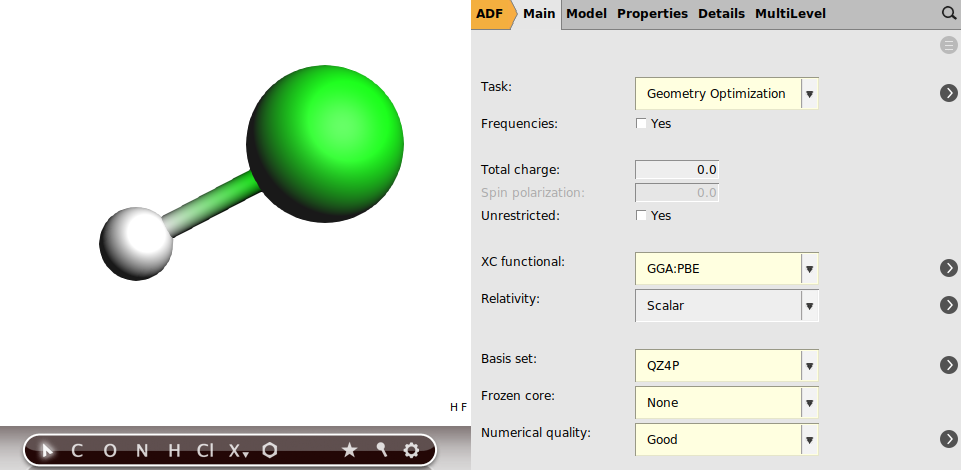
Note that typically for geometry optimizations a TZP or TZ2P basis set is enough. For accurate NMR calculations one should use an all electron basis set on the atoms on which one wants to calculate the NMR parameters. Typically for NMR chemical shifts TZ2P is enough, but if you can afford it one can use QZ4P, like in this case, see the FAQ on recommend settings for NMR calculations.. A numerical quality good is recommended for NMR calculations.

Now we will define the NMR calculation that will be performed after the geometry optimization:

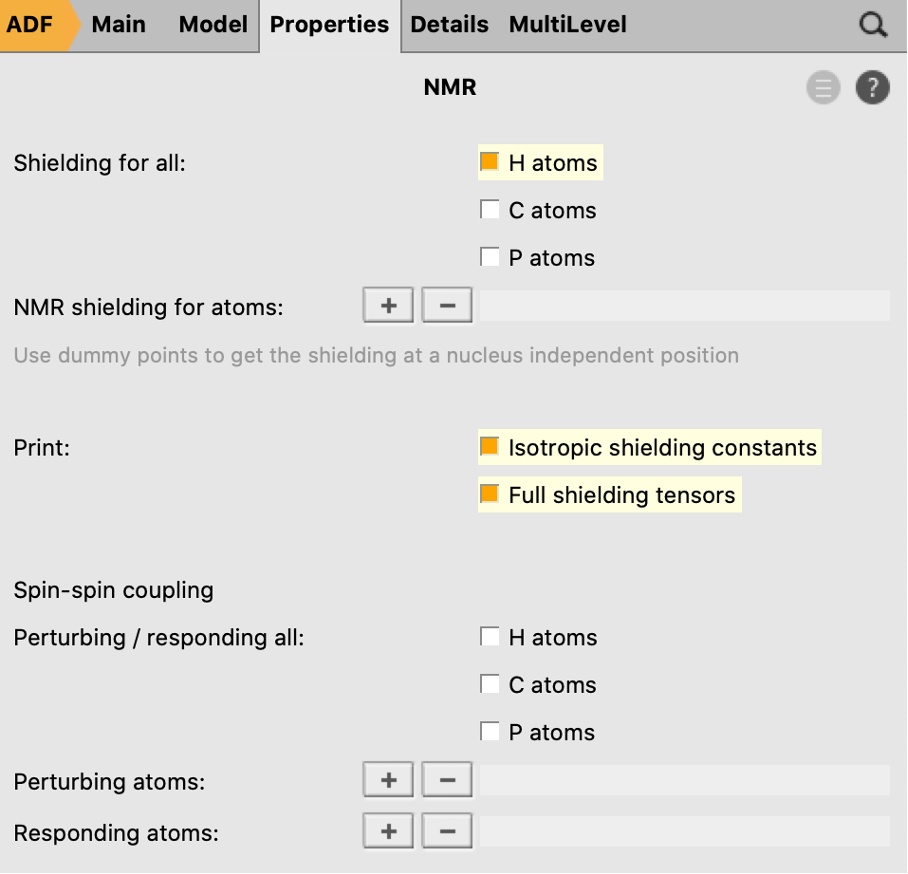
After the calculation is finished, you can look at the results:

You can find here at the bottom the NMR Shielding of 29.15 ppm. The interatomic distance of HF can be found by, at first, reading in the new coordinates and bonds after the geometry optimization. Then, if you select both atoms, H and F, you can read the interatomic distance from the geometry input box on the bottom right. You could also extract the geometric data and NMR shielding in one go by using the ADFreport tool (see below).

Run calculations for the other hydrogen halides¶

Starting from HF, you can go down the periodic table by either making new inputs, or changing the halide:

This will not change the interatomic distance, so it is recommended you pre-optimize before running the DFT calculations. Do not forget to save the new molecule under a different job name. In the same manner, you can replace Cl by Br and then Br by I.

These calculations will take increasingly more time to complete. Collect the distances and NMR Shieldings.

Vary the relativistic approach and density functional (XC)¶

Now we will consider all the remaining combinations of the XC functional and relativistic treatment. The most efficient way to perform these subsequent calculations is to start with the converged geometries for the PBE + SR (scalar-relativistic treatment) and change the XC functional and/or the relativistic treatment.

Make sure you save each new input file under a different name. Thus in total 4 calculations will be performed for each molecule:

• XC functional (GGA:PBE) and Relativity (Scalar) (this calculation was done above)

• XC functional (GGA:PBE) and Relativity (Spin-Orbit)

• XC functional (Hybrid:PBE0) and Relativity (Scalar)

• XC functional (Hybrid:PBE0) and Relativity (Spin-Orbit)

The spin-orbit coupling NMR calculations will warn you that symmetry will be switched off. Click OK to proceed. Hybrid calculations (PBE0) will take longer than GGA calculations (PBE). Spin-orbit calculations will take much longer than scalar relativistic ones.

Analyze multiple jobs with ADFreport¶

If you want to analyze the 16 calculations in one go, you can make use of the AMSreport tool in AMSJobs (the window with your jobs listed):

You will get an html file reporting all distances and NMR chemical shieldings in your default browser.

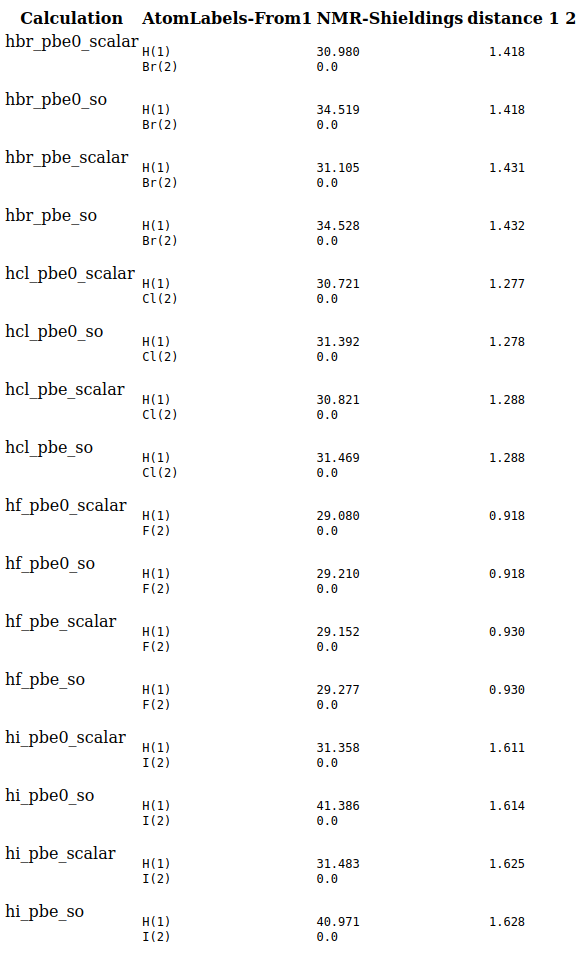
In this report zero’s are shown for the NMR chemical shieldings on the halide atoms that are not calculated.

These calculated numbers can be compared to experimental ones. The experimental values for ¹H NMR chemical shifts δ_i can be found, for example, in the paper by Wolff and Ziegler 1 . The NMR chemical shift δ_i is defined as the difference of the isotropic NMR chemical shielding of a reference compound σ_ref minus that of the interesting compound σ_i:

δ_i = σ_ref - σ_i

In the paper the reference compound is HF, and σ_ref is the isotropic value of the NMR chemical shielding of ¹H in HF (experimentally 28.72 ppm). With this definition of the reference compound the NMR chemical shift of ¹H in HF is 0.0 ppm.

The experimental H-X distances can be found in the NIST Chemistry Webbook , type in the molecular formula and look for the equilibrium distance r_e.

The experimental numbers for the 4 compounds are:

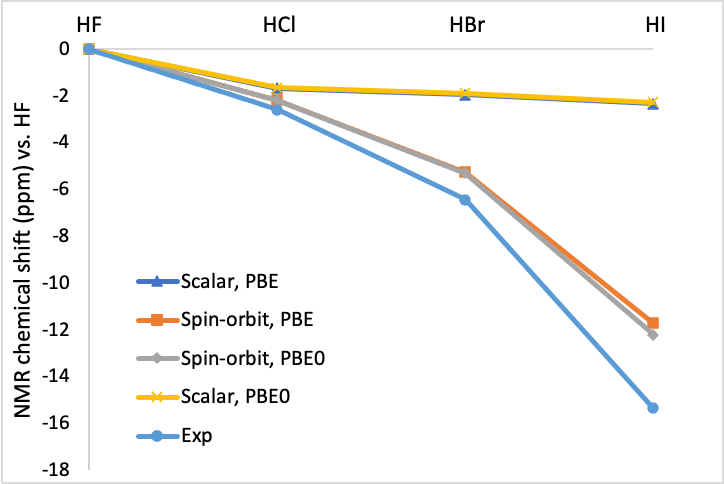
If one compares the optimized geometries with the experimental ones, one can se that they are close. The results with PBE0 are better than with PBE. The effect of spin-orbit coupling on the optimized geometry is small for these closed shell molecules, the largest effect can be seen for HI.

In the next picture the calculated ¹H NMR chemical shifts are compared with the experimental ones. As one can see spin-orbit coupling is needed to get reasonable agreement.

References¶

1

Wolff, S. K., and T. Ziegler. Calculation of DFT-GIAO NMR shifts with the inclusion of spin-orbit coupling. The Journal of chemical physics 109.3 (1998): 895-905.