The right band gaps for the right reason at low computational cost with a Meta-GGA

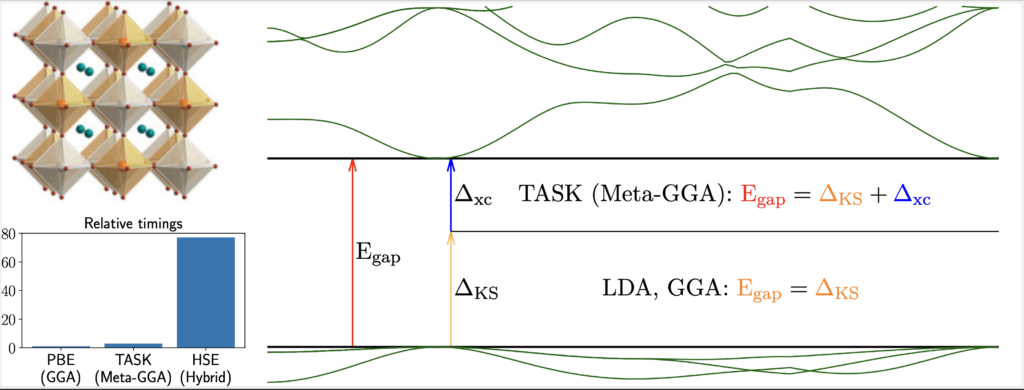
For the discovery of new materials, accurate and fast prediction of the band gap is often important. However, the density functionals that allow for the fastest calculations, LDA and GGA, systematically underestimate the band gap. The fundamental reason for this is that they miss the derivative discontinuity. Therefore, reliable band-gap prediction often resorts to computationally much more expensive hybrid functionals, or beyond-DFT approaches such as GW calculations. However, for materials screening, or for large and complex systems, these methods are often computationally unaffordable.

In a recent study, researchers showed that the Meta-GGA TASK [1] can close this gap between accuracy and computational speed[2]. By comparison of Kohn-Sham and generalized Kohn-Sham calculations, they showed that TASK provides the right band gaps for the right reason. Namely, by a proper combination of contributions from the Kohn-Sham gap ∆KS and the derivative discontinuity ∆xc. Furthermore, even for complex materials like halide perovskites, TASK predicts band gaps similar to those of the hybrid HSE [3]. Especially noteworthy, this accuracy is reached at a fraction of a hybrids computational cost. For band gap calculations within identical settings, numerically stable Meta-GGAs like TASK are typically only three-times more expensive than a GGA, and faster than hybrids by a factor of 20-30.

The Meta-GGA TASK is available directly in AMS and via Libxc. Note that unlike other Meta-GGAs, TASK does not require a radial grid boost. Further, while band gaps are typically calculated within a generalized Kohn- Sham scheme, TASK is also available in the KLI approximation to the OEP since version AMS2023. Lastly, for spin-polarized systems TASK combined with the corrected correlation (CC) functional, also available in AMS and Libxc, is an attractive choice, as tested for molecules [4].

Download three input files for BAND calculations with the TASK Meta-GGA here.

[1] T. Aschebrock, S. Kümmel, Ultranonlocality and accurate band gaps from a meta-generalized gradient approximation, Phys Rev Res. 1, 033082, 2019   https://doi.org/10.1103/PhysRevResearch.1.033082
[2] T. Lebeda, T. Aschebrock, J. Sun, L. Leppert, S. Kümmel, Right band gaps for the right reason at low computational cost with a meta-GGA, Phys Rev Mater. 7, 093803, 2023
https://doi.org/10.1103/PhysRevMaterials.7.093803
[3] J. Heyd, G. E. Scuseria, M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J Chem Phys. 118, 8207 (2003); 124, 219906 (2006). (E).   https://doi.org/10.1063/1.1564060
[4] T. Lebeda, T. Aschebrock, S. Kümmel, First steps towards achieving both ultranonlocality and a reliable description of electronic binding in a meta-generalized gradient approximation, Phys Rev Res. 4, 023061, 2022  https://doi.org/10.1103/PhysRevResearch.4.023061