Closing the band gap of a 2D semiconductor with an electric field
The exercise focusses on a monolayer of Molybdenum disulphide MoS2, because this material is of interest for transistors. In particular the switching to and from a conducting state is of crucial importance. This is based on a CECAM workshop exercise.
Create the MoS2 monolayer
You can use the MoS2 monolayer from our database, see the MoS2 response tutorial. You could also build the crystal from the symmetry information as in the original exercise.
Analyze the DOS and band structure
Tick ‘DOS’ and ‘Bandstructure’. Run the calculation. Switch on Scalar Relativistic as the GUI suggests and then press run again. Open Band Structure from the SCM menu. The bands are not so smooth. Let us make it better. Click on the … next BandStructure and set the interpolation Delta-k to 0.03. Run the calculation and open Band Structure again. The bands should look much more smooth now. If you zoom in and hover over the bands you should see an indirect band gap from the gamma point to the K point, which is on the edge of the Brillouin zone.
Electron/hole transport (advanced)
For semiconductors the shape of the bands near the Fermi level tells you something about how easy the electrons (in the bottom of the conduction band) or holes (in top of the valence band) can move. A small curvature is bad, and a big one is good. The inverse of the curvature is called the effective mass of the electron or hole. To calculate it select Properties → Band Structure → Effective Mass. The result is visible in the raw output in the results section.
Fix the band gap (advanced)
The band gap is about 1.7 eV, whereas experimentally it is 1.8. We have used the LDA functional, which is known to underestimate the gap. You could try to improve the band gap by using a model potential. For systems that are not crystals, the most convenient choice is the GLLB-SC functional. Now the Quasiparticle gap should be a bit higher, since the GLLB-SC includes explicitly the so-called derivative discontinuity.
Applying an electric field
Switch back to the LDA functional an set the electric field (Model → Electric Field) to 3 eV/A. This will reduce the gap significantly. You will need quite strong fields to make the material conducting. You will also find the band character can change a bit at higher fields. The bands are colored according to the main contribution, also known as ‘fat band analysis’.
At what field strength does the material become conducting? Congratulations, you have just switched the device!
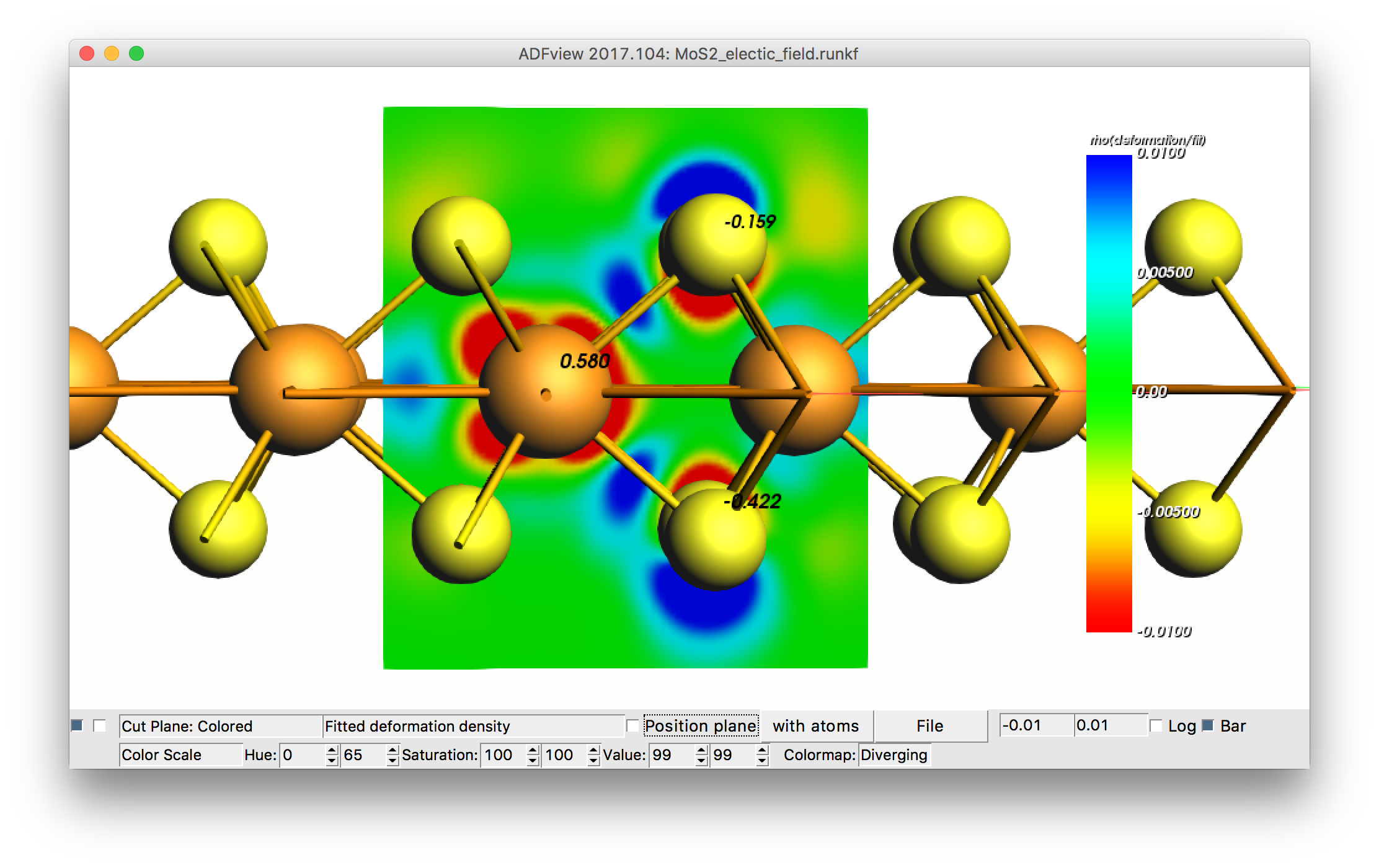
Analyzing the charge
What happens to the charge when you apply an electric field? Open View from the SCM menu. Now select Add → Cut Plane Colored and select at the bottom Fit density → Fitted deformation density. Select the atoms with right click and select Atom info → CM5 Charges.
At a field of 3 eV/A and some tweaking (use a clip plane, fine grid and rainbow map, this picture emerges.
Improving the accuracy
Many aspects influence the results of a calculation. Some are technical, such as the choice of basis set, k-points and integration accuracy; other are theoretical, such as the choice of functional. You can also consider computationally more expensive spin-orbit coupling instead of scalar relativistic. The relativistic effect is small for light atoms and grows with the charge of the nucleus.
The choice of XC functional is not so straightforward. However, to use a GGA is generally better than using the plain LDA. Among the GGAs the PBE functional is a reasonable choice or more modern metaGGAs such as MN15L and SCAN. Finally, the DZ basis set is usually too small, and one should preferably use a TZP one. For the gap (especially when p-electrons are involved) also the spin-orbit might be needed.