Electron and hole mobilities in organic electronics: charge transfer integrals¶
Calculation of charge mobilities¶
Charge mobility is of crucial importance for efficiency in organic electronic devices such as field-effect transistors (OFETs), light-emitting diodes (OLEDs) and photovolatic cells (OPVs). In the so-called hopping regime, charges move incoherently from site to site, with a rate determined by the charge transfer integrals, which are straightforwardly calculated with the unique fragment-based approach in ADF. More approximate charge transfer integrals can be calculated very fast with DFTB.
This guided example explains how to calculate charge mobility with ADF.
Define the fragments for charge transfer¶
As a simple example we will study electron and hole mobility between two naphthalene molecules. Let us start with downloading the .xyz file of the naphthalene dimer, which was cut out from the experimental crystal structure (for your own organic semiconductor material, you can just import the cif file, generate a supercell, and cut out dimers to calculate the charge mobility in different directions). Then:


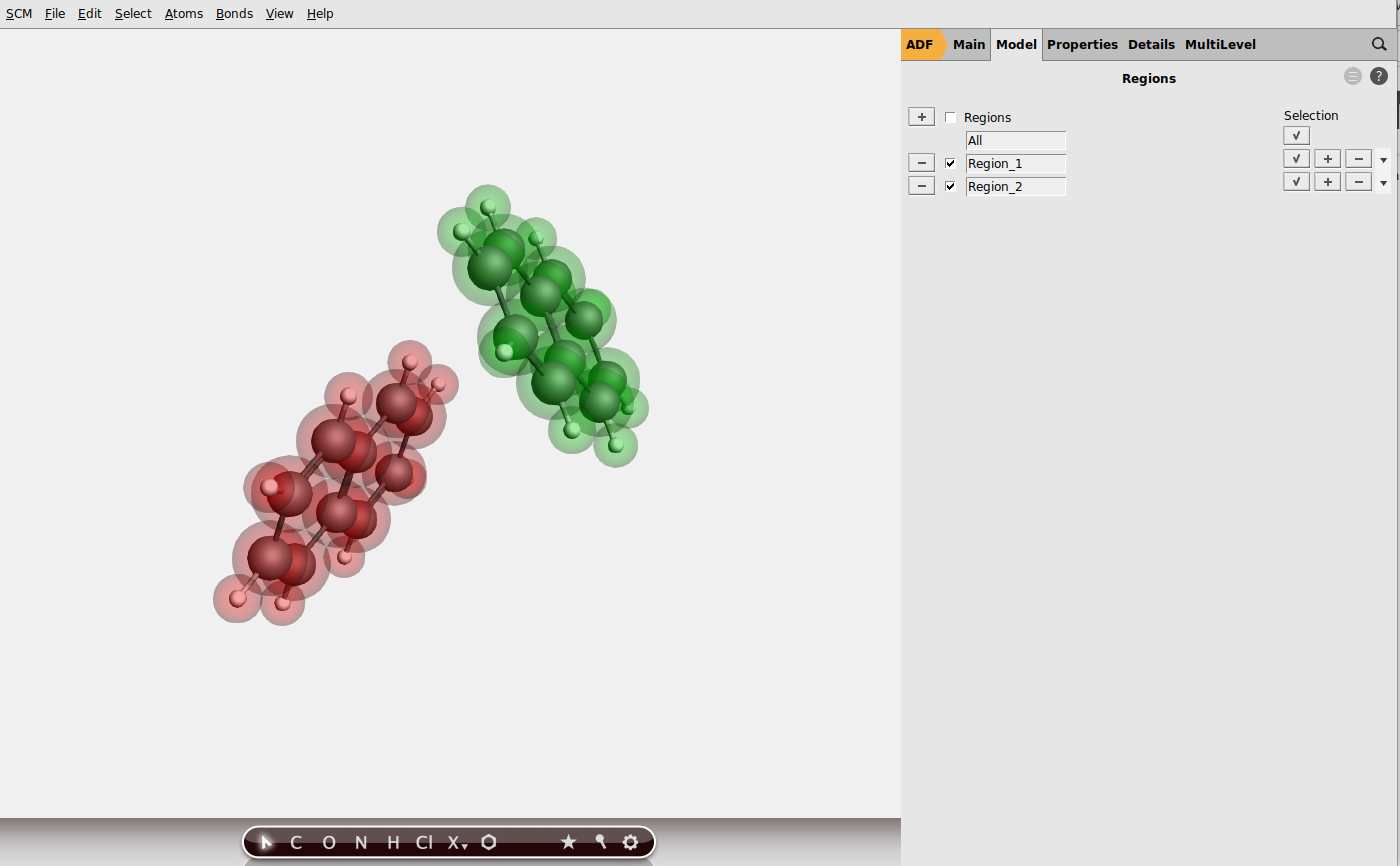
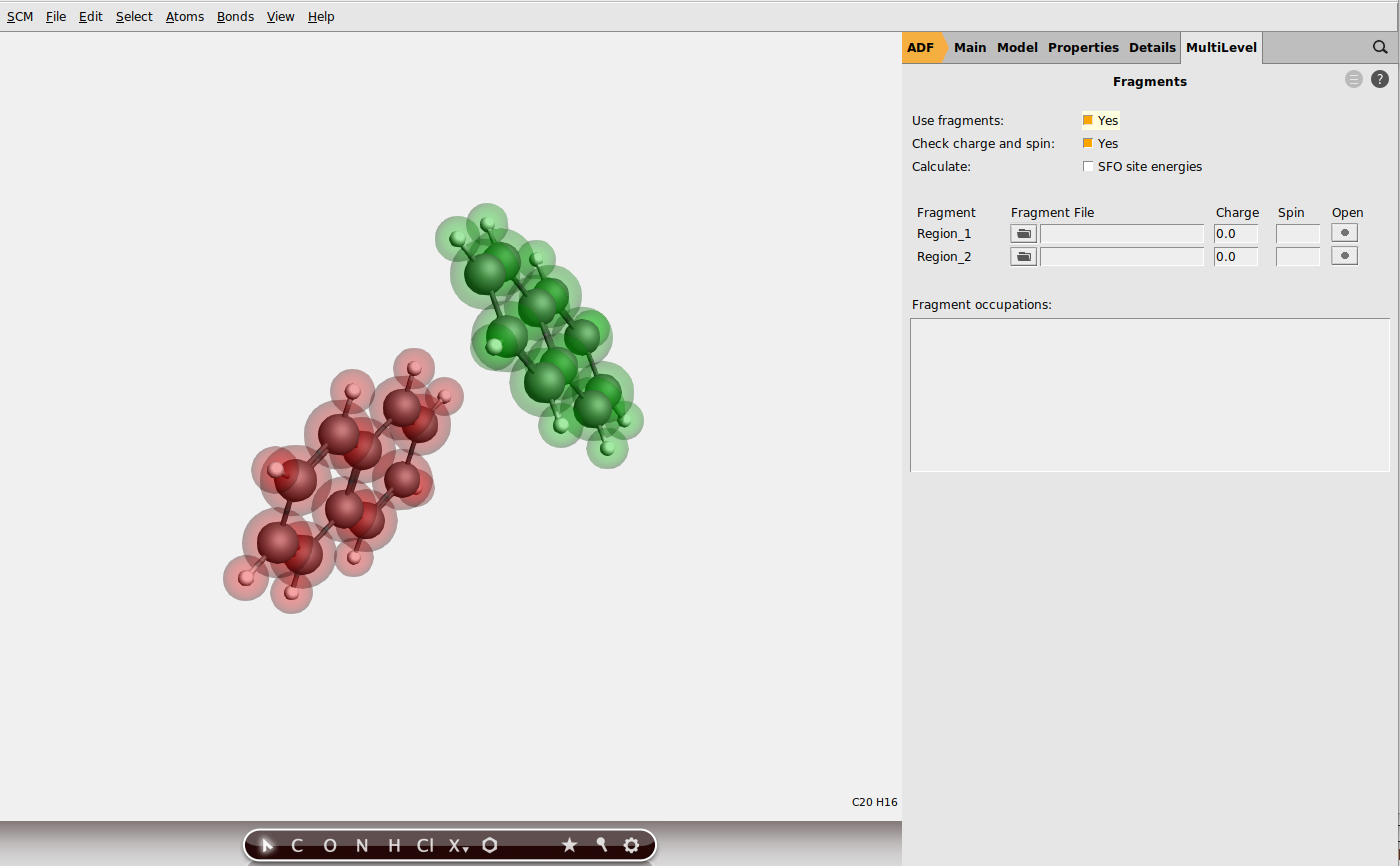
You can read more about ADF’s fragments approach in the ADF manual or in the ADF fragments tutorial.
Transport properties and settings¶
When using molecular fragments in ADF, multiple calculations will be (automatically) performed: first, each fragment is computed individually (in this case, the individual naphthalene molecules). Then the calculation of the full system is performed in which the Hamiltonian matrix elements are expressed in the basis of the molecular orbitals of the fragments. It is within this framework that the site energies, charge transfer integrals and overlap integrals between fragment orbitals are computed. More information on this can be found in the charge transfer integrals section of the ADF manual and in the following publications by Senthilkumar et al. [1] [2].
When the job is finished, we search for the charge transfer integrals in the output:
Generalized Charge Transfer Integrals¶
The electronic coupling V (also known as effective or generalized charge transfer integral Jeff) that goes into Marcus theory is calculated as (see e.g. Wen et al. [3] )
J is the transfer integral, S the overlap, and ε the site energy.
The generalized charge transfer integrals and the components are printed in the output:
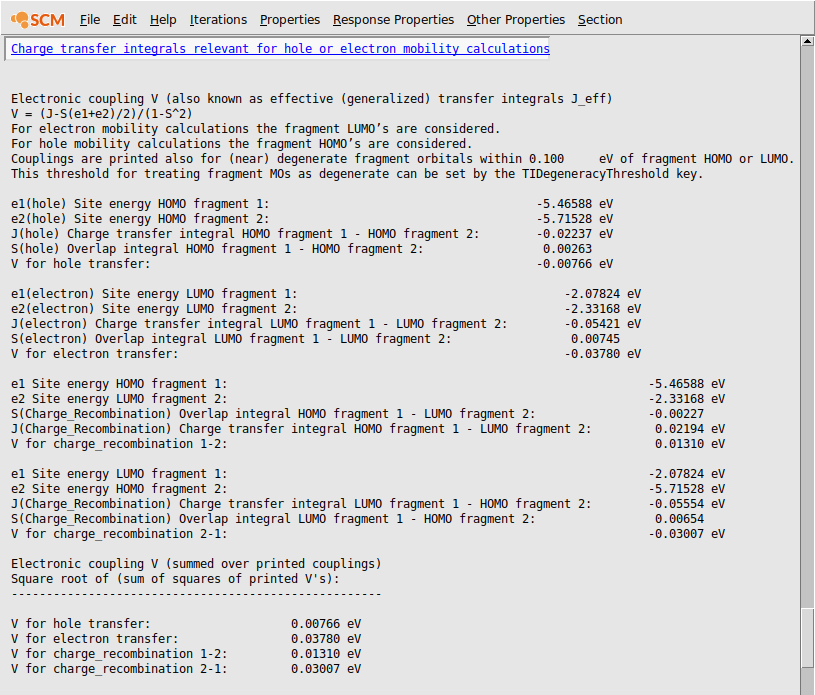
The electronic coupling between these two naphthalene molecules is thus calculated as 0.00766 eV for hole transport and 0.03780 eV for electron transport.
Look at the tab results in Coropceanu et al. [4] for more information. The signs of J and S depend on the phase of orbitals (which is arbitrary). Since V2 is used in the Marcus equation, the sign does not affect the hopping rates.
Reorganization energies¶
The reorganization energy λ is defined as the energy difference between the charged and neutral systems at the two different geometries (adiabatic PES). E.g. for electron transfer:
We therefore need to perform four calculations: two geometry optimizations and two single point calculations.
First, set up the geometry optimization for the neutral naphthalene (from which we will obtain \(E^\text{neutral}_\text{neutral geometry}\)):
naphthalene_dimer.xyz
Then, set up the geometry optimization for the anion (from which we will obtain \(E^\text{anion}_\text{anion geometry}\)):
-11Run the two geometry optimizations:
We now need to run the two single point calculations:
Collect the four bonding energies from either the output files or the log files (see tutorial on 10 Ways to Get the Energy and Other Properties).
\(E^\text{anion}_\text{anion geometry} = -119.3514 \text{[eV]}\)
\(E^\text{anion}_\text{neutral geometry} = -119.2451 \text{[eV]}\)
\(E^\text{neutral}_\text{neutral geometry} = -119.4217 \text{[eV]}\)
\(E^\text{neutral}_\text{anion geometry} = -119.3142 \text{[eV]}\)
and calculate λ which is around 0.21 eV at this level of theory.
Hopping rates from Marcus theory¶
The Marcus rate for charge hopping between two sites is:
In our example (V = 6.06 10-21 J, λ = 3.36 10-20 J) the Marcus hopping rate for electrons is 6.9 1012 s-1 at 300K.
Macroscopic charge mobilities can be obtained from these hopping rates via Monte Carlo (e.g. Kwiatkowski et al. [5] ) or analytical approaches to calculate the diffusion coefficient that goes into the Einstein relation (e.g. Wen et al. [3] ).
Further considerations for charge mobilities¶
As shown by Sutton et al. [6] , the transfer integrals depend strongly on the amount of exact exchange. The GGA functional PW91 has often been used with good results. Likewise, the site energies and reorganization energies will also depend on the functional used. For λ often hybrids are used in the literature. Other technical settings may affect the accuracy of the calculation as well: basis sets, numerical quality…
Pavanello et al. [7] have implemented electronic couplings with the frozen-density embedding framework in ADF. This approach also allows the inclusion of multiple molecules which will affect the electronic couplings. It is formally linear-scaling with the number of subsystems, hence enabling the study of environment effects on electronic transport in amorphous crystals. You can watch Pavanello’s web presentation on electronic couplings with FDE.
When many charge transfer integrals are needed (e.g. an amorphous crystal with many different dimer orientations), the calculation may be speeded up. Energy decomposition may be switched off, the SCF cycles can be set to 0 (with typically a small effect on the integrals), and the preparation and analysis can be streamlined by using PLAMS or the AMSprep and AMSreport tools.
Alternatively, one can do very fast, but more approximate, charge transfer integrals calculations with DFTB.
Charge transfer integrals with DFTB¶
More approximate charge transfer integrals can be calculated in a very fast way with DFTB, see the DFTB manual on charge transfer integrals. Note that the DFTB parametrizations typically give too low charge transfer integrals if they are compared with ADF results. Thus one may need to scale them, or use specifically optimized DFTB parameters (not available in AMS).
 →
→ 