K-Space¶
The K-Space sampling (i.e., the k-points used to sample the Brillouin Zone) is an important technical aspect of Band, as it influences heavily the accuracy, the CPU time and the memory usage of the calculation (see section Recommendations for k-space).
KSpace input block¶
The K-Space can be controlled via the KSpace input block. Two different k-space integration methods are available: the Regular Grid (default) and the Symmetric Grid.
KSpace
Type [Regular | Symmetric]
Quality [Auto | GammaOnly | Basic | Normal | Good | VeryGood | Excellent]
End
KSpace- Type:
Block
- Description:
Options for the k-space integration (i.e. the grid used to sample the Brillouin zone)
Type- Type:
Multiple Choice
- Default value:
Regular
- Options:
[Regular, Symmetric]
- GUI name:
K-space grid type
- Description:
The type of k-space integration grid used to sample the Brillouin zone (BZ) used. ‘Regular’: simple regular grid. ‘Symmetric’: symmetric grid for the irreducible wedge of the first BZ (useful when high-symmetry points in the BZ are needed to capture the correct physics of the system, graphene being a notable example).
Quality- Type:
Multiple Choice
- Default value:
Auto
- Options:
[Auto, GammaOnly, Basic, Normal, Good, VeryGood, Excellent]
- GUI name:
K-space
- Description:
Select the quality of the K-space grid used to sample the Brillouin Zone. If ‘Auto’, the quality defined in the ‘NumericalQuality’ will be used. If ‘GammaOnly’, only one point (the gamma point) will be used. The actual number of K points generated depends on this option and on the size of the unit cell. The larger the real space cell, the fewer K points will be generated. The CPU-time and accuracy strongly depend on this option.
Regular K-Space grid¶
By default, Band will look at the size of a lattice vectors and the KSpace quality to determine the number of k-points. The larger the lattice vector in real space, the smaller the reciprocal space vectors are, and as a result fewer k-points are needed. The following intervals will be distinguished: 0-5 Bohr, 5-10 Bohr, 10-20 Bohr, 20-50 Bohr, and beyond. Here is the table explaining how many k-points will be used along a lattice vector.
Lattice vector length |
Basic |
Normal |
Good |
VeryGood |
Excellent |
0-5 Bohr |
5 |
9 |
13 |
17 |
21 |
5-10 Bohr |
3 |
5 |
9 |
13 |
17 |
10-20 Bohr |
1 |
3 |
5 |
9 |
13 |
20-50 Bohr |
1 |
1 |
3 |
5 |
9 |
50- Bohr… |
1 |
1 |
1 |
3 |
5 |
By preferring odd-numbered values we can use a quadratic interpolation method, and have the \(\Gamma\) point in the grid. It is then reasonable to assume a decaying error when going to a better quality setting.
It is also possible to manually specify the number of k-space points along each reciprocal lattice vector
KSpace
Regular
NumberOfPoints integer_list
End
End
KSpace- Type:
Block
- Description:
Options for the k-space integration (i.e. the grid used to sample the Brillouin zone)
Regular- Type:
Block
- Description:
Options for the regular k-space integration grid.
NumberOfPoints- Type:
Integer List
- Description:
Use a regular grid with the specified number of k-points along each reciprocal lattice vector. For 1D periodic systems you should specify only one number, for 2D systems two numbers, and for 3D systems three numbers.
Symmetric K-Space grid (tetrahedron method)¶
The tetrahedron method can be useful when high symmetry points in the BZ are needed to capture the correct physics of the system, graphene being a notable example.
The number of k-points in the symmetric grid depends on the KSpace quality and on the length of the shortest lattice vector.
It is also possible to manually specify the symmetric k-space integration parameter:
KSpace
Symmetric
KInteg integer
End
End
KSpace- Type:
Block
- Description:
Options for the k-space integration (i.e. the grid used to sample the Brillouin zone)
Symmetric- Type:
Block
- Description:
Options for the symmetric k-space integration grid.
KInteg- Type:
Integer
- GUI name:
Accuracy
- Description:
Specify the accuracy for the Symmetric method. 1: absolutely minimal (only the G-point is used) 2: linear tetrahedron method, coarsest spacing 3: quadratic tetrahedron method, coarsest spacing 4,6,… (even): linear tetrahedron method 5,7…. (odd): quadratic method The tetrahedron method is usually by far inferior.
General Remark: The tetrahedron method samples the irreducible wedge of the first BZ, whereas the regular grid samples the whole, first BZ. As a rule of thumb you need to choose roughly twice the value for the regular grid. For example kspace 2 compares to grid 4 4 4, kspace 3 to grid 5 5 5, etc.. Sticking to this rule the number of unique k-points will be roughly similar.
Recommendations for k-space¶
Which K-Space quality to use depends very much a) the system you are studying and b) the property you are interested in. We strongly recommend you to test the effect of different K-Space qualities on your system and properties of interest.
As an example, in the following table we list the errors on formation energy and band gap for diamond using regular k-space grids of different qualities (using Excellent kSpace quality as reference).
KSpace quality |
Energy error / atom [eV] |
CPU time ratio |
|---|---|---|
Gamma-Only |
3.3 |
1 |
Basic |
0.6 |
2 |
Normal |
0.03 |
6 |
Good |
0.002 |
16 |
VeryGood |
0.0001 |
35 |
Excellent |
reference |
64 |
It is worthwhile noting that the errors due to finite k-space sampling in formation energies are to some extend systematic, and they partially cancel each other out when taking energy differences.
In general, metals (or narrow-gap semiconductor) require higher K-Space sampling than insulators. For insulators and wide-gap semiconductors, Normal K-Space quality often suffices. For Narrow-gap semiconductor and metals, Good K-Space quality is highly recommended. For geometry optimizations under pressure, Good K-Space quality is recommended.
Furthermore for certain properties, such as band gaps, Normal K-Space quality might not be enough to obtain reliable results. For example, in following figure we see how Normal K-Space quality is often not enough for computing band gaps (especially for the narrow-gap semiconductor of the top panel). For band gap prediction, it is recommended to use Good K-Space quality.
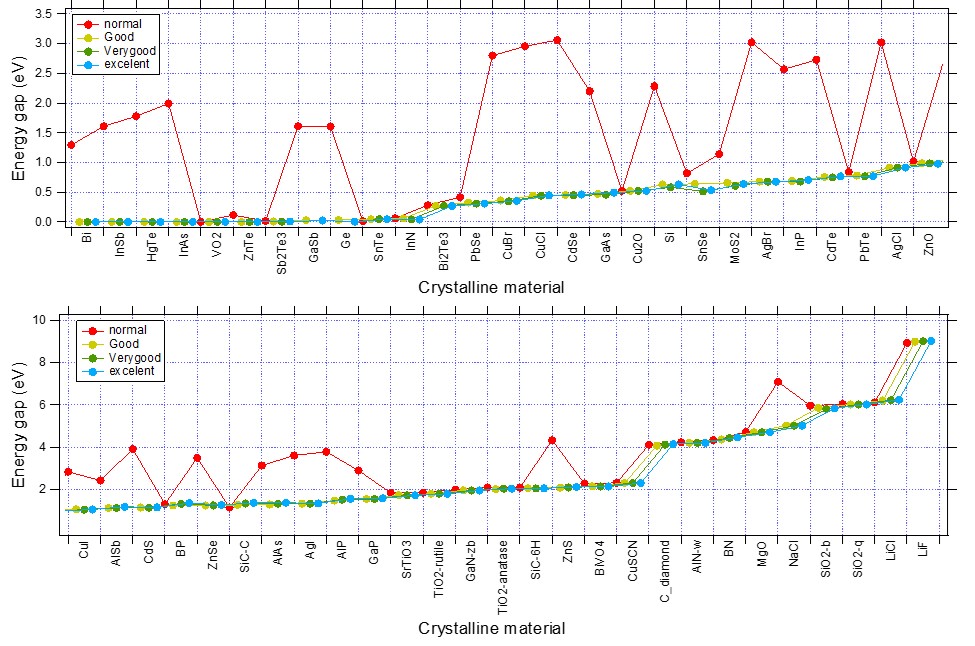
Fig. 4 Convergence of band gaps WRT the k-space quality set for various system. (XC:PBE, Basis:TZP)¶
High symmetry points and the regular grid¶
Using the symmetric k-grid it is ensured that points with high symmetry are included. However, for the default regular grid this is not the case. An important example is graphene. Its band structure has a conical intersection at the point labeled “K”, in all other k-points there is a gap.
grid |
point “K” included? |
K-grid quality for Graphene |
|---|---|---|
5x5 |
No |
Normal |
7x7 |
Yes |
|
9x9 |
No |
Good |
11x11 |
No |
|
13x13 |
Yes |
VeryGood |
15x15 |
No |
But in general it makes more sense to use the symmetric k-grid if points of high symmetry are deemed important.