Basis set¶
Band represents the single-determinant electronic wave functions as a linear combinations of atom-centered basis functions (the basis set). See also: Wikipedia page on Basis Sets.
The basis sets in Band consists of NAOs (Numerical Atomic Orbitals, obtained by solving numerically the Kohn-Sham equations for the isolated spherical atoms) augmented by a set of STOs (Slater Type Orbitals).
The choice of basis set is very important, as it influences heavily the accuracy, the CPU time and the memory usage of the calculation. Band comes with 6 predefined types of basis sets: SZ, DZ, DZP, TZP, TZ2P, QZ4P (SZ: Single Zeta, DZ: Double Zeta, DZP: Double Zeta + Polarization, TZP: Triple Zeta + Polarization, TZ2P: Triple Zeta + Double Polarization, QZ4P: Quadruple Zeta + Quadruple Polarization). See the sections Which basis set should I use? and Available Basis Sets for more details.
To speed up the calculation, Band can use the frozen core approximation in which core orbitals are kept frozen during the SCF procedure (and the valence orbitals are orthogonalized against the frozen orbitals). One can run an all electron calculation by specifying Core None in the Basis input block.
Note: some features, such as Hybrid functionals, are incompatible with the frozen-core approximation, and require an all electron (i.e. Core None) basis set.
Basis input block¶
You can specify which basis set to use in the Basis input block.
Basis
Type [SZ | DZ | DZP | TZP | TZ2P | QZ4P | STO/TZ2P | STO/SZ | STO/DZ | STO/DZP | STO/QZ4P |
CORR/QZ6P | CORR/TZ3P | GTO/CC-PV5Z | GTO/DEF2-QZVPPD | GTO/CC-PV6Z | GTO/CC-PVQZ |
GTO/CC-PVTZ | GTO/CC-PVDZ | GTO/DEF2-SVP | GTO/DEF2-TZVP | GTO/DEF2-TZVPP | GTO/DEF2-QZVP |
GTO/AUG-CC-PVDZ | GTO/AUG-CC-PVTZ | GTO/AUG-CC-PVQZ | GTO/POB-TZVP]
Core [None | Small | Medium | Large]
End
Basis- Type:
Block
- Description:
Definition of the basis set
Type- Type:
Multiple Choice
- Default value:
DZ
- Options:
[SZ, DZ, DZP, TZP, TZ2P, QZ4P, STO/TZ2P, STO/SZ, STO/DZ, STO/DZP, STO/QZ4P, CORR/QZ6P, CORR/TZ3P, GTO/CC-PV5Z, GTO/DEF2-QZVPPD, GTO/CC-PV6Z, GTO/CC-PVQZ, GTO/CC-PVTZ, GTO/CC-PVDZ, GTO/DEF2-SVP, GTO/DEF2-TZVP, GTO/DEF2-TZVPP, GTO/DEF2-QZVP, GTO/AUG-CC-PVDZ, GTO/AUG-CC-PVTZ, GTO/AUG-CC-PVQZ, GTO/POB-TZVP]
- GUI name:
Basis set
- Description:
Select the basis set to use. SZ : Single Z DZ : Double Z DZP : Double Z, 1 polarization function TZP : Triple Z, 1 polarization function TZ2P : Triple Z, 2 polarization functions QZ4P : Quadruple Z, 4 polarization function The basis set chosen will apply to all atoms in your structure. If a matching basis is not found a better type might be used.
Core- Type:
Multiple Choice
- Default value:
Large
- Options:
[None, Small, Medium, Large]
- GUI name:
Frozen core
- Description:
Select the size of the frozen core you want to use. Small, Medium, and Large will be interpreted within the basis sets available (of the selected quality), and might refer to the same core in some cases.
Which basis set should I use?¶
The hierarchy of basis sets, from the smallest and least accurate (SZ) to the largest and most accurate (QZ4P), is SZ < DZ < DZP < TZP < TZ2P < QZ4P.
The choice of basis set is in general a trade off between accuracy and computation time: the more accurate the basis set, the more computationally demanding the calculation will be (both in term of CPU time and the memory usage).
As an example, in the following table we compare accuracy v.s. CPU time for a (24,24) carbon nanotube using different basis sets. “Energy error” is defined as the absolute error in the formation energy per atom using the QZ4P results as reference. [1]
Basis Set |
Energy Error [eV] |
CPU time ratio (relative to SZ) |
|---|---|---|
SZ |
1.8 |
1 |
DZ |
0.46 |
1.5 |
DZP |
0.16 |
2.5 |
TZP |
0.048 |
3.8 |
TZ2P |
0.016 |
6.1 |
QZ4P |
reference |
14.3 |
It is worthwhile noting that the error in formation energies are to some extend systematic, and they partially cancel each other out when taking energy differences. For example, if one considers the difference in energy between two carbon nanotubes variants ((24,24) and (24-0)) with the same number of atoms, the basis set error is smaller than 1 milli-eV/atom already with a DZP basis set, which is much smaller than the absolute error in the individual energies. The same consideration holds for reactions barriers: the error in the energy difference between different conformations is much smaller than the error in the absolute energies themselves.
Band gaps:
The following figure shows the convergence WRT basis set of band gaps (XC:PBE). While DZ is often inaccurate (since DZ lacks any polarization function, the description of the virtual orbital space is very poor), TZP captures the trends very well.
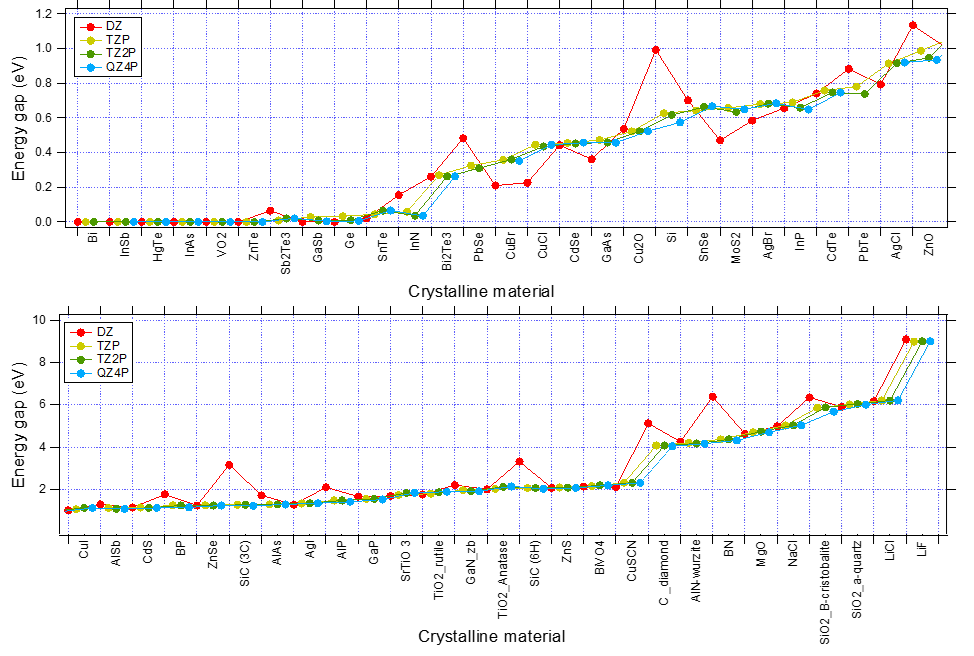
Fig. 3 Convergence of Band Gaps WRT basis set for various system. (XC:PBE, K-Space Quality: Good)¶
In general, since the basis set might have different effects on different properties, it is advisable to run a few simple calculations to get an idea of the effect of the basis set with your property of interest.
A summary of the basis sets:
SZ: Single Zeta, the minimal basis set (only NAOs), serves mostly a technical purpose. The results are rather inaccurate, but it’s computationally efficient. It can be useful for running a very quick test calculation. See also SZ-SCF-Restart.
DZ: The Double Zeta basis set is computationally very efficient. It can be used for pre-optimization of structures (that should then be further optimized with a better basis set). Since it has no polarization functions, properties depending on the virtual orbital space will be rather inaccurate.
DZP: Double zeta plus polarization function. Only available for main group elements up to Krypton. For other elements a TZP basis set will be used automatically. This is a reasonably good basis set for geometry optimizations of organic systems.
TZP: The Triple Zeta plus Polarization basis set offers the best balance between performance and accuracy. This is the basis set we would generally recommend.
TZ2P: The Triple Zeta plus Double Polarization basis set is an accurate basis set. It is qualitatively similar to TZP but quantitatively better. It should be used when a good description of the virtual orbital space is needed.
QZ4P: Quadruple zeta plus Quadruple Polarization. This is the biggest basis set available. It can be used for benchmarking.
Frozen core¶
It is recommended to use the frozen core approximation, as it is faster, in particular for heavy elements.
In general, the frozen core approximation does not influence the results significantly (especially if one uses a small frozen core). For accurate results on certain properties (like Properties at Nuclei) all electron basis sets are needed on the atoms of interest.
For Meta-GGA XC functionals, it is recommended to use
smallornonefrozen core (the frozen orbitals are computed using LDA and not the selected Meta-GGA)For optimizations under pressure, use
smallornonefrozen core
Small, Medium, and Large frozen cores:
The possible choices for the Basis%Core keyword are None, Small, Medium, and Large. How does this map to the actual Available Basis Sets? Obviously this depends on the element. As all elements have an all electron basis set defined, None maps always to this set.
For the element H there are no frozen core sets available and all options can only lead to the all electron basis set. For elements like C there is a single frozen core available and the three choices (Small, Medium, Large) lead to the same choice: C.1s. Most elements have two frozen cores defined. In such a case the choices Large and Medium point to the larger one, and Small to the smallest one. With four choices Large maps to the largest one, Medium to the one below it, and Small to the smallest one. This table summarizes the logic
#Available frozen cores |
Example |
None |
Small |
Medium |
Large |
|---|---|---|---|---|---|
0 |
H |
H |
H |
H |
H |
1 |
C C.1s |
C |
C.1s |
C.1s |
C.1s |
2 |
Na Na.1s Na.2p |
Na |
Na.1s |
Na.2p |
Na.2p |
3 |
Rb Rb.3p Rb.3d Rb.4p |
Rb |
Rb.3p |
Rb.3d |
Rb.4p |
4 |
Pb Pb.4d Pb.4f Pb.5p Pb.5d |
Pb |
Pb.4d |
Pb.5p |
Pb.5d |
It is possible to control both the basis and core per atom type and per region, see More Basis input options.
Available Basis Sets¶
The basis set files, containing the definition of the basis set, are located in $AMSHOME/atomicdata/Band.
The next table gives an indication frozen core (fc) standard basis sets are available for the different elements in BAND. Note that all electron (ae) basis set are available for all basis sets types.
Element |
frozen core |
SZ, DZ |
DZP |
TZP, TZ2P, QZ4P |
|---|---|---|---|---|
H-He (Z=1-2) |
ae |
Yes |
Yes |
Yes |
Li-Ne (Z=3-10) |
ae .1s |
Yes |
Yes |
Yes |
Na-Mg (Z=11-12) |
ae .1s .2p |
Yes |
Yes |
Yes |
Al-Ar (Z=13-18) |
ae .1s .2p |
Yes |
Yes |
Yes |
K-Ca (Z=19-20) |
ae .2p .3p |
Yes |
Yes |
Yes |
Sc-Zn (Z=21-30) |
ae .2p .3p |
Yes |
Yes |
|
Ga-Kr (Z=31-36) |
ae .3p .3d |
Yes |
Yes |
Yes |
Rb-Sr (Z=37-38) |
ae .3p .3d .4p |
Yes |
Yes |
|
Y-Cd (Z=39-48) |
ae .3d .4p |
Yes |
Yes |
|
In-Ba (Z=49-56) |
ae .4p .4d |
Yes |
Yes |
|
La-Lu (Z=57-71) |
ae .4d .5p |
Yes |
Yes |
|
Hf-Hg (Z=72-80) |
ae .4d .4f |
Yes |
Yes |
|
Tl (Z=81) |
ae .4d .4f .5p |
Yes |
Yes |
|
Pb-Rn (Z=82-86) |
ae .4d .4f .5p .5d |
Yes |
Yes |
|
Fr-Ra (Z=87-88) |
ae .5p .5d |
Yes |
Yes |
|
Ac-Lr (Z=89-103) |
ae .5d .6p |
Yes |
Yes |
|
Rf-Og (Z=104-118) |
ae .5d .5f |
Yes |
Yes |
|
Uue-Ubn (Z=119-120) |
ae .5f |
Yes |
Yes |
element name (without suffix): all electron (ae)
.1s frozen: 1s
.2p frozen: 1s 2s 2p
.3p frozen: 1s 2s 2p 3s 3p
.3d frozen: 1s 2s 2p 3s 3p 3d
.4p frozen: 1s 2s 2p 3s 3p 3d 4s 4p
.4d frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d
.4f frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f
.5p frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 5s 5p (La-Lu)
.5p frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p (other)
.5d frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d
.6p frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 6s 6p (Ac-Lr)
.5f frozen: 1s 2s 2p 3s 3p 3d 4s 4p 4d 4f 5s 5p 5d 5f 6s 6p
Note
Not all combinations of basis set Type and Core are available for all elements. If a specific combination is not available, Band will pick the first better basis set. E.g. if an element is not in the DZP database, it is taken from the TZP basis set.
Pure STO and GTO basis sets¶
Starting from AMS2023, BAND includes many basis sets to reproduce literature data. The basis sets are suitable (and recommended) for well converged GW, RPA, and double hybrid calculations in which electron-electron interaction effects are accounted for explicitly beyond DFT. Available basis sets are:
pure STO type basis sets
The TZ2P and QZ4P basis sets from ADF can now be used in BAND calculations as well. To get the same results as ADF, it is additionally necessary to disable the confinement of the basis functions Confinement of basis functions. Additionally, the CORR/TZ3P and the CORR/QZ6P basis sets of ADF can also be used with BAND. Band also includes the Corr/TZ3P_G and the Corr/QZ6P_GH basis sets which includes higher-angular momentum functions (g-functions fo TZ3P_G, g-,h- (and sometimes i-)functions for QZ6P_GH).
Basis Type=STO/TZ2PSTO
SoftConfinement Quality=Excellent # disable radial basis function confinement
Basis Set |
ADF |
|---|---|
STO/TZ2PSTO |
ZORA/TZ2P |
STO/QZ4PSTO |
ZORA/QZ4P |
CORR/QZ6P |
CORR/QZ6P |
CORR/QZ6P_GH |
|
CORR/TZ3P |
CORR/TZ3P |
CORR/TZ3P_G |
Correlation consistent Gaussian type basis sets
See also
BAND includes the correlation-consistent (CC) Dunning Gaussian type (GTO) basis sets from double Zeta (DZ) to hextuple Zeta (6Z) quality. GTO basis sets can only be used in non-relativistic calculations and can not be used with the frozen core approximation. The basis sets cc-pVDZ to cc-pV5Z are only available for the first four rows of the periodic table, with the exception of K (potassium) (see also: the information on the Basis Set Exchange. The cc-pV6Z basis set is only available for the elements of the first three rows of the periodic table with the exception of Li, Na, and Mg.
Basis Type=GTO/CC-PVTZ
SoftConfinement Quality=Excellent # disable radial basis function confinement
Relativity Level=None # relativistic effects are currently not supported for GTOs
Basis Set |
comment |
|---|---|
GTO/CC-PV5Z |
|
GTO/CC-PV6Z |
|
GTO/CC-PVDZ |
|
GTO/CC-PVQZ |
|
GTO/CC-PVTZ |
|
GTO/CC-PWCVQZ |
GTO type basis sets can be used to calculate high-quality RPA and MP2/double-hybrid energies as well as GW QP energies (MBPT based methods), often in combination with complete basis set (CBS) limit extrapolation of the form
where \(E_{Y}\) denotes an energy or QP energy calculated with the cc-pVYZ basis set and \(E_{X}\) denotes an energy or QP energy calculated with the cc-pVXZ basis set, and \(Y > X\) . Typically, an extrapolation from a cc-pVTZ and a cc-pVQZ calculation will give a result of cc-pV5Z quality at lower computational cost.
When used in conjunction with MBPT based methods, a highly accurate auxiliary fit set is needed (Also see the recommendations in the MBPT section). It is recommended to generate the auxiliary fit sets directly from products of basis functions to saturate all higher angular momentum channels. See the RIHartreeFock documentation.
More Basis input options¶
Basis
Folder string
PerAtomType
Core [None | Small | Medium | Large]
File string
Symbol string
Type [SZ | DZ | DZP | TZP | TZ2P | QZ4P]
End
PerRegion
Core [None | Small | Medium | Large]
Region string
Type [SZ | DZ | DZP | TZP | TZ2P | QZ4P]
End
End
Basis- Type:
Block
- Description:
Definition of the basis set
Folder- Type:
String
- Description:
Path to a folder containing the basis set files. This can be used for special use-defined basis sets. Cannot be used in combination with ‘Type’
PerAtomType- Type:
Block
- Recurring:
True
- Description:
Defines the basis set for all atoms of a particular type.
Core- Type:
Multiple Choice
- Options:
[None, Small, Medium, Large]
- Description:
Size of the frozen core.
File- Type:
String
- Description:
The path to the basis set file. The path can be absolute or relative to $AMSRESOURCES/Band. Specifying the path to the basis file explicitly overrides the automatic basis file selection via the Type and Core subkeys.
Symbol- Type:
String
- Description:
The symbol for which to define the basis set.
Type- Type:
Multiple Choice
- Options:
[SZ, DZ, DZP, TZP, TZ2P, QZ4P]
- Description:
The basis sets to be used.
PerRegion- Type:
Block
- Recurring:
True
- Description:
Defines the basis set for all atoms in a region. If specified, this overwrites the values set with the Basis%Type and Basis%PerAtomType keywords for atoms in that region. Note that if this keyword is used multiple times, the chosen regions may not overlap.
Core- Type:
Multiple Choice
- Default value:
Large
- Options:
[None, Small, Medium, Large]
- Description:
Size of the frozen core.
Region- Type:
String
- Description:
The identifier of the region for which to define the basis set. Note that this may also be a region expression, e.g. ‘myregion+myotherregion’ (the union of two regions).
Type- Type:
Multiple Choice
- Default value:
DZ
- Options:
[SZ, DZ, DZP, TZP, TZ2P, QZ4P]
- Description:
The basis sets to be used.
See also: Example: Multiresolution, and Frozen core.
Confinement of basis functions¶
It is possible to alter the radial part of the basis functions in order to make them more compact, which will in turn speeds up the calculation.
SoftConfinement
Quality [Auto | Basic | Normal | Good | VeryGood | Excellent]
Radius float
Delta float
End
SoftConfinement- Type:
Block
- Description:
In order to make the basis functions more compact, the radial part of the basis functions is multiplied by a Fermi-Dirac (FD) function (this ‘confinement’ is done for efficiency and numerical stability reasons). A FD function goes from one to zero, controlled by two parameters. It has a value 0.5 at Radius, and the decay width is Delta.
Quality- Type:
Multiple Choice
- Default value:
Auto
- Options:
[Auto, Basic, Normal, Good, VeryGood, Excellent]
- GUI name:
Confinement
- Description:
In order to make the basis functions more compact, the radial part of the basis functions is multiplied by a Fermi-Dirac (FD) function (this ‘confinement’ is done for efficiency and numerical stability reasons). A FD function goes from one to zero, controlled by two parameters. It has a value 0.5 at Radius, and the decay width is Delta. This key sets the two parameters ‘Radius’ and ‘Delta’. Basic: Radius=7.0, Delta=0.7; Normal: Radius=10.0, Delta=1.0; Good: Radius=20.0, Delta=2.0; VeryGood and Excellent: no confinement at all. If ‘Auto’, the quality defined in the ‘NumericalQuality’ will be used.
Radius- Type:
Float
- Unit:
Bohr
- Description:
Explicitly specify the radius parameter of the Fermi-Dirac function.
Delta- Type:
Float
- Unit:
Bohr
- Description:
Explicitly specify the delta parameter of the Fermi-Dirac function (if not specified, it will be 0.1*Radius).
For geometry optimizations under pressure,
Basicsoft confinement is recommended.
Manually specifying AtomTypes (expert option)¶
AtomType (block-type)(Expert Option) Description of the atom type. Contains the block keys
Dirac,BasisFunctionsandFitFunctions. The key corresponds to one atom type. The ordering of theAtomTypekeys (in case of more than one atom type) is NOT arbitrary. It is interpreted as corresponding to the ordering of theAtomskeys. The n-thAtomTypekey supplies information for the numerical atom of the nth type, which in turn has atoms at positions defined by the nthAtomskey.AtomType ElementSymbol Dirac ChemSym {option} ... shells cores shell_specification {occupation_number} ... End {BasisFunctions shell_specification STO_exponent ... End} FitFunctions shell_specification STO_exponent ... End END
The argument ElementSymbol to
AtomTypeis the symbol of the element that is referred to in theAtomskey block.Dirac (block-type)Specification of the numerical (‘Herman-Skillman’) free atom, which defines the initial guess for the SCF density, and which also (optionally) supplies Numerical Atomic Orbitals (NOs) as basis functions, and/or as STO fit functions for the crystal calculation. The argument ChemSym of this option is the symbol of the element of the atom type. The data records of the
Dirackey are:the number of atomic shells (1s,2s,2p,etc.) and the nr. of core-shells (two integers on one line).
specification of the shell and its electronic occupation.
This specification can be done via quantum numbers or using the standard designation (e.g. ‘1 0’ is equivalent to ‘1s’). Optionally one may insert anywhere in the Dirac block a record Valence, which signifies that all numerical valence orbitals will be used as basis functions (NOs) in the crystal calculation. You can also insert NumericalFit followed by a number (max. \(l\)-value) in the key block, which causes the program to use numerical STO fit functions. For example NumericalFit 2 means that the squares of all s,p, and d NOs will be used as STO fit functions with \(l=0\), since the NOs are spherically symmetric. If you insert Spinor, a spin-orbit relativistic calculation for the single-atom will be carried out.
The Herman-Skillman program generates all its functions (atomic potential, charge density, one-electron states) as tables of values in a logarithmic radial grid. The number of points in the grid, and the min. and max. r-value are defaulted at 3000, 0.000001, and 100.0 (a.u.) respectively. These defaults can be overwritten by specifying anywhere in the Dirac block the (sub)keys radial, rmin and rmax.
The program will do a spin-unrestricted calculation for the atoms in addition to the restricted one. The occupation of the spin-orbitals will be of maximum spin-multiplicity and cannot be controlled in the Dirac key-block.
BasisFunctions (block-type)Slater-type orbitals, specified by quantum numbers \(n\),:math:l or by the letter designation (e.g. 2p) and one real (alpha) per STO. One STO per record. Use of this key is optional in the sense that Slater-type functions are not needed if other basis functions have been specified (i.e. the numerical atomic orbitals, see key Dirac).
FitFunctions (block-type)Slater-type fit functions, described in the same way as in
BasisFunctions. EachFitFunctionskey corresponds to one atom type, the type being the one of the precedingDirackey. The selection choice of a ‘good’ fit set is a matter of experience. Fair quality sets are included in the database of the molecular program ADF.Example:
AtomType C :: Carbon atom Dirac C 3 1 VALENCE 1s 2s 2p 2.0 End BasisFunctions 1s 1.7 ... End FitFunctions 1s 13.5 2s 11.0 ... End End
TestFunctions (block-type)An optional subkey of the
AtomTypekey block isTestFunctionswhich has the same format as theBasisFunctionsandFitFunctionsblocks. TheTestFunctionsblock specifies STOs to be used as test functions in the numerical integration package. For the time being the \(l\) value is ignored. A possible application is to include a very tight function, to increase the accuracy near a nucleus.
Basis Set Superposition Error (BSSE)¶
The Ghost Atom feature enables the calculation of Basis Set Superposition Errors (BSSE). Normally, if you want to know the bonding energy of system A with system B you calculate three energies
\(E(A+B)\)
\(E(A)\)
\(E(B)\)
The bond energy is then \(E(A+B) - E(A) - E(B)\)
The BSSE correction is about the idea that we can also calculate E(A) including basis functions from molecule B.
You can make a ghost atom by simply adding “Gh.” in front of the element name, for instance “Gh.H” for a ghost hydrogen , “Gh.C” for a ghost Carbon atom.
You will get a better bonding energy, closer to the basis set limit by calculating
\(E(A+B) - E(\text{A with B as ghost}) - E(\text{B with A as ghost})\)
The BSSE correction is
\(E(A) - E(\text{A with B as ghost}) + E(B) - E(\text{B with A as ghost})\)
See also
Footnotes
Alternative elements / Virtual crystal approximation¶
It is possible to define an alternative nuclear charge for an element. If a certain site in a crystal has, say, a 50% occupation of C (Z=6) and a 50% occupation of B (Z=5) you can use one alternative atom with Z=5.5
Example:
Atoms
Si 0.0 0.0 0.0
C 0.0 0.0 0.0 nuclear_charge=5.5 ! this site has a mixture of 50% C and B
End
In this example the basis set is taken from the C atom, but you could equally well specify the B atom here. (In fact any atom type can be specified here, but why would you like to use an Au basis set for this situation.). Defining such an average element is in the spirit of the Virtual Crystal Approximation (VCA), however, the fractional nuclear charge approach does not work well when for instance the fractional z is near the value of a noble gas. For instance when mixing Si (Z=14) and C(Z=8) atoms you may get near Ne (Z=10), and the corresponding lattice will be way too diffuse.
If you want to perform a scan it can be useful to use the ModifyAlternativeElement option
Example:
System
ModifyAlternativeElements true
Atoms
Si 0.0 0.0 0.0
H 0.0 0.0 0.0 nuclear_charge=5.6 ! Element H is ignored and will be "rounded" to nearest atom (for the basis set) in this case C
End
In band an alternative element works well with the frozen core approximation, using a smaller or no core has little effect. The VCA relies on defining an average pseudopotential (commonly used in plane wave programs) and is not identical to the alternative element approach (defining an average nuclear charge).