Optical Properties: Time-Dependent Current DFT¶

Time-Dependent Current Density Functional Theory (TD-CDFT) is a theoretical framework for computing optical response properties, such as the frequency-dependent dielectric function.

In this section, the TD-CDFT implementation for extended systems (1D, 2D and 3D) in BAND is described. The input keys are described in NewResponse or in OldResponse.

Some examples are available in the $AMSHOME/examples/band directory and are discussed in the Examples section.

Insulators, semiconductors and metals¶

The TD-CDFT module enables the calculation of real and imaginary parts of the material property tensor $\chi_e(\omega)$, called the electric susceptibility. The electric susceptibility is related to the macroscopic dielectric function, $\varepsilon_M(\omega)$.

For semi-conductors and insulator, for which the bands are either fully occupied or fully unoccupied, the dielectric function $\varepsilon_M(\omega)$ comprises only of the so called interband component:

\[\varepsilon_M(\omega) = 1 + 4 \pi \chi_e(\omega)\]

In general $\chi_e(\omega)$ and $\varepsilon_M(\omega)$ are tensors. They, however, simplify to scalars in isotropic systems.

For metals, for which partially-occupied bands exist, there is a so called intraband component arising due to transitions within a partially-occupied band:

\[\varepsilon_M(\omega) = 1 + 4 \pi \chi_e(\omega) - 4 \pi i \sigma_e(\omega) / \omega\]

Frequency dependent kernel¶

It is known that the exact Vignale-Kohn (VK) kernel greatly improves the static polarizabilities of infinite polymers and nanotubes (see reference), but gives bad results for the optical spectra of semiconductors and metals. For the low frequency part one needs a frequency dependent kernel, since Drude-like tails are completely absent in the adiabatic local density approximation (ALDA). With a modified VK kernel, which neglects $\mu_{xc}$ so that it reduces to the ALDA form in the static limit (see reference), much better results can be obtained. BAND currently only supports the modified VK kernel in either the QV or CNT parametrization, and it should only be used for metals.

EELS¶

From the macroscopic dielectric function it is possible to calculate the electron energy loss function (EELS). In transmission EELS one studies the inelastic scattering of a beam of high energy electrons by a target. The scattering rates obtained in these experiments are related to the dynamical structure factor $S(q,\omega)$ [A1]. In the special case with wavevector $q=0$, $S(q,\omega)$ is related to the longitudinal macroscopic dielectric function. This is the long-wave limit of EELS. For isotropic system the dielectric function is simply a scalar ($1/3 \text{Tr} (\varepsilon_M(\omega))$ ). In this case the long-wave limit of the electron energy loss function assumes the trivial form

\[\lim_{q \rightarrow 0} 2 \pi \frac{S(q,\omega)}{q^2 V} = \frac{\varepsilon_2}{\varepsilon_1^2 + \varepsilon_2^2}\]

with $\varepsilon_1$ and $\varepsilon_2$ as real and imaginary part of the dielectric function.

References

The three related Ph.D. theses, due to F. Kootstra (on TD-DFT for insulators), P. Romaniello (on TD-CDFT for metals), and A. Berger (on the Vignale-Kohn functional in extended systems) contain much background information, and can be downloaded from the SCM website.

The most relevant publications on this topic due to the former “Groningen” group of P.L. de Boeij are 1 2 3 4.

[A1] S. E. Schnatterly, in Solid State Physics Vol.34, edited by H. Ehrenreich, F. Seitz, and D. Turnbull (Academic Press, Inc., New York, 1979).

Input Options¶

In the 2017 release of BAND there are two implementations of the TD-CDFT formalism. The original implementation, relying on obsolete algorithms of BAND, is accessible via the OldResponse key block. The new code section, relying on more modern algorithms of BAND, is accessible via the NewResponse, NewResponseSCF and NewResponseKSpace key blocks. The differences between the two flavors are summarized in the following table:

	OldResponse	NewResponse
3D-systems	yes	yes
2D-systems	no	yes
1D-systems	(yes)	yes
Semiconductors	yes	yes
Metals	yes	(yes)
ALDA	yes	yes
Vignale-Kohn	yes	no
Berger2015 (3D)	yes	yes
Scalar ZORA	yes	yes
Spin Orbit ZORA	yes	no

Besides these differences, one should not expect both flavors to give the exact same result, if the reciprocal space limit is not reached! This can be explained by different approaches to evaluate the integration weights of single-particle transitions in reciprocal space.

Attention

Response properties converge slowly with respect to k-space sampling (number of k-points). Always check the convergence of $\varepsilon_M$ with respect to K-Space options!!!

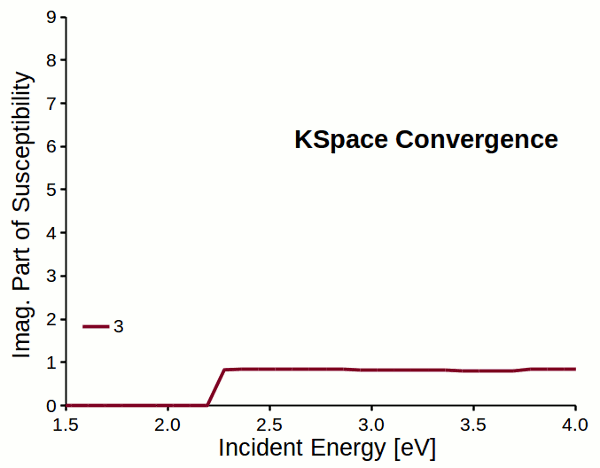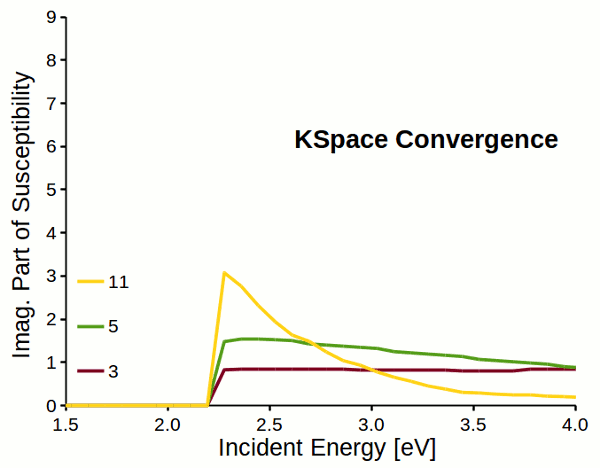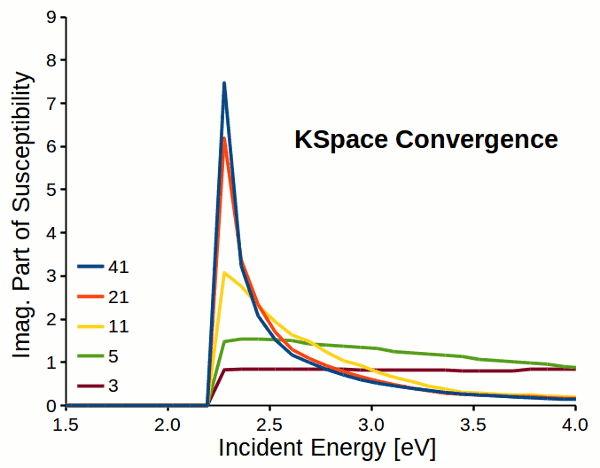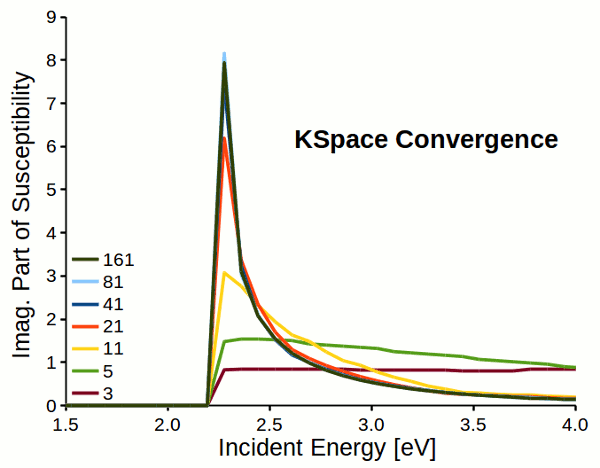
../_images/Conv_H2.gif — Fig. 5 Reciprocal space sampling convergence of imaginary part of susceptibility for a dihydrogen chain.¶

NewResponse¶

The dielectric function is computed when the key block NewResponse is present in the input. Several important settings can be defined in this key block.

Additional details can be specified via the NewResponseKSpace and NewResponseSCF blocks.

NewResponse
   NFreq integer
   FreqLow float
   FreqHigh float
   EShift float
   ActiveESpace float
   DensityCutOff float
   ActiveXYZ string
End

NewResponse

Type: Block
Description: The TD-CDFT calculation to obtain the dielectric function is computed when this block is present in the input. Several important settings can be defined here.

NFreq

Type: Integer
Default value: 5
Description: Number of frequencies for which a linear response TD-CDFT calculation is performed.

FreqLow

Type: Float
Default value: 1.0
Unit: eV
Description: Lower limit of the frequency range for which response properties are calculated. (omega_{low})

FreqHigh

Type: Float
Default value: 3.0
Unit: eV
Description: Upper limit of the frequency range for which response properties are calculated (omega_{high}).

EShift

Type: Float
Default value: 0.0
Unit: eV
GUI name: Shift
Description: Energy shift of the virtual crystal orbitals.

ActiveESpace

Type: Float
Default value: 5.0
Unit: eV
GUI name: Active energy space
Description: Modifies the energy threshold (DeltaE^{max}_{thresh} = omega_{high} + ActiveESpace) for which single orbital transitions (DeltaEpsilon_{ia} = Epsilon_{a}^{virtual} - Epsilon_{i}^{occupied}) are taken into account.

DensityCutOff

Type: Float
Default value: 0.001
GUI name: Volume cutoff
Description: For 1D and 2D systems the unit cell volume is undefined. Here, the volume is calculated as the volume bordered by the isosurface for the value DensityCutoff of the total density.

ActiveXYZ

Type: String
Default value: t
Description: Expects a string consisting of three letters of either ‘T’ (for true) or ‘F’ (for false) where the first is for the X-, the second for the Y- and the third for the Z-component of the response properties. If true, then the response properties for this component will be evaluated.

NewResponseSCF
   Bootstrap integer
   COApproach Yes/No
   COApproachBoost Yes/No
   Criterion float
   DIIS
      Enabled Yes/No
      MaxSamples integer
      MaximumCoefficient float
      MinSamples integer
      MixingFactor float
   End
   LowFreqAlgo Yes/No
   NCycle integer
   XC integer
End

NewResponseSCF

Type: Block
Description: Details for the linear-response self-consistent optimization cycle. Only influencing the NewResponse code.

Bootstrap

Type: Integer
Default value: 0
Description: defines if the Berger2015 kernel (Bootstrap 1) is used or not (Bootstrap 0). If you chose the Berger2015 kernel, you have to set NewResponseSCF%XC to ‘0’. Since it shall be used in combination with the bare Coulomb response only. Note: The evaluation of response properties using the Berger2015 is recommend for 3D systems only!

COApproach

Type: Bool
Default value: Yes
Description: The program automatically decides to calculate the integrals and induced densities via the Bloch expanded atomic orbitals (AO approach) or via the cyrstal orbitals (CO approach). The option COApproach overrules this decision.

COApproachBoost

Type: Bool
Default value: No
GUI name: CO Approach Boost
Description: Keeps the grid data of the Crystal Orbitals in memory. Requires significantly more memory for a speedup of the calculation. One might have to use multiple computing nodes to not run into memory problems.

Criterion

Type: Float
Default value: 0.001
Description: For the SCF convergence the RMS of the induced density change is tested. If this value is below the Criterion the SCF is finished. Furthermore, one can find the calculated electric susceptibility for each SCF step in the output and can therefore decide if the default value is too loose or too strict.

DIIS

Type: Block
Description: Parameters influencing the DIIS self-consistency method

Enabled

Type: Bool
Default value: Yes
Description: If not enabled simple mixing without DIIS acceleration will be used.

MaxSamples

Type: Integer
Default value: 10
Description: Specifies the maximum number of samples considered during the direct inversion of iteration of subspace (DIIS) extrapolation of the atomic charges during the SCC iterations. A smaller number of samples potentially leads to a more aggressive convergence acceleration, while a larger number often guarantees a more stable iteration. Due to often occurring linear dependencies within the set of sample vectors, the maximum number of samples is reached only in very rare cases.

MaximumCoefficient

Type: Float
Default value: 10.0
Description: When the diis expansion coefficients exceed this threshold, the solution is rejected. The vector space is too crowded. The oldest vector is discarded, and the expansion is re-evaluated.

MinSamples

Type: Integer
Default value: -1
Description: When bigger than one, this affects the shrinking of the DIIS space on linear dependence. It will not reduce to a smaller space than MinSamples unless there is extreme dependency.

MixingFactor

Type: Float
Default value: 0.2
Description: The parameter used to mix the DIIS linear combination of previously sampled atomic charge vectors with an analogous linear combination of charge vectors resulting from population analysis combination. It can assume real values between 0 and 1.

LowFreqAlgo

Type: Bool
Default value: Yes
GUI name: Low Frequency Algorithm
Description: Numerically more stable results for frequencies lower than 1.0 eV. Note: for a graphene monolayer the conical intersection results in a very small band gap (zero band gap semi-conductor). This leads ta a failing low frequency algorithm. One can then chose to use the algorithm as originally proposed by Kootstra by setting the input value to *false*. But, this can result in unreliable results for frequencies lower than 1.0 eV!

NCycle

Type: Integer
Default value: 20
GUI name: Cycles
Description: Number of SCF cycles for each frequency to be evaluated.

XC

Type: Integer
Default value: 1
Description: Influences if the bare induced Coulomb response (XC 0) is used for the effective, induced potential or the induced potential derived from the ALDA kernel as well (XC 1).

NewResponseKSpace
   Eta float
   SubSimp integer
End

NewResponseKSpace

Type: Block
Description: Modify the details for the integration weights evaluation in reciprocal space for each single-particle transition. Only influencing the NewResponse code.

Eta

Type: Float
Default value: 1e-05
Description: Defines the small, finite imaginary number i*eta which is necessary in the context of integration weights for single-particle transitions in reciprocal space.

SubSimp

Type: Integer
Default value: 3
Description: determines into how many sub-integrals each integration around a k point is split. This is only true for so-called quadratic integration grids. The larger the number the better the convergence behavior for the sampling in reciprocal space. Note: the computing time for the weights is linear for 1D, quadratic for 2D and cubic for 3D!

OldResponse¶

OldResponse
   Berger2015 Yes/No
   CNT Yes/No
   CNVI float
   CNVJ float
   Ebndtl float
   Enabled Yes/No
   Endfr float
   Isz integer
   Iyxc integer
   NewVK Yes/No
   Nfreq integer
   QV Yes/No
   Shift float
   Static Yes/No
   Strtfr float
End

OldResponse

Type: Block
Description: Options for the old TD-CDFT implementation.

Berger2015

Type: Bool
Default value: No
Description: Use the parameter-free polarization functional by A. Berger (Phys. Rev. Lett. 115, 137402). This is possible for 3D insulators and metals. Note: The evaluation of response properties using the Berger2015 is recommend for 3D systems only!

CNT

Type: Bool
Description: Use the CNT parametrization for the longitudinal and transverse kernels of the XC kernel of the homogeneous electron gas. Use this in conjunction with the NewVK option.

CNVI

Type: Float
Default value: 0.001
Description: The first convergence criterion for the change in the fit coefficients for the fit functions, when fitting the density.

CNVJ

Type: Float
Default value: 0.001
Description: the second convergence criterion for the change in the fit coefficients for the fit functions, when fitting the density.

Ebndtl

Type: Float
Default value: 0.001
Unit: Hartree
Description: the energy band tolerance, for determination which routines to use for calculating the numerical integration weights, when the energy band posses no or to less dispersion.

Enabled

Type: Bool
Default value: No
Description: If true, the response function will be calculated using the old TD-CDFT implementation

Endfr

Type: Float
Default value: 3.0
Unit: eV
Description: The upper bound frequency of the frequency range over which the dielectric function is calculated

Isz

Type: Integer
Default value: 0
Description: Integer indicating whether or not scalar zeroth order relativistic effects are included in the TDCDFT calculation. 0 = relativistic effects are not included, 1 = relativistic effects are included. The current implementation does NOT work with the option XC%SpinOrbitMagnetization equal NonCollinear

Iyxc

Type: Integer
Default value: 0
Description: integer for printing yxc-tensor (see http://aip.scitation.org/doi/10.1063/1.1385370). 0 = not printed, 1 = printed.

NewVK

Type: Bool
Description: Use the slightly modified version of the VK kernel (see https://aip.scitation.org/doi/10.1063/1.1385370). When using this option one uses effectively the static option, even for metals, so one should check carefully the convergence with the KSPACE parameter.

Nfreq

Type: Integer
Default value: 5
Description: the number of frequencies for which a linear response TD-CDFT calculation is performed.

QV

Type: Bool
Description: Use the QV parametrization for the longitudinal and transverse kernels of the XC kernel of the homogeneous electron gas. Use this in conjunction with the NewVK option. (see reference).

Shift

Type: Float
Default value: 0.0
Unit: eV
Description: energy shift for the virtual crystal orbitals.

Static

Type: Bool
Description: An alternative method that allows an analytic evaluation of the static response (normally the static response is approximated by a finite small frequency value). This option should only be used for non-relativistic calculations on insulators, and it has no effect on metals. Note: experience shows that KSPACE convergence can be slower.

Strtfr

Type: Float
Default value: 1.0
Unit: eV
Description: is the lower bound frequency of the frequency range over which the dielectric function is calculated.

References

1: F. Kootstra, P.L. de Boeij and J.G. Snijders, Efficient real-space approach to time-dependent density functional theory for the dielectric response of nonmetallic crystals. Journal of Chemical Physics 112, 6517 (2000).
2: P. Romaniello and P.L. de Boeij, Time-dependent current-density-functional theory for the metallic response of solids. Physical Review B 71, 155108 (2005).
3: J.A. Berger, P.L. de Boeij and R. van Leeuwen, Analysis of the viscoelastic coefficients in the Vignale-Kohn functional: The cases of one- and three-dimensional polyacetylene., Physical Review B 71, 155104 (2005).
4: P. Romaniello and P.L. de Boeij, Relativistic two-component formulation of time-dependent current-density functional theory: application to the linear response of solids., Journal of Chemical Physics 127, 174111 (2007).