TD-CDFT Response Properties For Crystals (OldResponse)

BAND can calculate response properties such as the frequency-dependent dielectric function within the theoretical framework of time-dependent current density function theory (TD-CDFT).

This introductory tutorial will show you how to:

  • Set up and run a BAND single point calculation (using AMSjobs and AMSinput)

  • Set up and run a BAND TD-CDFT, linear response calculation (using AMSjobs and AMSinput) with the OldResponse method

  • Visualize the dielectric function using AMSspectra

If you are not at all familiar with our Graphical User Interface (GUI), check out the Introductory tutorial first.

Step 1: Create the system

We now want to create a silicon crystal. Let us import the geometry from our database of structures:

1. Open AMSinput.
2. Switch to BAND: ADFPanel → BANDPanel
3. Search for Silicon in the search box Search.
4. Select Crystals → Si. (you have to click on the triangle to the right of Crystals to expand the list)
5. click on View → Periodic → Periodic View Type → Repeat Unit Cell
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step1.png

Step 2: Run a Single Point Calculation (LDA)

We will first perform a single-point calculation of our Silicon crystal using LDA.

Tip

It is good practice to do a convergence study w. r. t. k-space sampling and basis set.

1. Select the ‘BAND Main’ panel.
2. Change Basis set to DZP.
3. Check the PDOS and Band structure boxes.
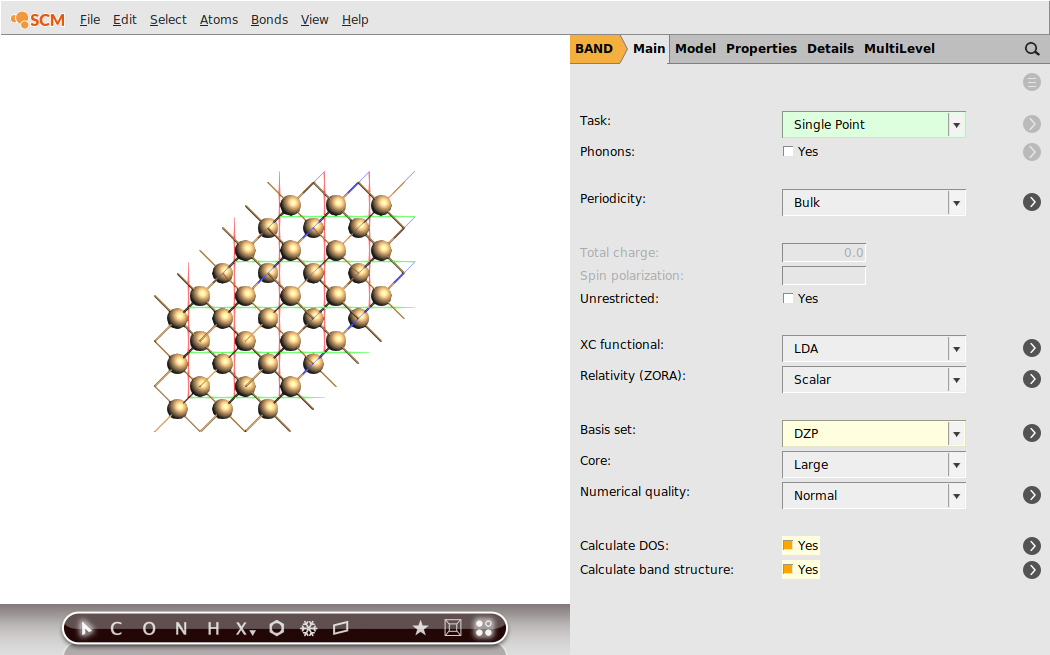
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step2_Int1.png
4. Go to Details → K-Space Integration
5. Set the K-Space grid type option to Symmetric
6. Set the Accuracy to 3.
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step2_Int2.png
7. File → Save As…, use name LDA_SP.ams
8. File → Run

After the calculation finished, we can check the band-gap energy e.g. in the logfile. Furthermore, with the help of the AMSbandstructure module we can validate that a very basic property is reproduced by this rather poor k-space sampling - Si diamond has an indirect band-gap.

9. SCM → Logfile
10. SCM → Band Structure
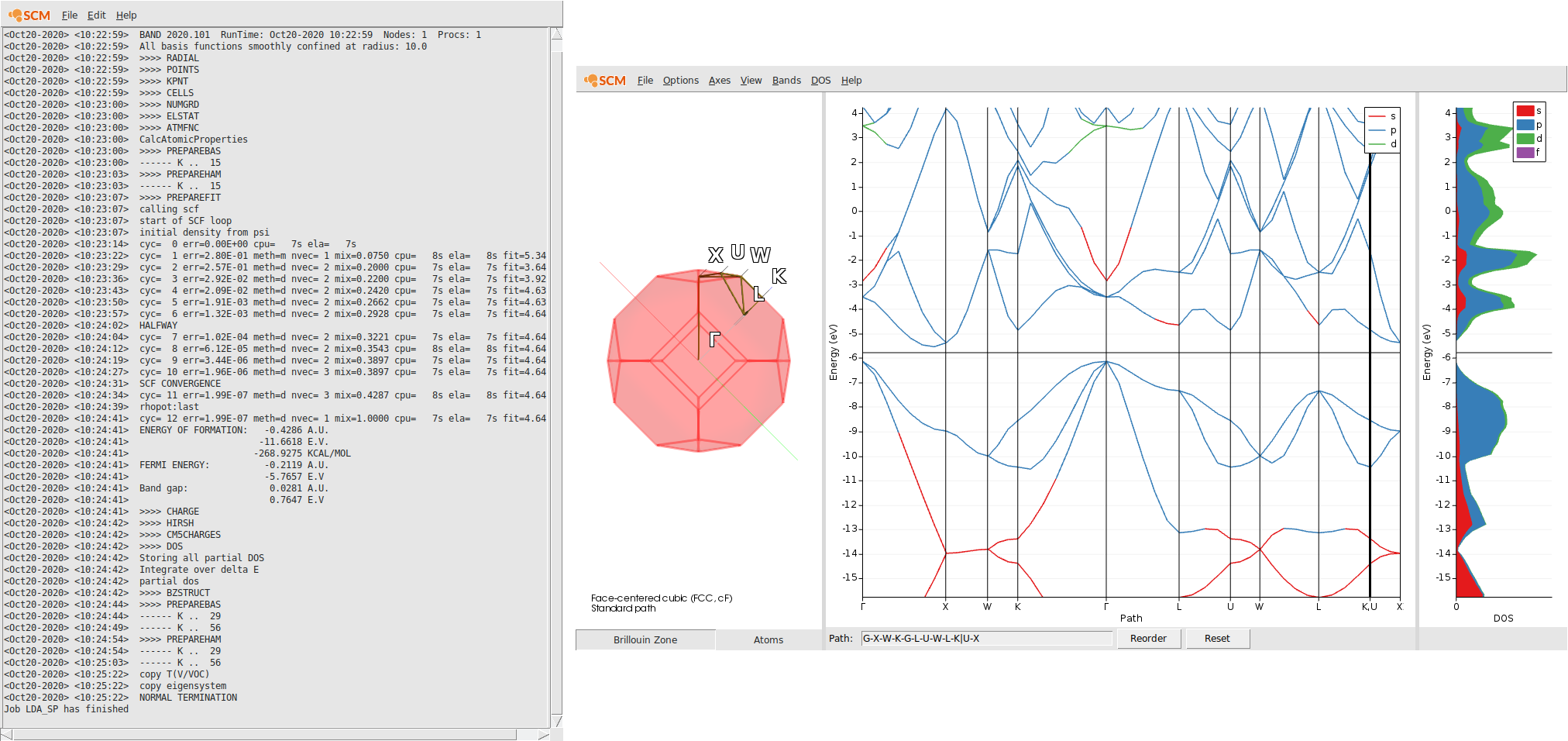
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step2_Int3.png

Step 3: Run an OldResponse Calculation (ALDA)

We will now calculate the frequency-dependent dielectric function using linear response TD-CDFT.

In the previous step we learned that the calculated band-gap for the chosen theoretical level is 0.76 eV. This is 0.35 eV below the experimental band-gap. Hence, we will shift the virtual crystal orbitals by this value in energy space. We will sample the frequency range from 2.0 eV to 5.0 eV with a step-size of 0.1 eV.

1. Go to the ‘BAND Main’ panel and un-tick the Bandstructure and DOS check-boxes.
2. Go to Properties → Dielectric Function (TD-CDFT).
3. Change Method to OldResponse.
4. Change Number of frequencies to 31.
5. Change Starting frequency to 2.0.
6. Change End frequency to 5.0.
7. Change Shift to 0.35.
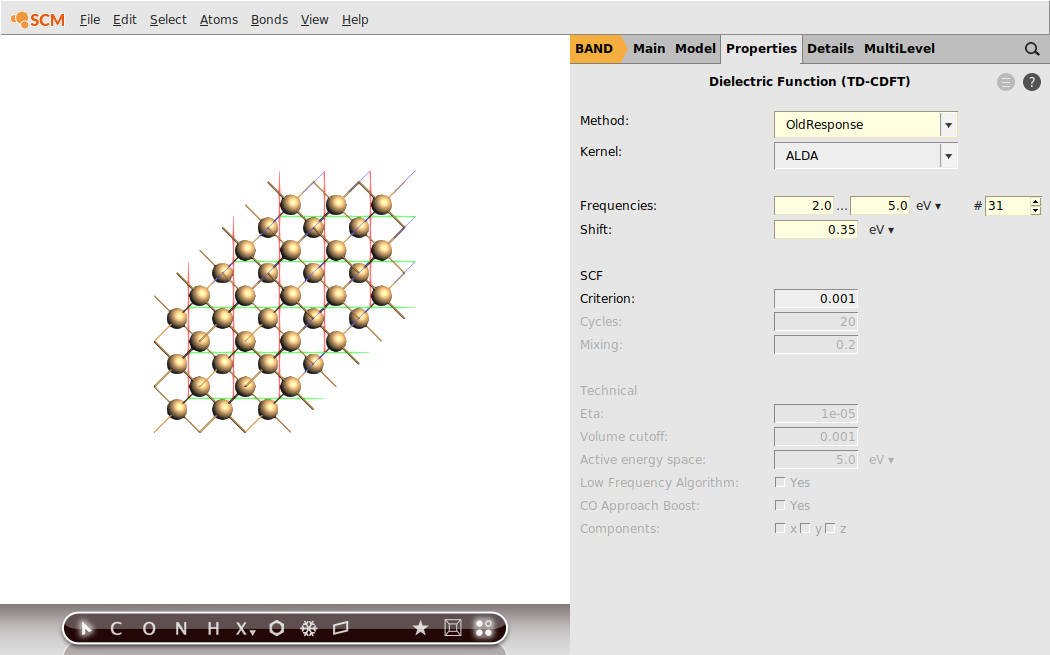
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step3_Int1.png
8. File → Save As…, use name LDA_TDCDFT.ams
9. File → Run

After the calculation finished, we can visualize the dielectric function using AMSspectra.

10. SCM → Spectra
11. Spectra → TD-CDFT → Dielectric Function → XX
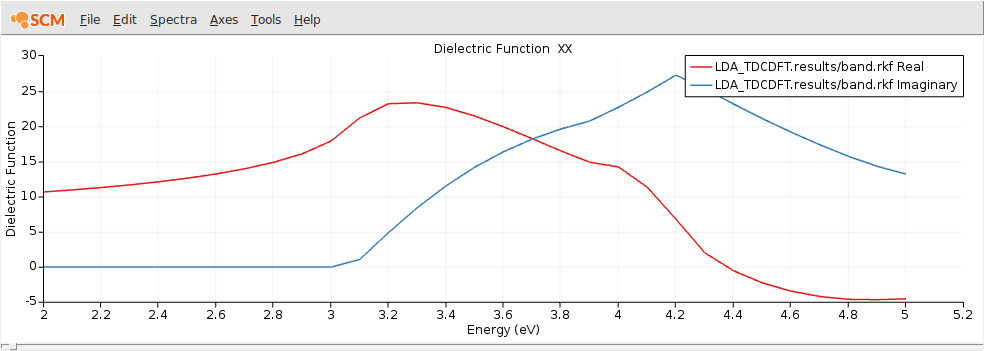
/scm-uploads/doc/Tutorials/_images/TDCDFT_SiBulk_Step3_Int2.png

The general features of the frequency-dependent dielectric function are nicely reproduced, but for a quantitatively better result one has to converge the k-space sampling, basis set and numerical integration. Also switching to the Berger2015 kernel would improve the results further. [Ref]