Plasmon Enhanced Two Photon Absorption

Two photon absorption (TPA) is an excitation process in which two photons simultaneously transfer their energy to an absorbing molecule or material. The excitation of the electronic structure of the absorbing system thereby happens as a single process.

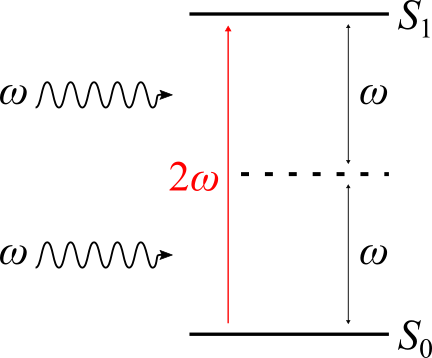
/scm-uploads/doc/Tutorials/_images/adf_TPA_levels.png

Fig. 42 Schematics of the levels involved in a two photon absorption (TPA) process exciting an absorbing system from its ground state \(S_{0}\) to an excited state \(S_{1}\).

This leads to an excitation of the absorbing material without the population of any intermediate excited state. Like most nonlinear optical phenomena, TPA processes have very small cross sections and are therefore relevant at very high light intensities only. Nonetheless, many potential applications of TPA phenomena in intense laser fields have been suggested, ranging from photochemistry over microfabrication to medical imaging.

These applications are of course only feasible in conjunction with absorbing materials that exhibit a large enough TPA cross sections. Apart from using dyes which are specifically taylored for specific TPA applications, TPA cross sections are enhanced significally by plasmonic resonances with nearby metallic nanoparticles. This tutorial shows how such plasmon-enhanced TPA (PETPA) processes can be studied with ADF and is based on the following publication:

Z. Hu and L. Jensen A Discrete Interaction Model/Quantum Mechanical Method for Simulating Plasmon-Enhanced Two-Photon Absorption, J. Chem. Theory Comput. 14, 5896-5903 (2018).

To make the computations feasible within the framework of a tutorial, the TPA cross section plasmon-enhancement factor is computed for a single frequency only.

Model and Methods

In non-linear optics the response of a molecular system to an external electric field \(E\) can be described in terms of a series expansion of the induced dipole

\[\mu_{i}^{\mathrm{ind}} = \alpha_{ij}E_{j} + \frac{1}{2}\beta_{ijk}E_{j}E_{k} + \frac{1}{6}\gamma_{ijkl}E_{j}E_{k}E_{l} + \dots\]

In the case of oscillating electromagnetic fields of photons, the above susceptibility tensors become frequency dependent and are commonly denoted as \(\alpha(-\!\omega_{a}; \omega_{a})\), \(\beta(-\!\omega_{a}\!-\!\omega_{b}; \omega_{a}, \omega_{b})\), \(\gamma(-\!\omega_{a}\!-\!\omega_{b}\!-\!\omega_{c}; \omega_{a}, \omega_{b}, \omega_{c})\) etc. Note that each of these tensors, in combination with certain sign patterns and values for \(\omega_{a}\), \(\omega_{b}\) etc., corresponds to different optical properties.

In many practical situations one can assume all photons to be of the same frequency, i.e. \(\omega_{a} = \omega_{b} = \omega_{c} = \omega\). In the case of such a degenerate TPA, a frequency dependent second hyperpolarizability of the form \(\gamma(-\omega; \omega, \omega, -\omega)\) describes the simultaneous absorption of two photons, each with a frequency of \(\omega\).

The calculation of TPA and other non-linear optical processes is implemented in ADFs AORESPONSE module and utilizes TDDFT as well as the the 2n+1 rule to perturbatively compute the required cubic response properties; see the corresponding manual section for more details on the calculation of TPA and similar nonlinear optical phenomena. This implementation in ADF allows for the computation of the 81 real and imaginary entries of the tensor \(\gamma\) for a given frequency \(\omega\). Afterwards, the TPA cross section can be computed from the imaginary part of \(\gamma(-\omega; \omega, \omega, -\omega)\) as follows:

\[\sigma_{\mathrm{TPA}}(\omega) = \frac{N\pi^{3}\hbar^{3}\alpha_{\mathrm{f}}^{2}}{15e^{4}}\sum\limits_{ij}\mathrm{Im}\!\left\{\gamma_{iijj}(-\omega; \omega, \omega, -\omega)+\gamma_{ijji}(-\omega; \omega, \omega, -\omega)+\gamma_{ijij}(-\omega; \omega, \omega, -\omega)\right\}\]

To obtain an entire spectrum for \(\sigma_{\mathrm{TPA}}(\omega)\) the ADF calculation is repeated while varying the frequency \(\omega\) (see the aforementioned script).

This tutorial examines the PETPA properties of para-Nitroaniline (p-NA), whose NH2-donor and NO2-acceptor groups make it a typical push-pull molecule with charge-transfer excitations and thus, amenable to PETPA processes.

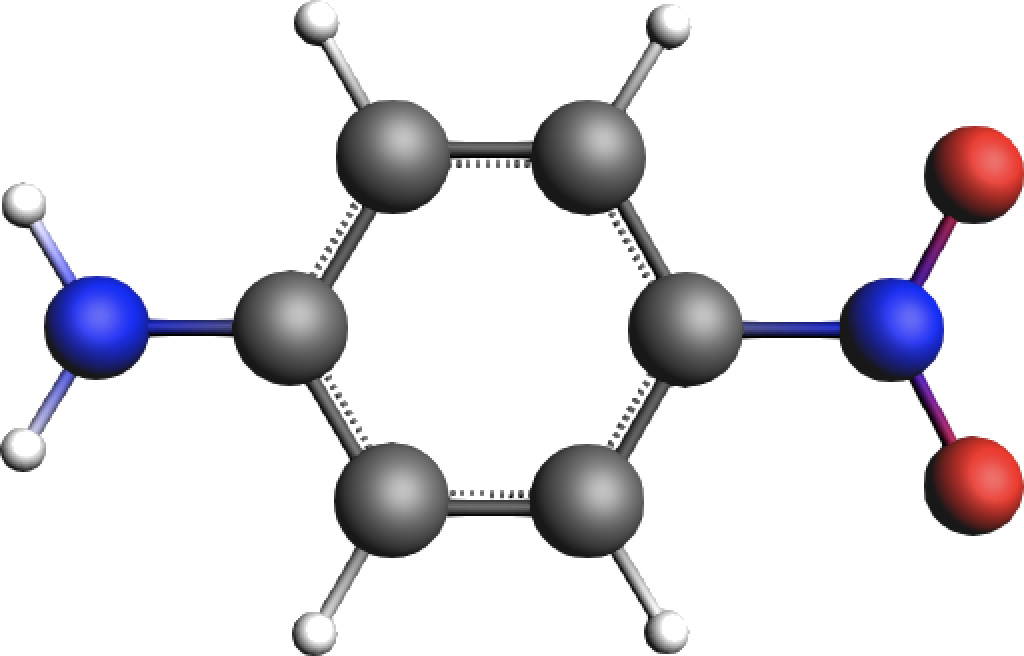
/scm-uploads/doc/Tutorials/_images/adf_TPA_pNA.png

Fig. 43 para-Nitroaniline (p-NA) with an electron donating NH2 moiety and an electron withdrawing NO2 group

We thereby focus on the TPA resonance at \(\omega =\) 1.71 eV (see Figure 1 in the original study) and compute the corresponding cross section.

To simulate the plasmon enhancement of this resonance, the p-NA molecule is placed in the junction between two icosahedral Ag2057 nanoparticles.

/scm-uploads/doc/Tutorials/_images/adf_TPA_pNA_Ag4114.png

Fig. 44 para-Nitroaniline molecule in the junction between two Ag2057 clusters

While the p-NA molecule is still treated with a quantum mechanical TDDFT description, the additional Ag2057 clusters are represented by a polarizability interaction model (PIM). PIM describes the interaction between atoms in terms of frequency dependent induced dipoles which is a sufficient representation of the plasmonic near field emerging during the PETPA process. The DIM-QM manual section provides further information on PIM and similar embedding models.

Workflow and Calculation Script

A scripted workflow to compute the TPA plasmon enhancement of the p-NA resonance at \(\omega =\) 1.71 eV can be obtained here. The archive PETPA_Spectrum.zip thereby contains four individual files

pNA.xyz

Structure of the para-Nitroaniline molecule as obtained from an optimization at the BP86/TZP level

Ag2057.xyz

Structure of a single icosahedral Ag2057 cluster model with an Ag-Ag distance of 299 pm

Ag_jc

PIM parameters: wavelength-dependent dielectric constants and refractive indices

PETPA_Spectrum.py

The main script based on the PLAMS scripting environment; The workflow in this file will be detailed below.

The main script starts by importing necessary external modules, initializing PLAMS and defining the other three files needed for this workflow:

######################### Initializations ##########################
import os, sys
import numpy as np
from scm.plams import *
init()


############################ Filenames #############################
geometryFileQM   = 'pNA.xyz'
geometryFileDIM  = 'Ag2057.xyz'
parameterFileDIM = 'Ag_jc'

The TPA cross sections obtained from the second hyperpolarizabilities have to be converted from atomic units into units of Göppert-Mayer (1 GM = 10−50 cm4 s / photon):

######################### Unit Conversion ##########################
# conversion a.u. to GM i.e. to 10E-50 * cm^4 * s / photon
au2GM    = 1.896831653271693 # = 5.2918e-9**4 * 2.418884326505E-17 * 1.0E50
alphaf   = 0.0072973525664
factorGM = au2GM * 4 * np.pi**3 * alphaf**2 / 15

In the next step the molecular models are defined. First, an instance of the PLAMS Molecule class named molQM is initialized with the structure from pNA.xyz. The N-atoms of this model are aligned with the z-axis and have the same distance (~2.84 Å) from the origin.

This is followed by analogously initializing the Molecule object dimRegionL with the structure of a single cluster unit. This Ag2057 structure is aligned around the z-axis with its uppermost Ag-atom at the origin. The cluster is then shifted to have the appropriate distance (4Å, see the original paper) from the lower N-atom of the p-PNA molecule. The second cluster is first obtained by copying the dimRegionL object, followed by a 180° rotation in the xz-plane to put it into the right position, 4Å away from the upper N-atom of the p-NA molecule:

############################## Models ##############################
# Load structure of the QM region
molQM = Molecule(geometryFileQM)

# Generate the DIM region, load and shift one cluster, then rotate its copy and merge both parts into a single molecule instance
dimRegionL = Molecule(geometryFileDIM)
dimRegionL.translate((.0, .0, -4.-2.81396650))
dimRegionU = dimRegionL.copy()
dimRegionU.rotate([-1., .0, .0, .0, 1., .0, .0, .0, -1])
dimRegion = dimRegionL + dimRegionU

Next the input segment for the DFT calculations are defined in the form of the PLAMS settings object. A TZP all-electron basis set is used to properly represent the excitations during the TPA process. Due to its correct long-range behavior the SAOP model potential is used to describe exchange correlation interactions. The block aoresponse defines the task of computing the \(\gamma^{\mathrm{TPA}}\) tensor at the frequency of \(\omega =\) 1.71 eV. If you want to produce an entire spectrum for a rance of incident frequencies, you may uncomment the second line starting with omegas. Note however, that this will take a lot of computational time. For technical reasons an excited state lifetime parameter of \(\Gamma =\) 0.0037 a.u. is defined.

########################## DFT-Settings #############################
# QM Settings
setQM = Settings()
setQM.input.ams.Task                   = 'SinglePoint'
setQM.input.adf.basis.type             = 'TZP'
setQM.input.adf.basis.core             = 'None'
setQM.input.adf.xc.model               = 'SAOP'
setQM.input.adf.symmetry               = 'nosym'
setQM.input.adf.allpoints              = ''
setQM.input.adf.numericalquality       = 'good'

# Just a single frequency of 1.71 eV:
omegas                                 = [ 1.71 ]
# Alternatively an entire spectrum:
#omegas                                = np.linspace(0.864, 2.48, num=20)
setQM.input.adf.aoresponse.scf         = 'iterations 50'
setQM.input.adf.aoresponse.gamma       = ''
setQM.input.adf.aoresponse.tpa         = ''
setQM.input.adf.aoresponse.ALDA        = ''
setQM.input.adf.aoresponse.lifetime    = '0.0037'

Further information on how to set up such inputs blocks can be found in the corresponding section of the PLAMS manual.

The PIM embedding is defined by two input blocks. DIMQM specifies the model itself along with several technical parameters. The second block, DIMPAR contains the definition of the actual PIM region. First, the parameters for the Ag-atoms are defined by specifying the corresponding atomic radius followed by loading the parameter file Ag_jc. The structure of the PIM region is then added by copying the symbols and coordinates of the Ag-atoms in the clusters from previously generated the dimRegion object.

########################## PIM-Settings #############################
# DIM Settings, generates the blocks DIMQM and DIMPAR
setDIM = Settings()
setDIM.input.adf.DIMQM.PIM        = ''
setDIM.input.adf.DIMQM.ALGORITHM  = 'Direct'
setDIM.input.adf.DIMQM.NITER      = '2000'
setDIM.input.adf.DIMQM.FREQUENCY  = ''
setDIM.input.adf.DIMQM.LOCALFIELD = ''

setDIM.input.adf.DIMPAR['_1']     = 'Ag'
setDIM.input.adf.DIMPAR['_2']     = 'rad = 1.4445'
setDIM.input.adf.DIMPAR['_3']     = 'exp '+ os.path.join(os.path.dirname(os.path.abspath(__file__)), parameterFileDIM)
setDIM.input.adf.DIMPAR['_4']     = 'SUBEND'
setDIM.input.adf.DIMPAR['_5']     = 'XYZ'
setDIM.input.adf.DIMPAR['_6']     = len(dimRegion)
for iAt, atom in enumerate(dimRegion):
   setDIM.input.adf.DIMPAR[f'_{7+iAt}'] = atom.str()
setDIM.input.adf.DIMPAR[f'_{7+len(dimRegion)}'] = 'SUBEND'

The actual calculations are enclosed in a loop over the incident frequencies. This is necessary in case you chose earlier to calculate the entire spectrum. Inside the loop we also put the incident frequency we defined earlier into the aoresponse block in the input. Note, that the three individual frequencies of \(\gamma(-\omega; \omega, \omega, -\omega)\) have to be specified separately. After all input options are defined, the TPA and PETPA calculations can start. First the TPA calculation of p-NA in vacuum is invoked by defining an AMSJob object without using the settings of the PIM embedding. After running the job, the values of the \(\gamma^{\mathrm{TPA}}\) tensor are extracted from the output file by using the grep_output method of the PLAMS Results class. The TPA cross section is then obtained by using the conversion factors specified above. The same steps are repeated for the PETPA calculation for which the setDIM object is now added in the initialization of the AMSJob object. At the end of the workflow the results are printed and the PLAMS environment is shut down.

### Loop over frequencies and calculate PETPA enhancement factors ###
spectrum = [('omega', 'sigma(TPA)', 'sigma(PETPA)', 'enhancement')]
for omega in omegas:
    setQM.input.adf.aoresponse.Frequencies = f"{omega} {omega} {-omega}"

    ################### Calculate TPA Cross Sections ####################
    # Setup and run TPA job without DIM environment
    jobTPA         = AMSJob(name=f'TPA_{omega}eV', molecule=molQM, settings=setQM)
    resultsTPA     = jobTPA.run()
    gammaImagTPA   = np.array([float(elem.split()[-1]) for elem in resultsTPA.grep_output(pattern=' gamma                             real              imaginary', options='-A81')[1:]]).reshape((3,3,3,3))
    sigmaTPA       = factorGM * Units.convert(omega,'eV','au')**2 * sum(gammaImagTPA[i][i][j][j] + gammaImagTPA[i][j][j][i] + gammaImagTPA[i][j][i][j] for i in range(3) for j in range(3))

    # Setup and run PETPA job with DIM environment
    jobPETPA       = AMSJob(name=f'PETPA_{omega}eV', molecule=molQM, settings=setQM+setDIM)
    resultsPETPA   = jobPETPA.run()
    gammaImagPETPA = np.array([float(elem.split()[-1]) for elem in resultsPETPA.grep_output(pattern=' gamma                             real              imaginary', options='-A81')[1:]]).reshape((3,3,3,3))
    sigmaPETPA     = factorGM * Units.convert(omega,'eV','au')**2 * sum(gammaImagPETPA[i][i][j][j] + gammaImagPETPA[i][j][j][i] + gammaImagPETPA[i][j][i][j] for i in range(3) for j in range(3))

    ######################## Gather Results #############################
    spectrum.append((omega, sigmaTPA, sigmaPETPA, sigmaPETPA/sigmaTPA))
    print('omega          = ',  omega, 'eV')
    print('gammaI(TPA)    =\n', gammaImagTPA)
    print('gammaI(PETPA)  =\n', gammaImagPETPA)
    print('sigma(TPA)     = ',  sigmaTPA, 'GM')
    print('sigma(PETPA)   = ',  sigmaPETPA, 'GM')
    sys.stdout.flush()


######################## Print Final Results ########################
for omega, sigmaTPA, sigmaPETPA, enhancement in spectrum:
   print(omega, sigmaTPA, sigmaPETPA, enhancement)

finish()

Calculation and Results

The PLAMS script can be invoked from the command line by typing:

$AMSBIN/amspython PETPA_Spectrum.py

The total runtime of the workflow can be expected to be between one and two hours per incident frequency, depending on the computing hardware used. After its completion, the results can be examined.

The \(\gamma^{\mathrm{TPA}}\) values are printed towards the end of the output file of ADF. For the results of the TPA calculation with \(\omega =\) 1.71 eV these values read as follows:

TPA SECOND HYPERPOLARIZABILITY
Frequency1  =  0.6284135000E-01 Hartrees
Frequency2  =  0.6284135000E-01 Hartrees
Frequency3  = -0.6284135000E-01 Hartrees
Lifetime    =  0.3700000000E-02 Hartrees
------------------------------------------
Second hyperpolarizability tensor:
                               X              Y              Z
X        X        X       962.3555         0.0001         0.0006
                  Y        -0.0003      1458.9202        -0.0002
                  Z        -0.0003        -0.0002      2408.0616

X        Y        X        -0.0003      1458.9202        -0.0002
                  Y       115.1999         0.0006         0.0031
                  Z         0.0058         0.0000        -0.0002

X        Z        X        -0.0003        -0.0002      2408.0616
                  Y         0.0058         0.0000        -0.0002
                  Z     -2406.8058        -0.0062        -0.0512

Y        X        X         0.0001       176.1401        -0.0048
                  Y      1458.9200        -0.0020         0.0001
                  Z        -0.0002        -0.0018         0.0006

Y        Y        X      1458.9200        -0.0020         0.0001
                  Y         0.0006      4452.8844        -0.0313
                  Z         0.0000         0.0355      2000.4493

Y        Z        X        -0.0002        -0.0018         0.0006
                  Y         0.0000         0.0355      2000.4493
                  Z        -0.0062    -13277.4347         0.4869

Z        X        X         0.0006        -0.0048     -2975.6626
                  Y        -0.0002        -0.0000         0.0335
                  Z      2408.0590        -0.0009         0.0292

Z        Y        X        -0.0002        -0.0000         0.0335
                  Y         0.0031        -0.0305    -10866.7839
                  Z        -0.0002      2000.5211        -0.6172

Z        Z        X      2408.0590        -0.0009         0.0292
                  Y        -0.0002      2000.5211        -0.6172
                  Z        -0.0512         0.4907    198873.2621
----------------------------------------------------
     IMAGINARY SECOND HYPERPOLARIZABILITY
----------------------------------------------------
                             X              Y              Z
X        X        X       196.9736         0.0003         0.0011
                  Y         0.0002        23.6022        -0.0001
                  Z         0.0011         0.0001        49.6052

X        Y        X         0.0002        23.6022        -0.0001
                  Y      1202.2980         0.0021         0.0070
                  Z        -0.0199         0.0000         0.0000

X        Z        X         0.0011         0.0001        49.6052
                  Y        -0.0199         0.0000         0.0000
                  Z    -18625.6335        -0.0336        -0.1083

Y        X        X         0.0004      1191.1904        -0.0066
                  Y        23.5294         0.0014         0.0000
                  Z         0.0001         0.0075         0.0001

Y        Y        X        23.5294         0.0014         0.0000
                  Y         0.0021      7588.8550        -0.0426
                  Z         0.0000        -0.1251       102.1879

Y        Z        X         0.0001         0.0075         0.0001
                  Y         0.0000        -0.1251       102.1879
                  Z        -0.0336   -117409.6225         0.6436

Z        X        X         0.0011        -0.0066    -18628.5531
                  Y        -0.0001        -0.0000        -0.0209
                  Z        48.7078        -0.0001        -0.1166

Z        Y        X        -0.0001        -0.0000        -0.0209
                  Y         0.0070        -0.0421   -117819.0314
                  Z         0.0000        94.7464         1.9250

Z        Z        X        48.7078        -0.0001        -0.1166
                  Y         0.0000        94.7464         1.9250
                  Z        -0.1083         0.6472   1839140.3016
----------------------------------------------------

Note the large values for \(\gamma^{\mathrm{TPA}}_{zzzz}\) that indicate a large propensity for TPA in z-direction. Because the donor and acceptor groups of p-NA are aligned with the z-axis, large \(\gamma^{\mathrm{TPA}}_{zzzz}\) values are to be expected. Even larger values are obtained in the case of PETPA.

From the output of the workflow script we then obtain a cross section of \(\sigma^{\mathrm{TPA}} =\) 17.39 GM, which is close to the result of 16 from the original paper. The corresponding \(\sigma^{\mathrm{PETPA}}\) value is found to be 1695.33 GM, which results in a plasmon enhancement factor of 97.