PolTDDFT: damped complex polarizabilities Au₁₂

In this Tutorial we calculate the absorption spectrum of Au₁₂ using PolTDDFT, which is a fast algorithm to solve the TD-DFT equations. We will look at some of the analysis options that PolTDDFT has to offer, like the so called individual component maps of oscillatory strength (ICM-OS, see Ref. 1), transition contribution maps (TCM), and an analysis of the spectra per region, using the fragment projection analysis approach (see Ref. 2).

Note

See also the webinar by Mauro Stener regarding PolTDDFT

Set calculation options

For PolTDDFT it very important is to use specially made auxiliary fit sets. Here we will use the POLTDDFT/DZ frozen core basis set for Au. The model exchange-correlation potential LB94 will be used, which is often used in PolTDDFT calculations. LB94 has an asymptotically correct Coulomb tail and is thus superior to purely gradient-corrected xc-functionals (such as PBE) in describing low-lying unoccupied electronic states.

In order to use the region analysis option we divide Au₁₂ in 2 regions: the 3 inner gold atoms in one region and the other 9 in another region.

Start AMSinput.

Obtain Au₁₂ by copy-pasting the following coordinates into AMSinput:

Au       3.90924307       1.34478417       0.00000000
Au       1.60055482       2.77224227       0.00000000
Au      -0.79000428       4.05789589       0.00000000
Au      -3.11923879       2.71311172       0.00000000
Au      -0.77594464       1.34397554       0.00000000
Au       1.55188928      -0.00000000       0.00000000
Au       3.90924307      -1.34478417       0.00000000
Au       1.60055482      -2.77224227       0.00000000
Au      -0.77594464      -1.34397554       0.00000000
Au      -3.20110964      -0.00000000       0.00000000
Au      -3.11923879      -2.71311172       0.00000000
Au      -0.79000428      -4.05789589       0.00000000

Use the panel bar Model → Regions

Select the 3 inner gold atoms

Click the button to add a region, and rename Region_1 to Au3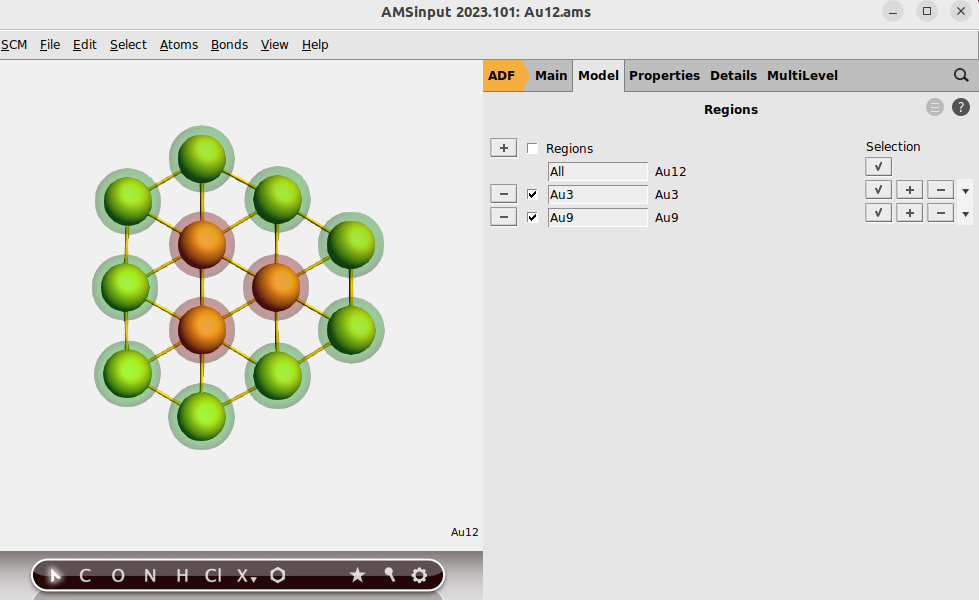

Select → Invert Selection

Add a region, and rename Region_2 to Au9

Use the Main panel

XC functional → Model → LB94

Basis set → POLTDDFT → POLTDDFT/DZ

Use the panel bar Properties → POLTDDFT

Check the ‘UV/Vis and CD spectrum’ checkbox

Check the ‘Analysis’ checkbox

Check the ‘Region analysis’ checkbox

We are now ready to run the calculation.

Save your input as Au12 using File → Save As….

Run the calculation with File → Run.

Wait for the calculation to finish.

Results

Once the PolTDDFT calculation has finished, the absorption spectrum can be viewed.

Open → Spectra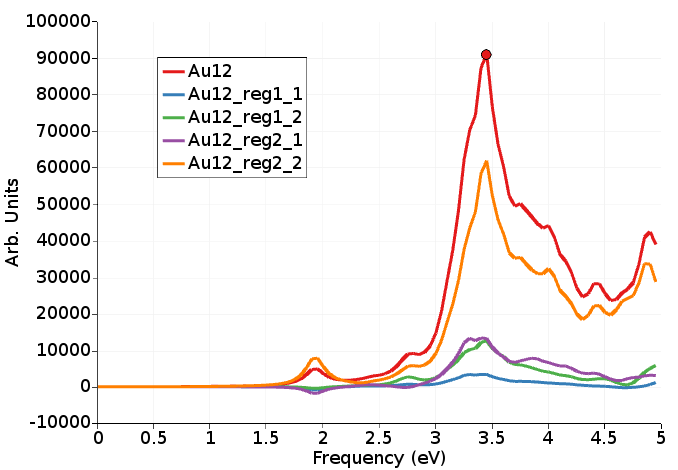

Here we see an analysis of the absorption spectrum per region, using the fragment projection analysis approach (see Ref. 2). The most important part comes from region Au9 -> region Au9 (orange, Au12_reg2_2), which is not unexpected because there are more atoms in region Au9 than in region Au3, but it is larger than expected (expected is around (9*9)/(12*12)=56%).

Right of the absorption spectrum one can find a two-dimensional ICM-OS plot for the X component. If one selects the highest peak (point 70 at 3.45 eV) in the absorption spectrum the ICM-OS plot for the X component at frequency 3.45 eV will be shown. Next one can select the TCM plot for the X component at frequency 3.45 eV. Of course, for a full analysis at a certain frequency one should also look at the Y and Z component. Here, due to symmetry, the Y component will give the same information as the X component. The contributions to the oscillator strength from the Z component are small.

Select the AMSspectra window

Select point 70 (frequency 3.45 eV) in the table below the absorption spectrum

Under the right figure make sure that ‘icm-os’ and ‘x’ are selected

Next select ‘tcm’ and ‘x’ and press the ‘Update’ button

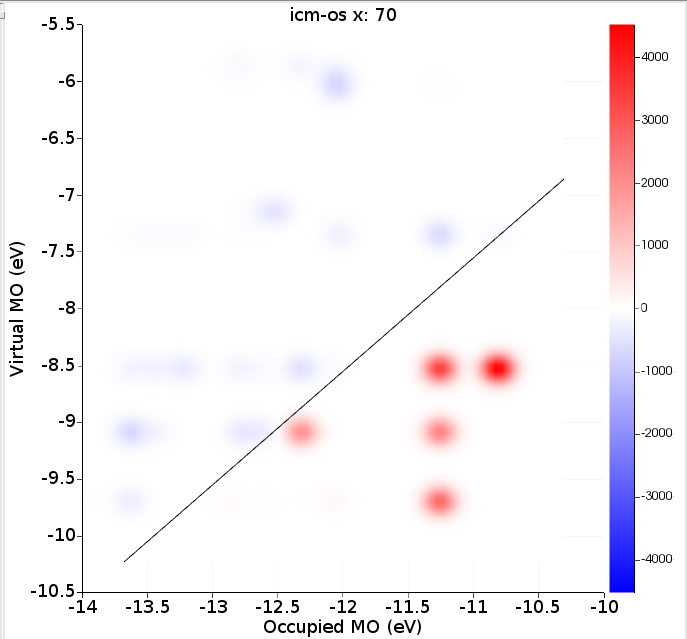
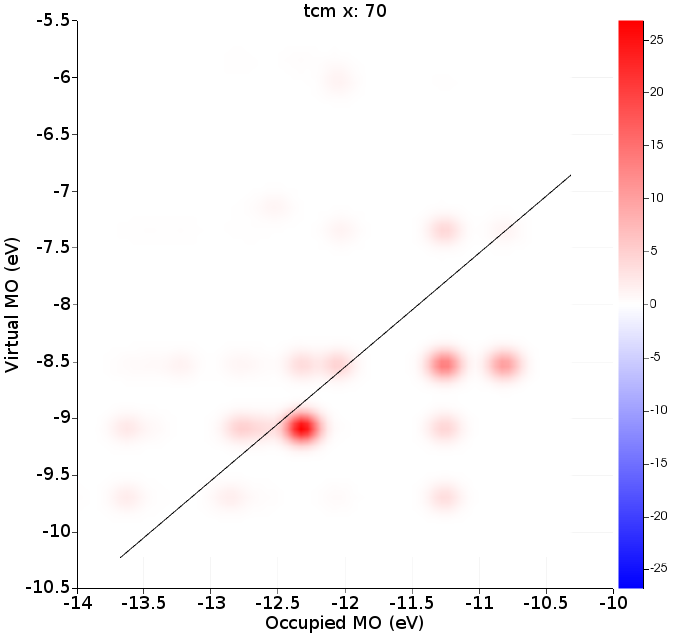
ICM-OS (Ref. 1) allows one to analyze and better understand the features of electronic transitions. It allows one to decompose a specific absorption peak in terms of electronic single orbital transitions labeled by the energy of the occupied (x-axis) and virtual (y-axis) orbitals involved. The diagonal line shows where the excitation energy matches a difference in occupied and virtual energies. In addition to the weight of each pair of orbitals in the oscillator strength, ICM-OS also accounts for the signs of the associated dipole contributions, which may result in constructive (in red) or destructive (in blue) interference among excited configurations. TCM is more focused on a description of the excited state in terms of electronic single orbital transitions (with only positive contributions) than being suited to rationalize the mechanisms which are behind absorption.

Open SCM → Output

Find the PolTDDFT analysis for the X component at frequency 3.45 eV.

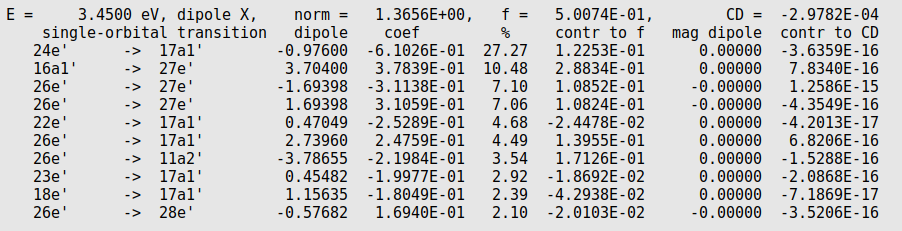
In the output one can find

• %: the relative character of a single orbital transition (SOT), like the TCM plot is showing,

• contr to f: how much this SOT character contributes to the oscillator strength, like the ICM-OS plot is showing.

To know the energy of an orbital it helps to open an AMSLevels window.

Open SCM → Levels

Hide the fragment stacks: View → Hide/Show all Fragments

Show the labels: View → Labels → Show

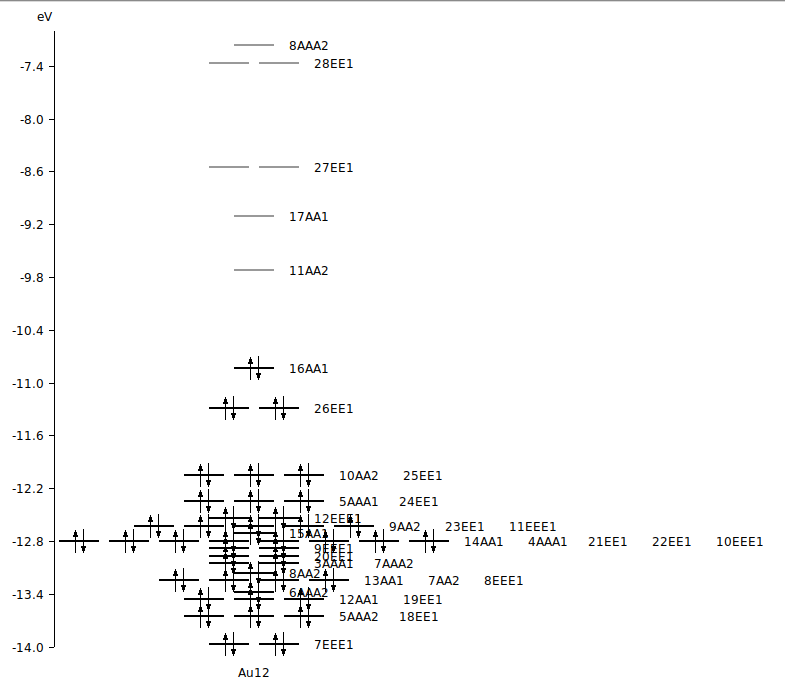
Note that irreps for D(3H) in ADF are sometimes written as AA1, AAA1, AA2 AAA2, EE1, and EEE1, they stand for A1’, A1’’, A2’, A2’’, E1’, and E1’’. So the SOT 24e' -> 17a1' is from the orbital 24EE1 to the orbital 17AA1

One can imagine that for a larger gold cluster the number of SOTs that may be important at a certain frequency may grow rapidly. In that case the TCM plot and ICM-OS plot are easier to understand.

1(1,2)

S. Theivendran, L. Chang, A. Mukherjee, L. Sementa, M. Stener, A. Fortunelli, and A. Dass, Principles of Optical Spectroscopy of Aromatic Alloy Nanomolecules: Au_36-x Ag_x (SPh-tBu)₂₄, Journal of Physical Chemistry C 122, 4524 (2018)

2(1,2)

L. Sementa, G. Barcaro, O. Baseggio, M. De Vetta, A. Dass, E. Aprà, M. Stener, and A. Fortunelli, Ligand-Enhanced Optical Response of Gold Nanomolecules and Its Fragment Projection Analysis: The Case of Au₃₀ (SR)₁₈, Journal of Physical Chemistry C 121, 10832 (2017)