GW-BSE: the singlet-triplet (S0-T1) gap of Benzene¶
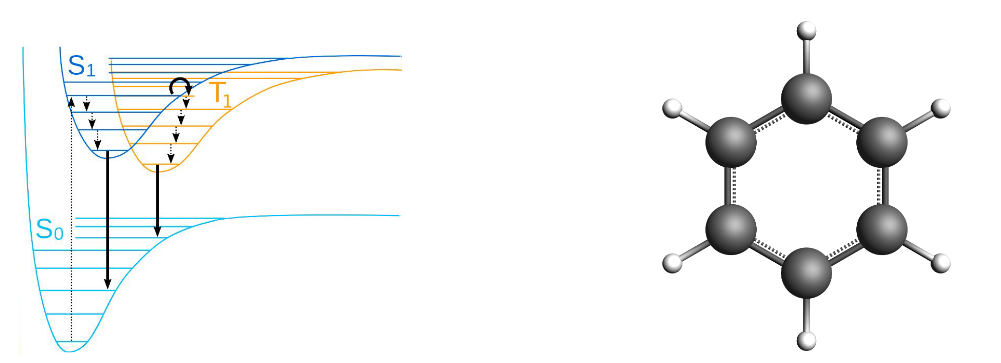
In a GW-Bethe-Salpeter Equation (GW-BSE) calculation a GW calculation is performed to calculate single-particle energies and the screened electron-electron interaction which are then used to calculate optical excitation energies.
The singlet-triplet gap of Benzene is defined here as the energy difference between the ground state energy and the lowest excited triplet state, \(\Delta E = E(T_{\mathrm{1}}) - E(S_{\mathrm{0}})\). Here vibrational effects and geometry relaxation are not taken into account. At the moment this is also not possible to take into account at the BSE level.
Using an all electron TZ2P basis set is typically sufficient for BSE calculations, where excitation energies are calculated. Remark: to obtain good quasi-particle energies one typically needs to use larger basis sets.
The cheapest method for BSE is G0W0-BSE, but then it is important to choose the right starting point. Recommended for G0W0-BSE is to use a hybrid functional with 40-50% Hartree-Fock exchange, and not, for example, PBE or LDA. Self-consistent methods improve the starting point dependence. For best precision and least starting point dependence qsGW-BSE is the recommended method, but this method has higher requirements on numerical settings than the other BSE methods. A useful alternative may be evGW-BSE, which is more starting point dependent than qsGW-BSE, but less than G0W0-BSE.
In AMS2023.102 a bug was fixed regarding GW. An incorrect Fermi energy was used, which also affected BSE.
Warning
The implemented GW algorithm is very sensitive to numerical noise and on the numerical (MBPT) settings. Using the same numerical settings, quasiparticle energies from partially self-consistent GW calculations performed on different hardware can differ by a few meV. See also the ADF manual on GW and ADF manual on MBPT settings.
Summary of results¶
Experimental singlet-triplet gap of benzene: 3.66 eV
The calculation time is an example for a typical compute node.
Method |
Starting point |
Singlet-triplet gap (eV) |
Calculation time (s) |
|---|---|---|---|
G0W0-BSE |
PBE |
3.23 |
45 |
G0W0-BSE |
PBE0 (40% HF exchange) |
3.58 |
50 |
evGW-BSE |
PBE |
3.45 |
104 |
evGW-BSE |
PBE0 (40% HF exchange) |
3.59 |
102 |
qsGW-BSE |
PBE |
3.71 |
135 |
qsGW-BSE |
PBE0 (40% HF exchange) |
3.71 |
118 |
G0W0-BSE¶
We start with G0W0-BSE, a method that is starting point dependent. Typically what works best in this case is to use a hybrid functional with around 40-50% Hartree-Fock exchange. Here we will use PBE0, where we manually change the amount of HF exchange to 40%, and we call this modified functional PBE0_40.
C 0.69542982 -1.20451978 0.00000000
C -0.69542982 -1.20451978 0.00000000
C 1.39085964 0.00000000 0.00000000
C -0.69542982 1.20451978 0.00000000
C 0.69542982 1.20451978 0.00000000
C -1.39085964 0.00000000 0.00000000
H 1.23647506 -2.14163763 0.00000000
H -1.23647506 -2.14163763 0.00000000
H 2.47295012 0.00000000 0.00000000
H -1.23647506 2.14163763 0.00000000
H 1.23647506 2.14163763 0.00000000
H -2.47295012 0.00000000 0.00000000
 panel
panel40 for the ‘HF exchange (for hybrids)’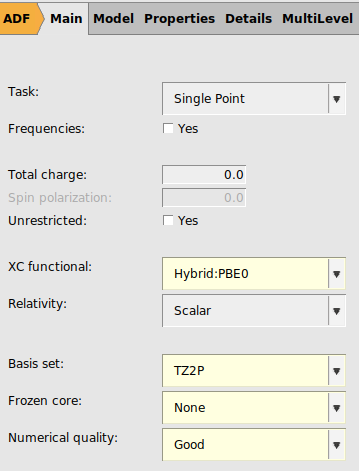
2 for the ‘Number of excitations`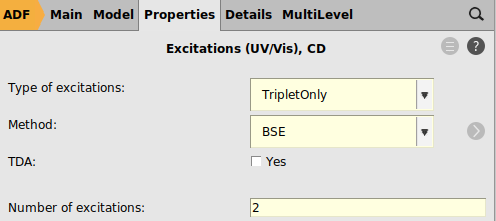
If the HOMO and/or LUMO of a molecule are/is degenerate, like in Benzene, we may need to calculate more than 1 for the number of excitations, even if we are interested only in the lowest energy. This is true especially if symmetry is used, like in this calculation. For this calculation 2 seems to be sufficient, otherwise try 4.
We are now ready to run the calculation.
benzene_g0w0_pbe0_40 using File → Save As…. → Output
→ Output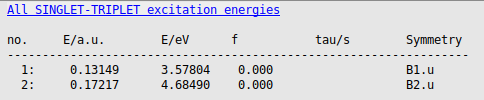
The calculated lowest triplet excited state energy with G0W0@PBE0_40-BSE is around 3.58 eV, close to the experimental number of 3.66 eV. If we would have used the G0W0@PBE-BSE, thus use PBE as starting point, this energy would be around 3.23 eV, thus the starting point matters a lot in G0W0-BSE.
evGW-BSE¶
To overcome partly the starting point dependence we now use evGW, in which the quasi particle energies are calculated self-consistently, but not the density. Like for G0W0-BSE, recommended for evGW-BSE is to use a hybrid functional with around 40-50% Hartree-Fock exchange as starting point. For educational purposes here we use a relatively poor starting point: PBE.
 panel
panel2 for the ‘Number of excitations`

We are now ready to run the calculation.
benzene_evGW_pbe using File → Save As…. → Output
→ OutputThe calculated lowest triplet excited state energy with evGW-BSE@PBE is around 3.45 eV, improving on G0W0@PBE-BSE, if it is compared to experiment. If we would have used the evGW@PBE0_40-BSE, this energy would be around 3.59 eV, close to the G0W0@PBE0_40-BSE value.
qsGW-BSE¶
To overcome the starting point dependence (almost completely) we now use qsGW, in which the quasi particle energies and density are calculated self-consistently.
 panel
panel2 for the ‘Number of excitations`
We are now ready to run the calculation.
benzene_qsGW_pbe using File → Save As…. → Output
→ Output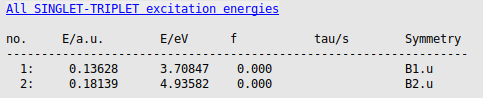
The calculated lowest triplet excited state energy with qsGW@PBE-BSE is around 3.71 eV, which is close to the experimental number of 3.66 eV. If we would have used qsGW-BSE with PBE0_40 as starting point, this energy would be the same, also 3.71 eV.