CD and CPL for spin-forbidden electronic transitions¶
Circularly polarized luminescence (CPL) dissymmetry factors and phosphorescence lifetimes are calculated for the spin-forbidden triplet emission of a platinahelicene complex, as is done in Ref. [1] on which this Tutorial is based. Spin-orbit coupling is included in the relativistic time-dependent density functional calculations. Emission from a triplet state to a singlet state is spin forbidden, however, due to spin-orbit coupling such transitions may occur.
For phosphorescence one needs to compute the geometry of the lowest excited triplet state (T1), see for example the Tutorial Vibrational progression of an OLED phosphorescent emitter. Here the T1 optimized structure of platinahelicene P-3 c will be taken from Ref. [1].
Pt 1.88557 -0.18819 -0.09184
N 0.53248 -1.39044 -0.93333
O -0.83139 4.50753 -0.36816
O 3.16072 1.14825 0.73682
O 3.42989 -1.63253 -0.16462
C 0.38349 1.05819 -0.12840
C 0.40946 2.43348 -0.07897
H 1.35956 2.94635 0.08566
C -0.78729 3.16948 -0.27172
C -2.06683 2.51788 -0.28913
C -3.26016 3.26301 -0.43357
H -3.19230 4.33714 -0.61567
C -4.48585 2.63006 -0.39893
H -5.40156 3.20093 -0.58304
C -4.59331 1.25914 -0.08686
C -5.87212 0.62486 -0.02698
H -6.75377 1.21811 -0.28983
C -6.00026 -0.68193 0.33815
H -6.98145 -1.16545 0.35914
C -4.85822 -1.41901 0.79804
C -5.01464 -2.70951 1.35136
H -6.00988 -3.16539 1.34100
C -3.94932 -3.37509 1.92985
H -4.09079 -4.36918 2.36459
C -2.69421 -2.74701 1.99285
H -1.85786 -3.23921 2.49787
C -2.51273 -1.49672 1.42702
H -1.53683 -1.01466 1.51801
C -3.56458 -0.81800 0.77077
C -3.40060 0.49872 0.16186
C -2.14212 1.09766 -0.13877
C -0.89804 0.39244 -0.39652
C -0.75395 -0.88046 -1.01165
C -1.74669 -1.62254 -1.69388
H -2.74468 -1.19458 -1.80010
C -1.44205 -2.85403 -2.23570
H -2.20476 -3.42159 -2.77596
C -0.13832 -3.36681 -2.09214
H 0.14108 -4.34342 -2.49279
C 0.81493 -2.59285 -1.44363
H 1.85025 -2.92292 -1.32054
C 0.36036 5.25424 -0.31870
H 0.07055 6.30544 -0.46034
H 1.05601 4.95538 -1.12332
H 0.86335 5.14614 0.65906
C 5.09120 2.13040 1.60594
H 4.57183 2.42528 2.53454
H 5.02604 2.98776 0.91312
H 6.14843 1.92825 1.83129
C 4.39181 0.94494 0.99921
C 5.11332 -0.23796 0.77878
H 6.16563 -0.22805 1.06805
C 4.61920 -1.43558 0.22324
C 5.55256 -2.60481 0.05850
H 5.14292 -3.47731 0.59695
H 6.56771 -2.39569 0.42671
H 5.60487 -2.88044 -1.00966
Relatively cheap settings¶
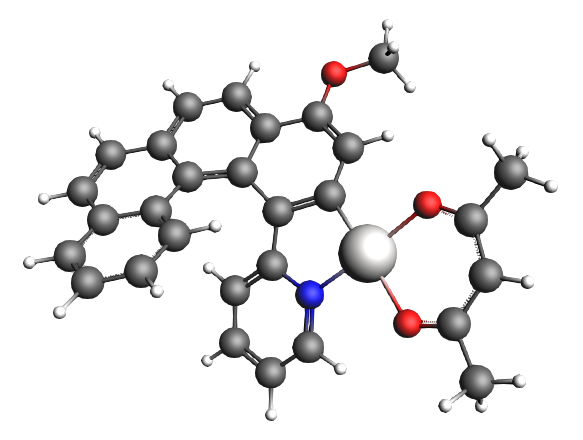
As the settings that are used in the paper will lead to a long calculation, first a gas phase PBE calculation will be performed with a DZ frozen core basis set, using spin-orbit coupled TD-DFT with TDA to calculate rotatory strengths. This is a relatively cheap calculation and thus does not take so long.
 panel
panel3 for the ‘Number of excitations`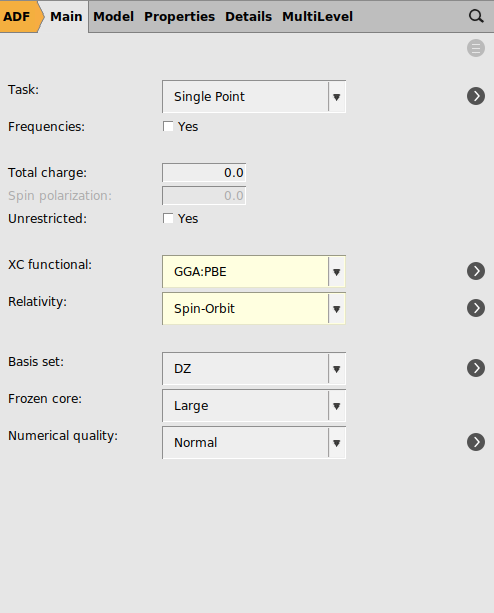
We are now ready to run the calculation.
P-3c_pbe_dz using File → Save As…. → Output
→ Output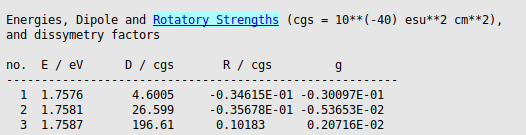
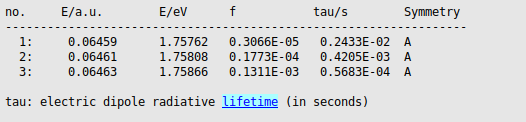
The calculated results are quite sensitive to small numerical changes, since we are looking at a small effect.
The averaged dissymmetry factor for the emission can be computed using rotatory and dipole strengths that are Boltzmann-averaged over the triplet components:
In this case the energy of the triplet components are very close (1.75762, 1.75808, and 1.75866 eV), thus we will use
Also the averaged radiative lifetime can be computed using lifetimes that are Boltzmann-averaged over the triplet components:
In this case we will use again that the energy of the triplet components are very close, thus we will use
Note that here no refractive index of a solvent is included, as this is a gas phase calculation.
Tip
Insert the values into the below Python script and use it to calculate the values:
#!/usr/bin/env amspython
import numpy as np
from scm.plams import Units
def get_values():
E_eV = np.array([1.7576, 1.7581, 1.7587])
D = np.array([4.6005, 26.599, 196.61])
R = np.array([-0.34615e-1, -0.35678e-1, 0.10183])
tau = np.array([0.2433e-2, 0.4205e-3, 0.5683e-4])
refractive_index = 1
return E_eV, R, D, tau, refractive_index
def main():
E_eV, R, D, tau, refractive_index = get_values()
use_boltzmann_weights = False
if use_boltzmann_weights:
weights = calc_boltzmann_weights(E_eV, T=298)
else:
weights = np.ones(np.shape(E_eV))
g = 4 * np.dot(R, weights) / np.dot(D, weights)
print(f"g_lum_av: {g:.3e}")
tau_av = 1.0 / refractive_index**2 * np.sum(weights) / np.dot(1.0 / tau, weights)
print(f"tau_av: {tau_av:.3e} s")
def calc_boltzmann_weights(E_eV, T=298):
k_B = Units.constants["k_B"] * Units.convert(1, "J", "eV") # eV/K
boltzmann_weights = np.exp(-(E_eV - np.min(E_eV)) / (k_B * T))
return boltzmann_weights
if __name__ == "__main__":
main()
Settings as in the paper¶
Next we will try to use the same settings as are used in Ref. [1]: spin-orbit coupled TD-DFT with TDA to calculate rotatory strengths, the hybrid PBE0 XC functional, full XC kernel, a TZ2P basis all electron basis set on Pt, DZ all electron on H, and DZP all electron on all other elements, dichloromethane as COSMO solvent, and numerical quality good. This is a much more demanding calculation than with the previous settings.
 panel
panel3 for the ‘Number of excitations’

ZORA/TZ2P/Pt for PtZORA/DZ/H for H
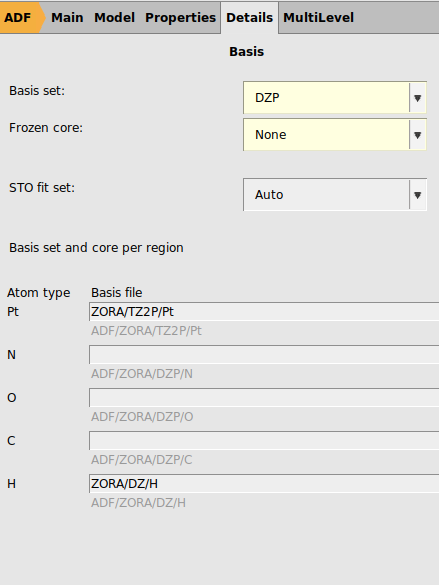
We are now ready to run the calculation. As this may take several hours on a cluster, and maybe even longer on a desktop, one could also skip the calculation, and directly look at the results below.
P-3c_pbe0 using File → Save As….
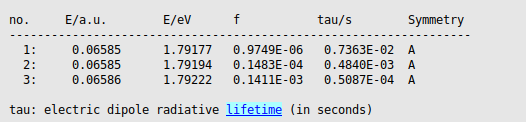
The averaged dissymmetry factor for the emission can be computed using rotatory and dipole strengths that are Boltzmann-averaged over the triplet components. In this case the energy of the triplet components are very close (1.79177, 1.79194, and 1.79222 eV), thus we will use
Also the averaged radiative lifetime is calculated without using Boltzmann factors as
where \(n=1.42\) is the refractive index of the dichloromethane solvent used in the measurements. For comparison, experimental data reported in Ref. [1] for P-3 c are 1.93 eV for the transition energy, a phosphorescence lifetime of 21 \(\mu s\), and a \(g_{lum}\) of 3 10-3, see also the discussion of the results in the paper.