TDDFT Study of 3 different Dihydroxyanthraquinones¶

Scientific Questions¶

Q1 When looking at 3 different Dihydroxyanthraquinones, does the position of the hydroxyl groups influence the charge transfer occurring when these molecules are exposed to UVvis light?

Q2 Which vertical electron transfers are responsible for the absorption in the blue region of the UVvis spectra?

Model Questions¶

AMS offers 4 options of TDDFT, which one is best suited for the problem at hand?

TDDFT

• the standard method for excitations in ADF;

• works for LDA, GGA, hybrids, range-separated hybrids;

• it can do an excited state geometry optimization for LDA, GGA, hybrids, and range separated hybrids (with XCFUN).

TDDFTB

• fast standard method for excitations in DFTB;

• excited state geometry optimization is possible.

TDDFT+TB

• excitation method using DFT orbitals from ADF, kernel from DFTB;

• only for LDA+GGA, especially useful if many excitations are required, then it’s much faster than standard TDDFT;

• since AMS2023 excited state geometry optimization is possible.

sTDDFT

• excitation method using DFT orbitals from ADF, kernel from DFTB;

• only for hybrids (and with special parameters for range separated hybrids);

• especially useful if many excitations are required, then it’s much faster than standard TDDFT for hybrids;

• excited state geometry optimization is not possible.

Prerequisites¶

You should be comfortable drawing a structure, setting up a calculation when given hints, running it, and retrieving results. If not, you can refresh your GUI skills here.

Overview¶

We will first have to validate our method as we have to show our peers that our choices indeed can deliver credible answers. TDDFT is mentioned very often in the literature and the description in the ADF manual refers to it as a standard method. This makes it a good candidate for a first attempt.

We want to see how good ADF can predict the absorption maxima in the UVvis spectra of 1,4-, 1,5- and 1,8- Dihydroxyanthraquinone (DHAQ) For this we’ll use experimental spectra reported by Zhang et al [1]. These compounds work as photo-initiating systems and show absorption maxima in the blue light wavelength range, which makes them potential candidates to work under the irradiation of blue LED bulbs.

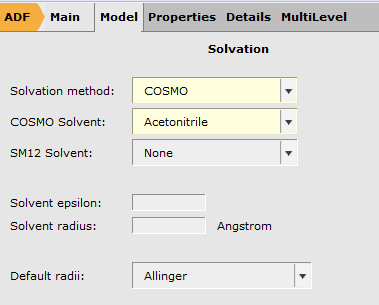
The spectra have been recorded in Acetonitrile which means we have to think about why/if this is important for our calculations – we may have to include solvent effects in our calculations as well. We will talk about this in detail below. We also will only study the absorption in the violet/blue range of the UVvis spectrum, i.e. 380 -485 nm.

It is always a good idea to make a short note of what information we have. We know about the structures, their symmetry and experimental UVvis results.

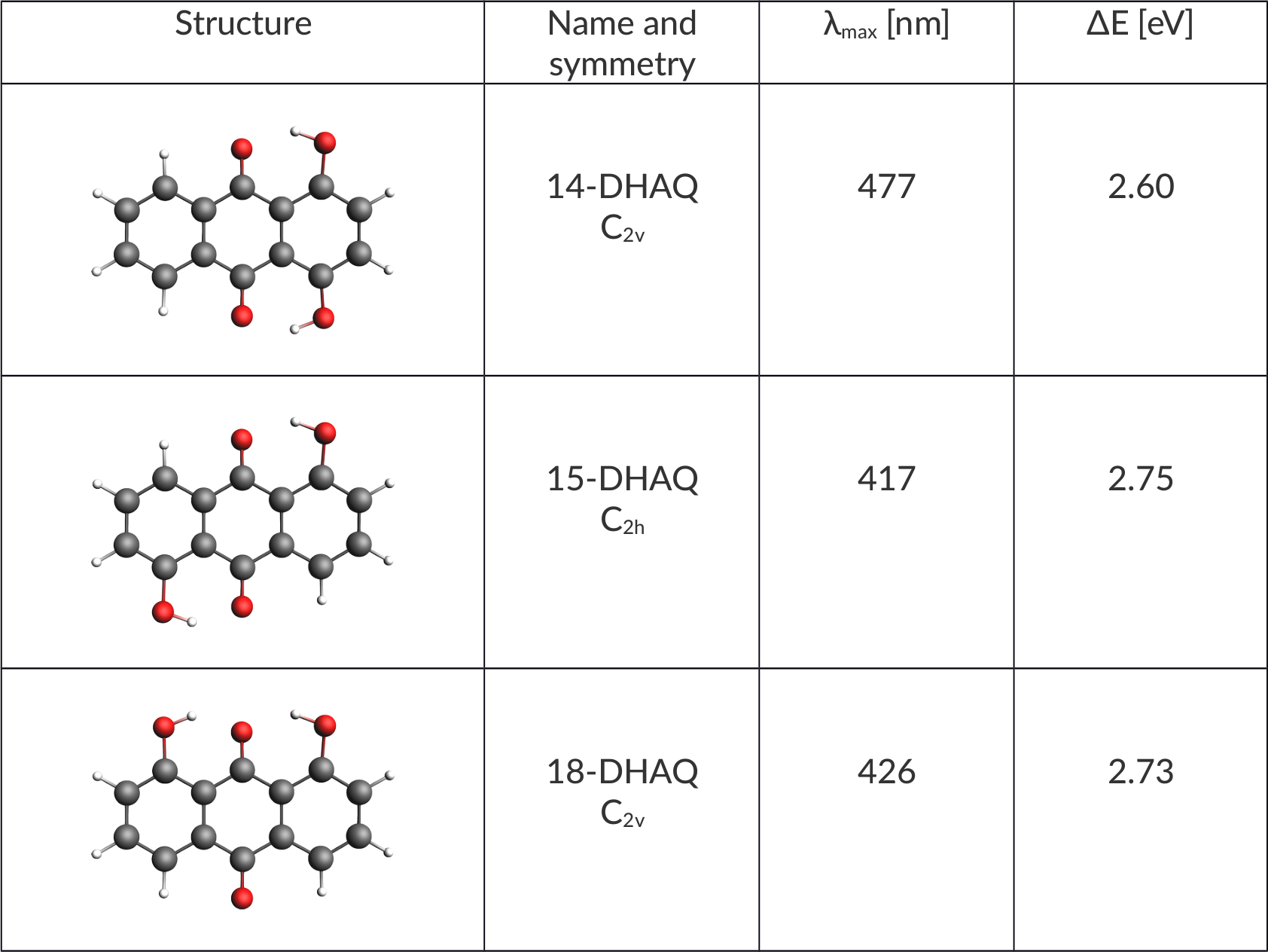
Symmetry can help us to understand which electron transitions are allowed, as transitions between states of the same parity are forbidden. (Laporte Rule). So, by knowing beforehand what the symmetry of a molecule is we can look at the character table of a point group and work it out.

A proper comparison with experimental spectra would require the inclusion of vibronic effects and a very accurate description of the solvent effects. TDDFT does not cater for vibronic effects and the solvent model we are going to use is an implicit one and describes solvent effects via a dielectric continuum (see COSMO). Also, the quality of the obtained results is profoundly functional-dependent and there is no systematic way to check for improvement. This means we often have to find for each compound family the optimal functional.

Our DHAQ structures will most likely show n → π * and π → π * transitions as we have an aromatic system with four oxygen atoms. There also will be intramolecular charge-transfer absorption as we have groups with both electron donating and -accepting properties.

Solvents do affect exited species, and peaks resulting from n → π * transitions are shifted to shorter wavelengths (blue/hypsochromic shift). With increasing solvent polarity increased solvation of the lone pair occurs, which lowers the energy of the n orbital. Often (not always), a red/bathochromic shift is seen for π → π * due to attractive polarization forces which lower the energy levels of both the excited and non-excited states.

0. What functional, What basis set?¶

A good starting point is to follow the best-practice advice in SCM’s FAQ section. Further aid can be found in the many overview articles published on TDDFT, e.g.

D. Jacquemin, V. Wathelet, E.A. Perpete, and C. Adamo, Extensive TD-DFT Benchmark: Singlet-Excited States of Organic Molecules, J. Chem. Theory Comput. 2009, 5, 2420–2435

D. Jacquemin, E.A. Perpete, G.E. Scuseria, I.Ciofini, and C. Adamo TD-DFT Performance for the Visible Absorption Spectra of Organic Dyes: Conventional versus Long-Range Hybrids, J. Chem. Theory Comput. 2008, 4, 123-135

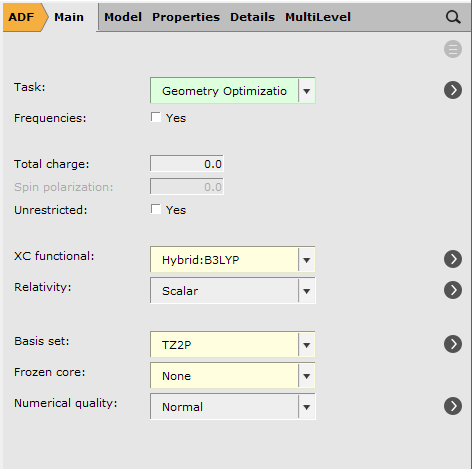
1. Geometry Optimization¶

To optimize all three DHAQ isomers use the following workflow. Make sure to choose sensible names for your files such as 14_DHAQ_opt.ams and 14_DHAQ_f.ams so you easily recognize the structure and the sort of computation you did.

Build each molecule as shown in the table above and make sure the OH do form intramolecular hydrogen bonds with the C=O group. (It is convenient to start from the anthracene geometry, which you can import from the molecule database by clicking the magnifying glass on the top right and typing “anthracene”.)

Symmetrize the molecule by clicking on .

Do not worry if your molecule does not quite have the correct symmetry yet. The geometry optimization will take care of making it symmetric enough, so that it will become perfectly symmetric when we later run the symmetrizer again.

To setup the geometry optimization:

Once the calculation has finished, you can proceed to the TDDFT calculations. Select “Yes, new job” when prompted to update coordinates after the geometry optimization calculation. Repeat this for all of your 3 DHAQ structures.

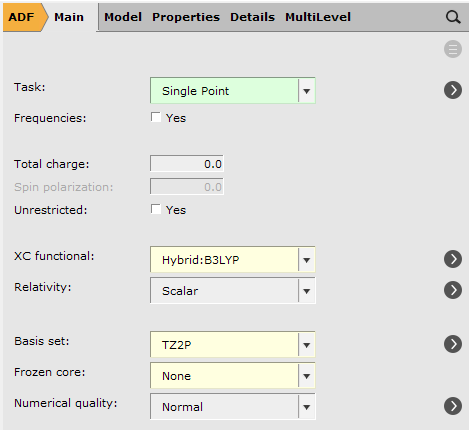
2. TDDFT Calculations¶

To run a TDDFT calculation, make sure you are using the optimized geometries from the previous step, which should already be the case if you selected “Yes, new job” at the previous step. Note that the following step must also include the solvation options previously selected for the geometry optimization steps.

In the Main tab choose

Task → Single Point

Symmetrize the molecule by clicking on .

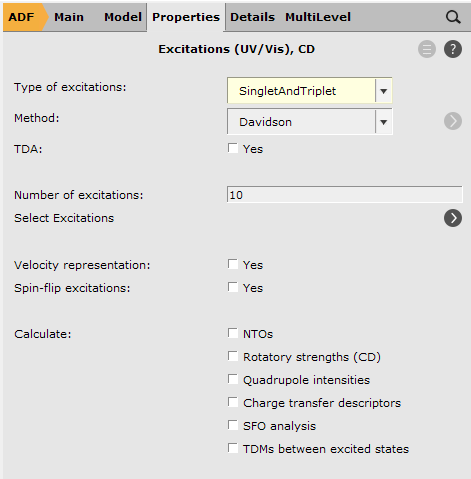
3. Analyzing TDDFT Calculations¶

We will discuss this section using the data of 14-DHAQ.

You now can explore your spectrum.

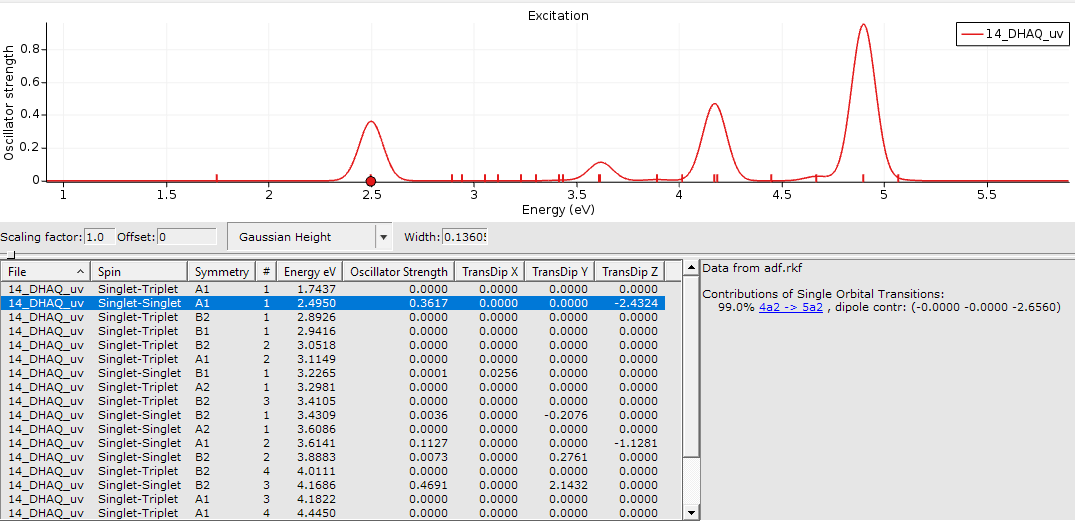
You can investigate peaks, see the symmetry of your transition, the absorption energy in eV and which orbitals are contributing. The peak of interest is the one at 2.495 eV. which we will refer to as 2.50 eV in the following.

We plan to revisit the actual orbital transition details a bit later. For now, we want to compare our calculations with the experimental data and tabulate the results.

As you can see we got excellent results. Before we move on and discuss the nature of these transitions in detail we want to divert and look into computational effort. You will agree, it did take some time to obtain our results and if we were only interested in these 3 structures it may be ok. However, often we may be confronted with a larger set of structures and some pressure to provide answers fast - and then speed can matter. Thus, we would like the option of a faster method but still have a good accuracy.

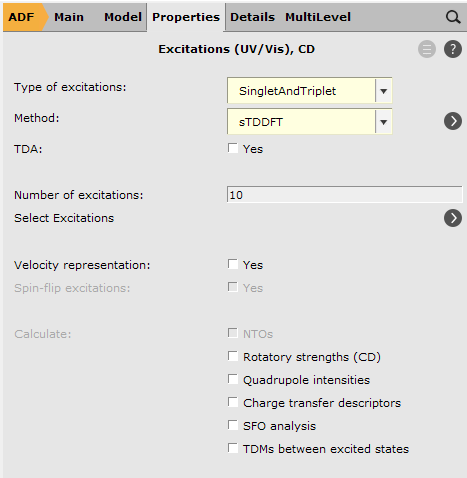
4. Faster TDDFT variant: sTDDFT¶

As mentioned in the introduction, the Amsterdam Modeling Suite has several methods that can be used to speed up the calculation of vertical excitation energies. Among others these are

• sTDDFT by Bannwarth and Grimme[2]

• TDDFT+TB = Uses the molecular orbitals from a DFT ground state calculation as input to an excited state calculation with TDDFTB coupling matrices.

• TDDFTB = Time dependent density functional tight-binding.

The acronym sTDDFT stems from “simplified time-dependent density functional theory” and the method allows fast computation of UVvis or circular dichroism (CD) spectra of molecules with 500-1000 atoms.

The method approximates the integrals needed for the exited states calculation and thus needs some parametrization.

Let us set up the calculations for our 3 DHAQ:

You can see the results are excellent and we saved a lot of time. How much time the calculation took, can be found in the output file of the calculation.

To show the timings, eg:

Total cpu time:         55.24
Total system time:       3.07
Total elapsed time:     58.83

The timing shows how much time (in seconds) was spent in the ADF code (CPU) and in the kernel (System), and how long did it take for the calculation to complete (Elapsed). You can compare the timing with the TDDFT calculation we ran earlier:

Total cpu time:       1675.52
Total system time:      32.81
Total elapsed time:   1722.08

This means on this particular hardware sTDDFT is 30 times faster than the corresponding TDDFT calculation.

5. Analyzing the Orbitals¶

When we study UVvis absorption properties we want to know which electrons are getting excited and from which occupied orbital they move into which virtual one.

For example, the calculated spectrum of 14-DHAQ was accompanied by some output describing the orbitals involved.

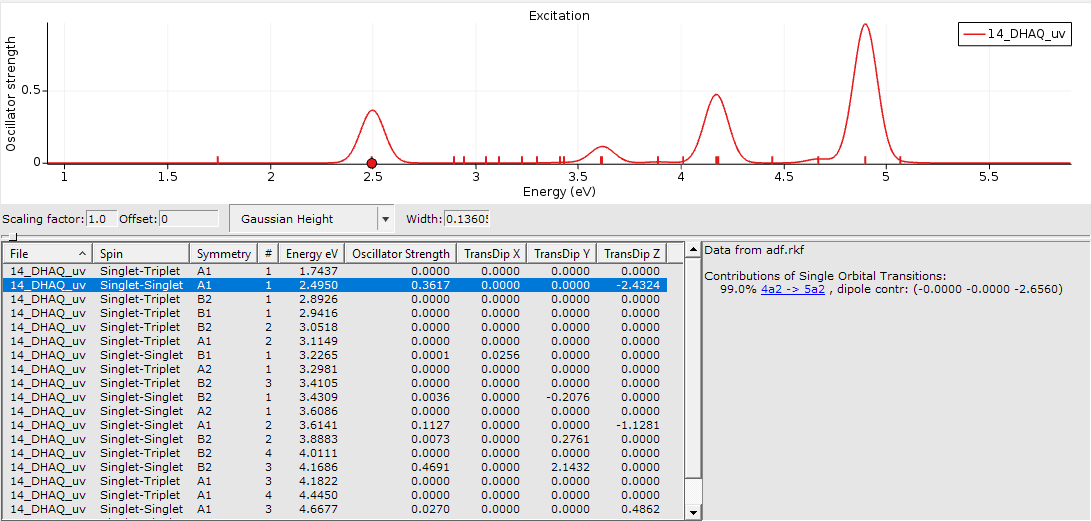
This one is very simple as only one occupied and one virtual molecular orbital (MO) are involved. For 99% the transition from MO 4a2 to MO 5a2 is associated with an excited state and our peak at 2.50 eV.

One of the occupied orbital with red and blue lobes and one of the virtual ones with turquoise and ochre lobes.

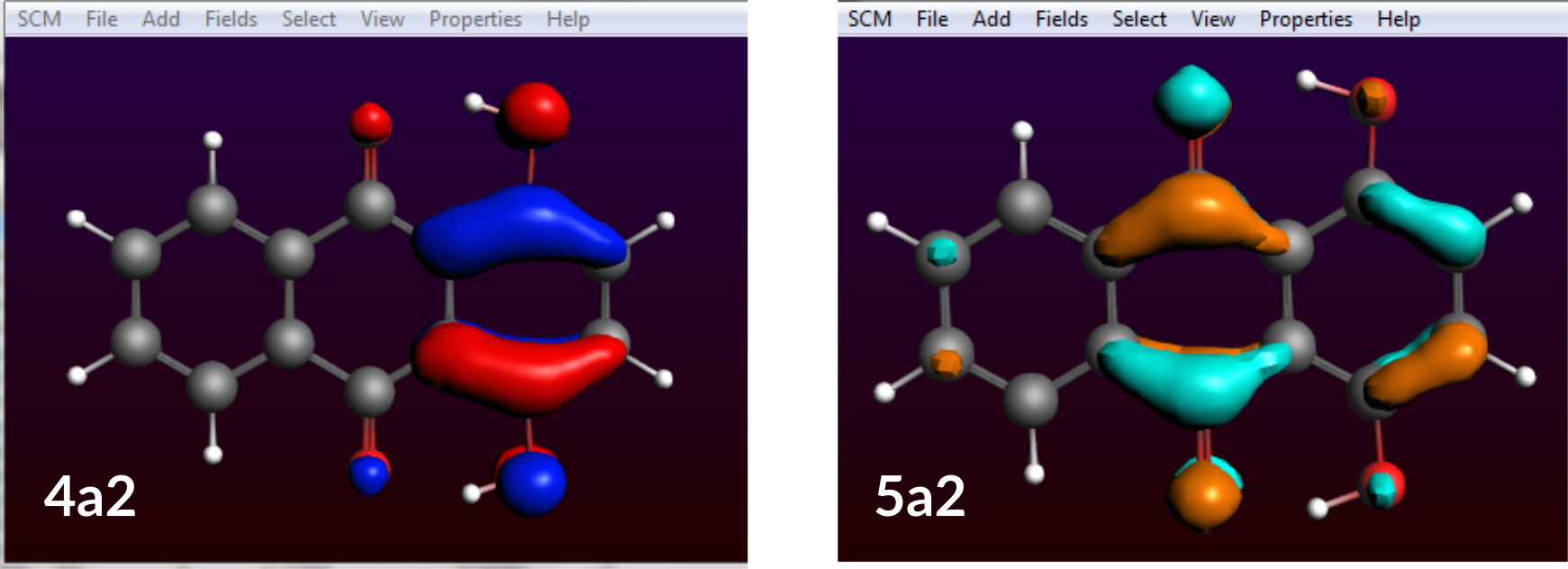
Now we need to find out what these MOs are:

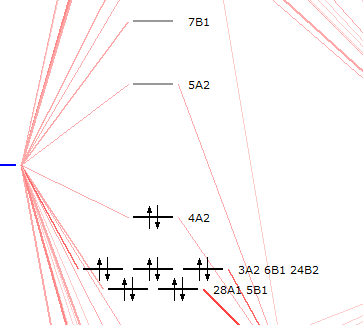
You will see 4A2 is the HOMO and 5A2 is the LUMO. Thus, you know now, that the peak at 2.50 eV is the HOMO-LUMO transfer.

6. Analyzing the NTOs¶

More often you will see in your outputs a list of MOs that contribute equally to an exited state. By transforming all of these MOs (see [3]) to a Natural Transition Orbital (NTO) we can simplify the qualitative description of an electronic transition.

As we are using B3LYP, we require the Tamm-Dancoff Approximation (TDA) before we can do this. TDA has its use for triplet excitations that often lead to instability in the wavefunction and result in imaginary TDDFT triplet excitation energies.

When your calculations are finished

You will get occupied and virtual NTO in one picture but you can look at them individually by un/checking the boxes next to Isosurface: With Phase.

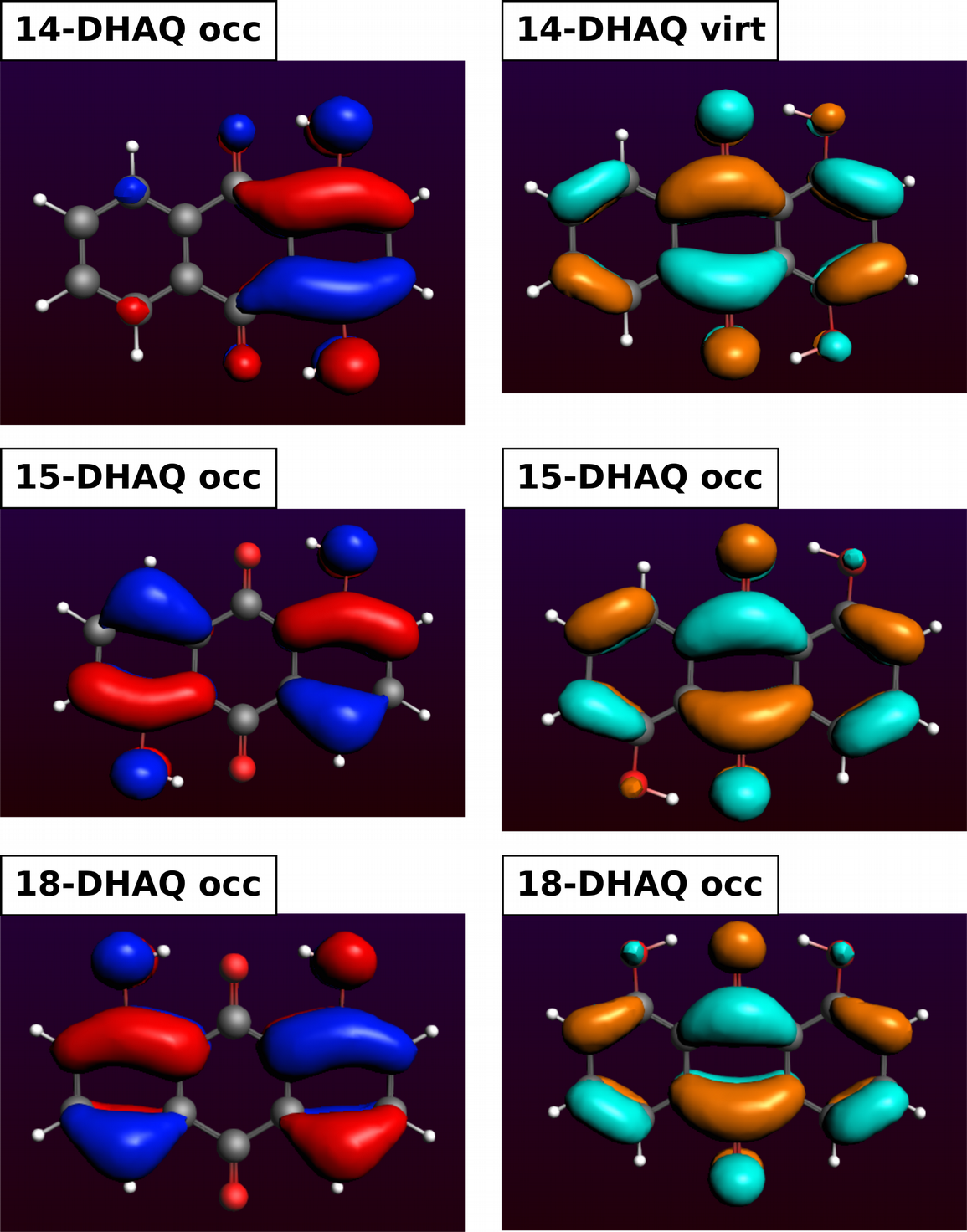
We can see that the lone pairs of the OH oxygen atoms are involved in all DHAQs. In 14-DHAQ the charge is mainly located in the ring carrying both OH groups which is a different behavior. Then we can see for all DHAQs, that the charge transfers to other parts in the molecule and moves to the antibonding C=O orbital, i.e. π*(C=O) but also to some of the π*(C=C).

Thus, can we answer our initial scientific questions?

Q1 When looking at 3 different Dihydroxyanthraquinones, does the position of the hydroxyl groups influences the charge transfer occurring when these molecules are exposed to UVvis light?

A1 Yes, the positions of the OH groups do influence where the charge is located in the ground state. In case of 14-DHAQ it is located mainly at the 6-ring with the two OH groups.

Q2 Which vertical electron transfers are responsible for the absorption in the blue region of the UVvis spectra?

A2 It’s the HOMO-LUMO transfers and lone pairs of the hydroxyl oxygen atoms are involved and some close-by π(C=C), and as acceptors π*(C=O) but also to π*(C=C) Mos.

7. Localized Analysis of Canonical Molecular Orbitals (CMO) with NBO6¶

Natural Bond Orbitals (http://nbo6.chem.wisc.edu/) can aid to provide a direct link to familiar valency and bonding concepts, similar to what we used from Lewis Structures.

Here in particular, we are interested in the CMO analysis, which allows us to tabulate the leading NBO contributions (bonding, nonbonding, or antibonding) to each canonical MO. Let’s try it and discuss it as we go along.

Next for NBO we need:

We had to disable the use of symmetry earlier, as it is not supported by the NBO program. We do require the Fock matrix to be written out because we need it for our CMO analysis. This is a non-standard feature that can be requested directly in the run script.

# ============
# NBO Analysis
# ============

"$AMSBIN/adfnbo" <<eor
write
fock
spherical
eor

"$AMSBIN/gennbo6" FILE47

"$AMSBIN/adfnbo" <<eor
spherical
fock
read
eor

$GENNBO NATOMS=  26 NBAS= 556 BOHR BODM $END
$NBO BNDIDX NBONLMO=W AONBO=W AONLMO=W NLMOMO=W STERIC FILE=adfnbo DIST $END
$COORD
****** (NO TITLE) ***

$GENNBO NATOMS=  26 NBAS= 556 BOHR BODM $END
$NBO CMO FILE=adfnbo $END
$COORD
****** (NO TITLE) ***

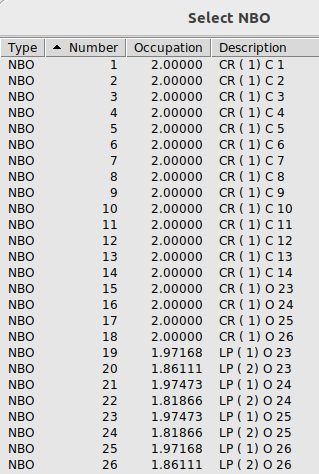
Once the calculation is finished do open cmo_output and scroll to “CMO: NBO Analysis of Canonical Molecular Orbitals”. Find MO 62 (occ) which is your HOMO. We find:

MO  62 (occ): orbital energy =   -0.23064 a.u.
             -0.498*[ 52]: BD ( 2) C10- C14
              0.498*[ 46]: BD ( 2) C 8- C 9
             -0.369*[ 24]: LP ( 2) O25(lp)
              0.369*[ 22]: LP ( 2) O24(lp)
             -0.308*[ 92]: BD*( 2) C12- C13*

Note that the numbers of the NBOs and ordering of the contributions may be slightly different. This can happen, for example, because of (near) degeneracies, however, the overall picture should be the same.

We find in square brackets [ ] the number of the NBO and BD stands for bond, CR for core, LP for lonepair and RY for Rydberg. BD* stands for anti-bonding and you may wonder now how the HOMO can be anti-bonding. NBO number [92] is not the same as a virtual MO. It just means some non-Lewis BD* character is weakly mixed in here. You will find the opposite for our LUMO: some Lewis-type BD [34] and [28] is mixing in here:

MO  63 (vir): orbital energy =   -0.11953 a.u.
             -0.472*[ 90]: BD*( 2) C11- O23*
              0.472*[ 80]: BD*( 2) C 7- O26*
              0.366*[ 92]: BD*( 2) C12- C13*
             -0.304*[ 74]: BD*( 2) C 4- C 6*
              0.264*[ 88]: BD*( 2) C10- C14*
             -0.264*[ 82]: BD*( 2) C 8- C 9*
              0.235*[ 34]: BD ( 2) C 3- C 5
             -0.235*[ 28]: BD ( 2) C 1- C 2

Next we want to visualize this NBOs in the AMSView:

For the HOMO we find

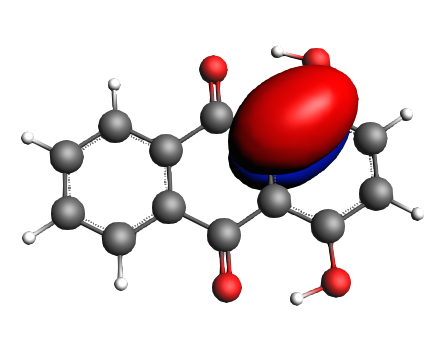
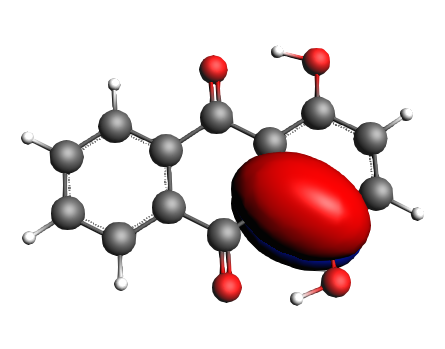
left: NBO 52 π (C=C), 25%; middle: NBO 46 π (C=C), 25%; right: NBO 24 LP Oxygen, 14%;

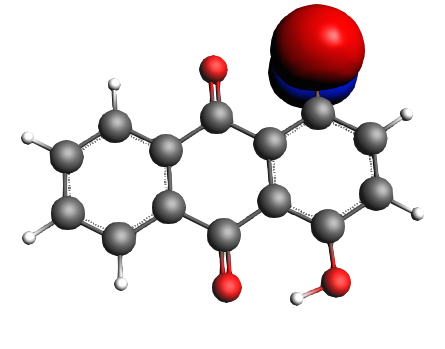
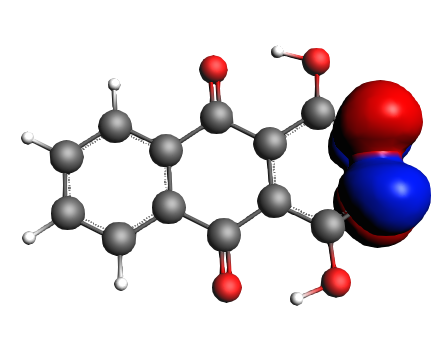
left: NBO 22 LP Oxygen, 14%; middle: NBO 92 π* (C=C), non-Lewis mixing in, 9%;

For the LUMO we find

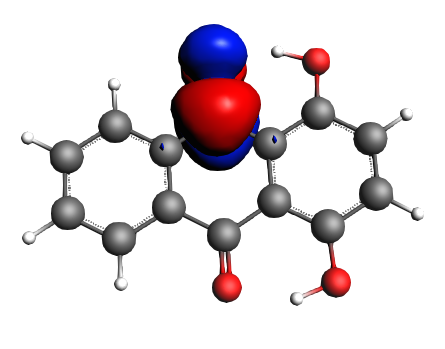
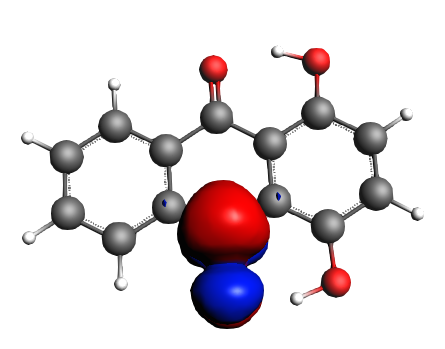
left: NBO 90 π* (C=O), 22%; middle: NBO 80 π* (C=O), 22%; right: NBO 92 π* (C=C), 13%;

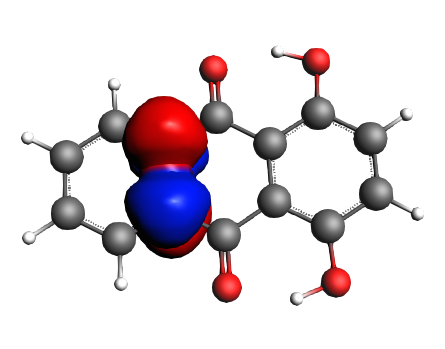
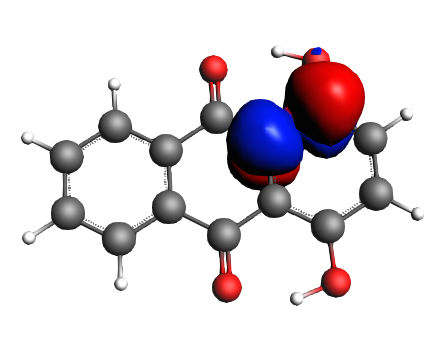
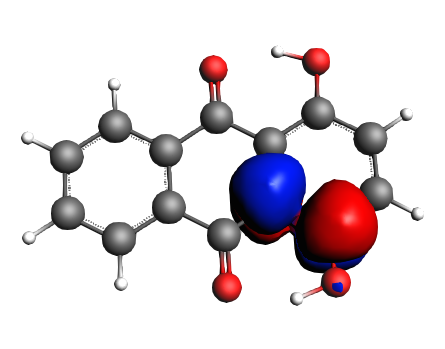
left: NBO 74 π* (C=C), 9%; middle: NBO 88 π* (C=C), 7%; right: NBO 82 π* (C=C), 7%;

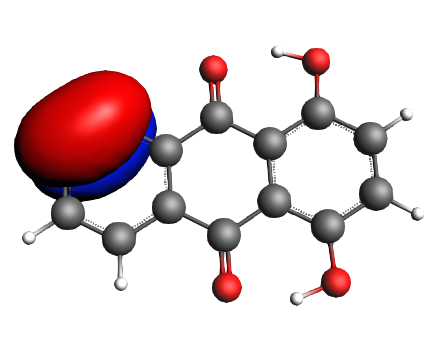
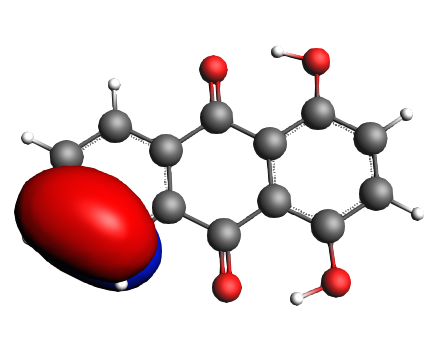
left: NBO 34 π (C=C), Lewis mixing in, 6%; middle: NBO 28 π (C=C), Lewis mixing in, 6%;

Now we can state the charge transfers from 50% of the π orbitals of the C=C bonds adjacent to the two OH groups and from 28% of the lone pairs of the two hydroxyl towards 48% of the π* orbitals of the C=O bonds and the rest of it settles in π* orbitals of C=C bonds, but never reaches quite as far as the most distant C=C bond of the furthest aromatic ring with respect to the di-hydroxyl moiety.

References

[1] J. Zhang, J. Lalevée, J. Zhao, B. Graff, M. H. Stenzel and P. Xiao Dihydroxyanthraquinone derivatives: natural dyes as blue-light-sensitive versatile photoinitiators of photopolymerization, Polym. Chem. 7, 7316 (2016).

[2] C. Bannwarth and S. Grimme, A simplified time-dependent density functional theory approach for electronic ultraviolet and circular dichroism spectra of very large molecules, Computational and Theoretical Chemistry, 1040–1041 (2014) 45-53 .

[3] R.L. Martin, Natural transition orbitals, J. Chem. Phys. 118 (2003) 4775-7 .