Electronic Transport¶
- Electronic transport in a carbon nanotube
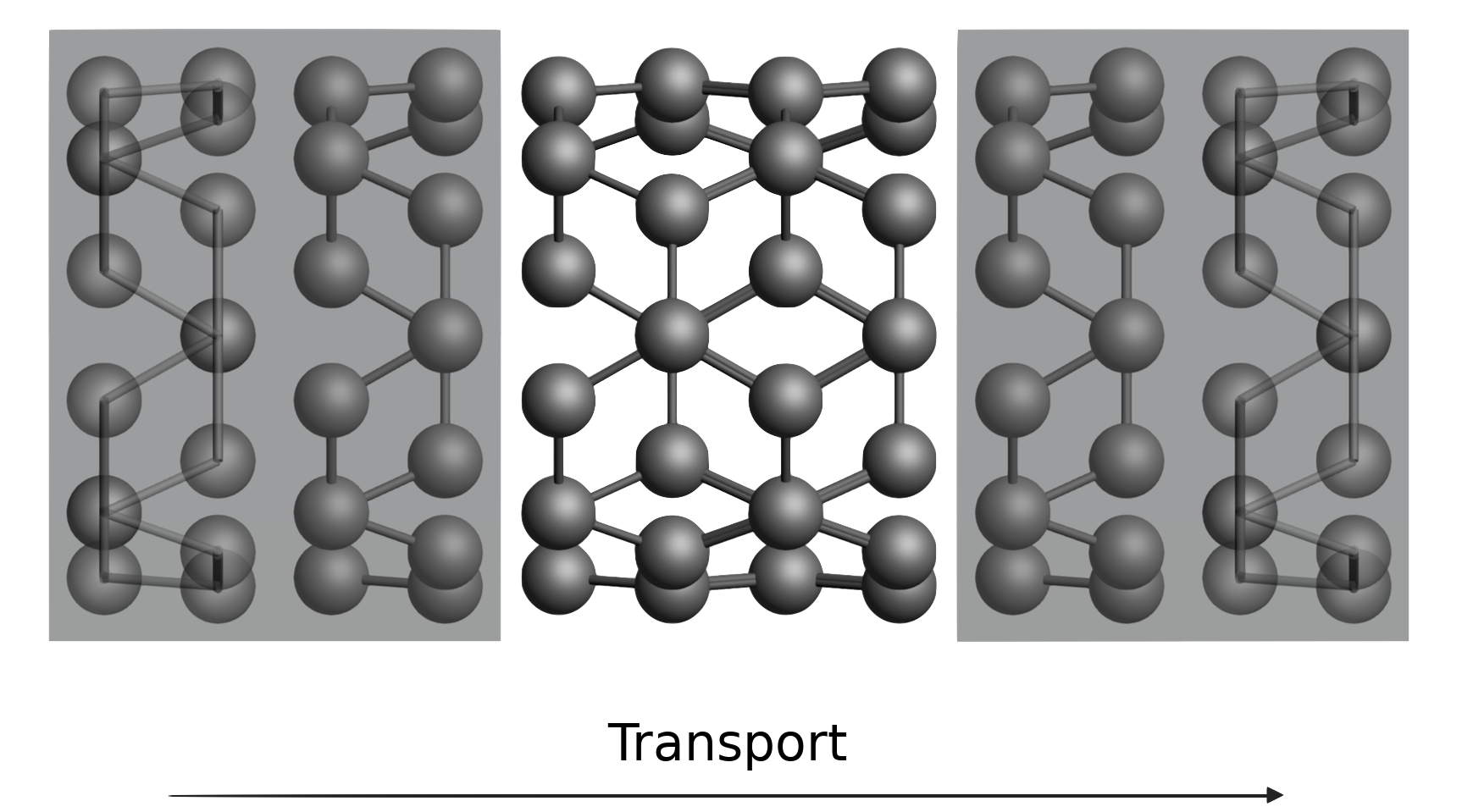
- Electronic transport in a 1D gold chain
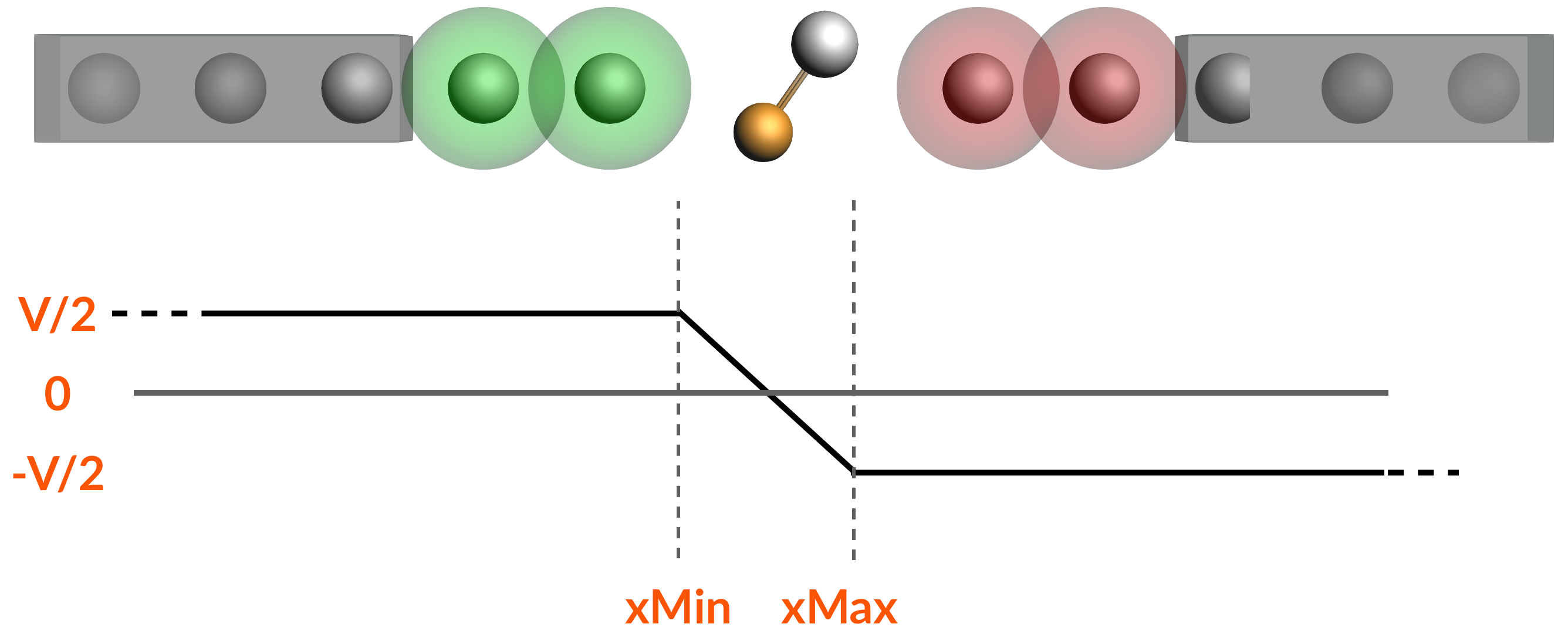
- Gate and Bias potentials
- Spin transport in Chromium wire
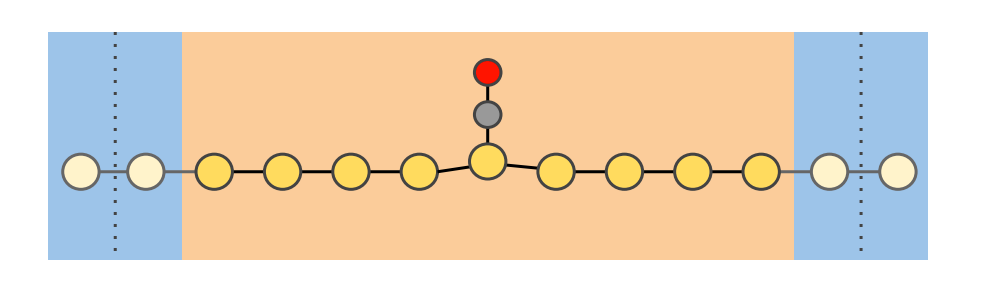
- NEGF: Create a Molecular Junction
- Electron and hole mobilities in organic electronics: charge transfer integrals
- Band Structure and Effective Mass Tensors of Phosphorene
Electronic transport in a carbon nanotube
Keywords: BAND, DFTB, organic electronics, NEGF (Non-Equilibrium Green’s Function), lead, transmission function, current
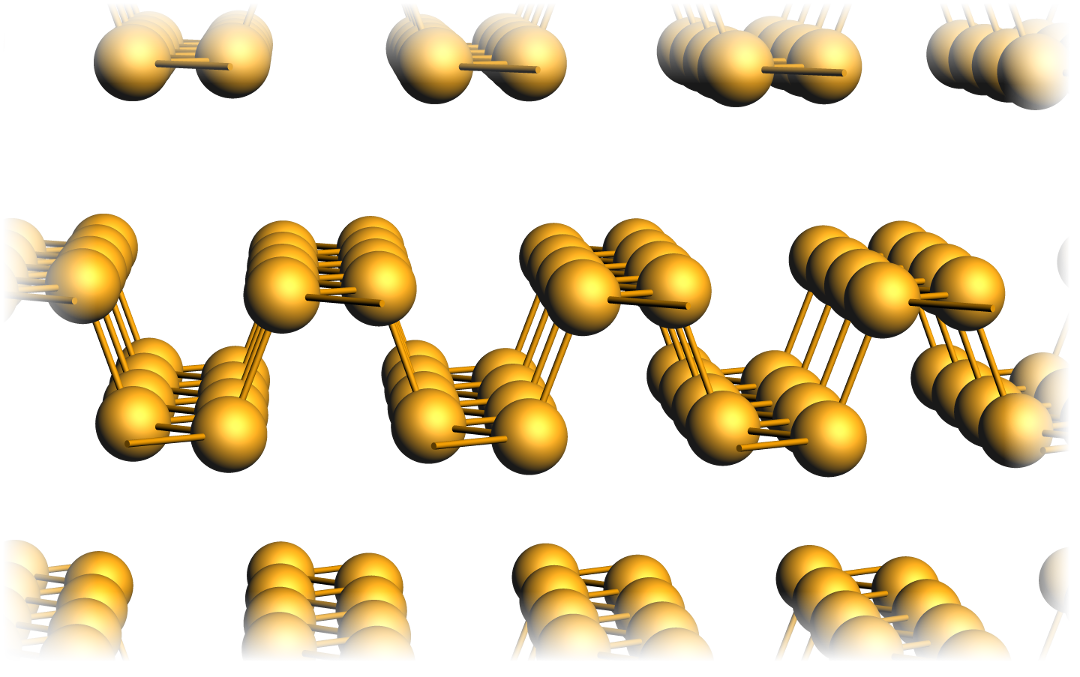
Electronic transport in a 1D gold chain
Keywords: BAND, DFTB, NEGF (Non-Equilibrium Green’s Function), metal wire, lead, transmission function, current
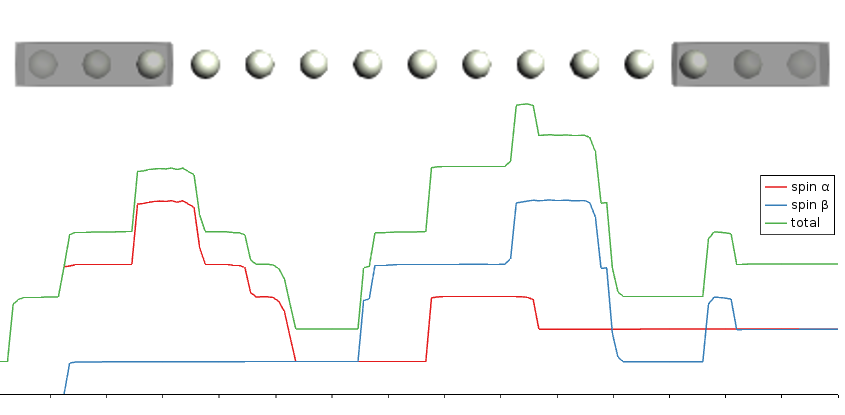
Spin transport in Chromium wire
Keywords: BAND, NEGF (Non-Equilibrium Green’s Function), metal wire, spin, transmission function, current
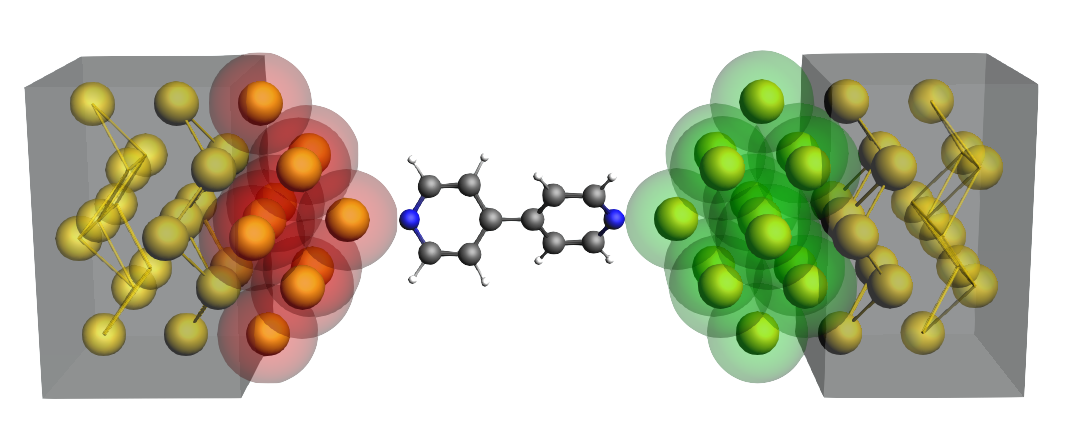
NEGF: Create a Molecular Junction
Keywords: DFTB, organic electronics, NEGF (Non-Equilibrium Green’s Function), metal wire, gate potential, tip, transmission function, current
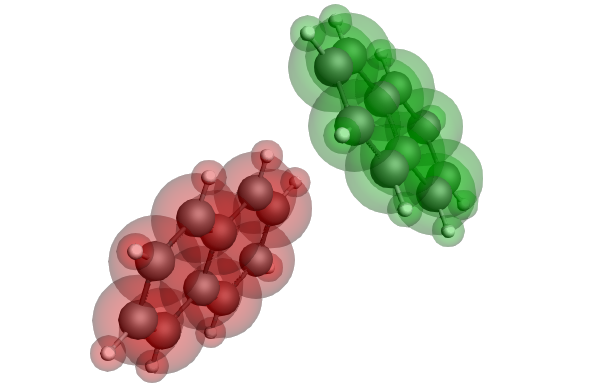
Electron and hole mobilities in organic electronics: charge transfer integrals
Keywords: ADF, charge transfer integrals, electronic coupling, Marcus theory, reorganization energies, hopping rates, field-effect transistors (OFETs), light-emitting diodes (OLEDs) and photovolatic cells (OPVs), effective mass tensor
Band Structure and Effective Mass Tensors of Phosphorene
Keywords: BAND, nanomaterials, electronic band structure, band gap, effective mass