DFT for Inorganic Chemistry
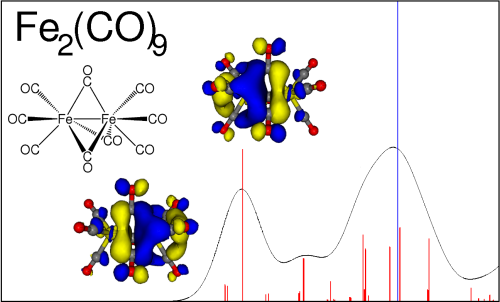
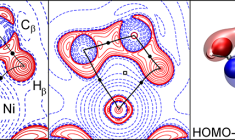
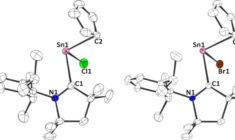
From its inception in the 1970s, ADF has been a powerful density functional theory code for studying inorganic compounds, such as transition metal and organometallic complexes. The relativistic effects which are at play in these molecules are accurately and efficiently treated with the ZORA Hamiltonian. ADF and the Amsterdam Modeling Suite are especially well-suited to understand chemical bonding interactions and spectroscopic properties of such compounds.