Recommendations¶
Model Hamiltonian¶
Relativistic model¶
By default we do not use relativistic effects. The best approximation is to use spin-orbit coupling, however that is computationally very expensive. The scalar relativistic option comes for free, and for light elements will give very similar results as non-relativistic theory, and for heavy ones better results w. r. t. experiment. We recommend to always use this (scalar ZORA). To go beyond to the spin-orbit level can be important when there are heavy elements with p valence electrons. Also the band gap appears quite sensitive for the spin-orbit effect.
XC functional¶
The default functional is the LDA, that gives quite good geometries but terrible bonding energies. GGA functionals are usually better at bonding energies, and among all possibilities the PBE is a common choice. Using a GGA is not a lot more expensive than using plain LDA. For the special problem of band gaps there are a number Model Hamiltonians available (eg. TB-mBJ and GLLC-SC). The Unrestricted option will be needed when the system is not closed shell. For systems interacting through dispersion interactions it is advised to use the Grimme corrections. Unfortunately there is no clear-cut answer to this problem, and one has to try in practice what works best.
Technical Precision¶
The easiest way to control the technical precision is via the NumericalQuality key. One can also independently tweak the precision of specific technical aspects, e.g.:
BeckeGrid
Quality Good ! tweak the grid
End
KSpace
Quality Good ! tweak the k-space grid
End
ZlmFit
Quality Normal ! tweak the density fit
End
SoftConfinement
Quality Basic ! tweak the radial confinement of basis functions
End
Here are per issue hints for when to go for a better quality (but it is by no means complete)
BeckeGrid: Increase quality if there are geometry convergence problems. Also negative frequencies can be caused by an inaccurate grid.
KSpace: Increase quality for metals
ZlmFit: Increase quality if the SCF does not converge.
SoftConfinement: Increase quality for weakly bonded systems, such as layered materials
Performance¶
The performance is influenced by the model Hamiltonian and basis set, discussed above. Here follow more technical tips.
Reduced precision¶
One of the simplest things to try is to run your job with NumericalQuality Basic. For many systems this will work well, and it can be used for instance to pre-optimize a geometry. However, it can also cause problems such as problematic SCF convergence, geometry optimization, or simply bad results. See above how to tweak more finely the Technical Precision.
Memory usage¶
Another issue that is the choice CPVector (say the vector length of you machine) and the number of k-points processed together during the calculation of the parameters. In the output you see the used value
=========================
= Numerical Integration =
=========================
TOTAL NR. OF POINTS 4738
BLOCK LENGTH 256
NR. OF BLOCKS 20
MAX. NR. OF SYMMETRY UNIQUE POINTS PER BLOCK 35
NR. OF K-POINTS PROCESSED TOGETHER IN BASPNT 5
NR. OF SYMMETRY OPERATORS (REAL SPACE) 48
SYMMETRY OPERATORS IN K-SPACE 48
If you want to change the default settings you can specify the CPVector and KGRPX keywords. The optimal combination depends on the calculation, on the machine. Example
CPVector 512
KGRPX 3
Note: bigger is not necessarily better.
Reduced basis set¶
When starting work on a large unit cell it is wise to start with a DZ basis. With such a basis, one can test for instance the quality of the k-space integration. However, for most properties, the DZ basis is probably not very accurate. You can next go for the DZP (if available) or TZP basis set, but that may be a bit of overkill.
Performance on machines with many cores¶
When running a not so big system (1000 basis functions) on a single machine with many cores you may observe a large discrepancy between the cpu and the elapsed time.
In the logfile you see for instance
cyc= 1 err=1.99E+00 meth=m nvec= 1 mix=0.0750 cpu= 3s ela= 27s fit=3.75E-02
indicating that the cpu time is 3 seconds, but the ela(psed) time was 27 seconds, much longer.
The (likely) reason is the use of shared arrays when calculating the matrix elements, which requires locking within a node.
A way to avoid this problem is to emulate as if you are using multiple nodes. Say you have a 128 core machine and add to your script
export SCM_SHAR_NCORES=8
$AMSBINB/ams ...
and tell ams that a node is made of 8 cores. When you run the job (on a single node 128 core machine) you should see in the logfile
AMS 2020.203 RunTime: Jan16-2021 18:05:27 Nodes: 16 Procs: 128
and now it is as if you are running on 16 nodes with 8 cores each. This requires more memory but this only becomes an issue with large system (10000 basis functions). In this example we need 16 times as much memory. You can use other values for the SCM_SHAR_NCORES variable, and it also works when using more than one (physical) node.
Since ams2021 a physical node may already be split automatically when ams recognizes that it uses multiple slots.
Is memory an issue for your calculation? The number of basis functions is printed in the output
*******************************
* S C F P R O C E D U R E *
*******************************
Nr. of basis functions 1424
Nr. of core functions 592
Nr. of fit functions 0
Nr. of symmetry unique K-points 1
Valence charge 640.00
You take this number squared and multiply this with 16 (complex number) and you have the size of a single matrix. Then you multiply with 10 or 30 to get an estimate of the memory needed (per “node”). You should compare is to the memory per core times the nr, of cores per node.If it does not fit then the performance drop will be even more dramatic, as the system needs to swap.
Systems with many basis functions are either systems with many atoms (1000) or systems with heavy elements and a small core (gold slab).
Band gap calculations¶
The simplest method is to compare the difference between the HOMO and the LUMO to the experimental band gap. It is quite well known that regular GGAs, such as the PBE functional, underestimate the band gap this way. However, there are some functionals designed to make the HOMO LUMO gap resemble the experimental gap. These are either MetaGGAs or model potentials (for which there is no energy expression). When using MetaGGAs it is recommended to use a small frozen core, as the core orbitals will be calculated at the LDA level. The KSpace%Quality should be set to Good. The TZP basis set gives already good gaps.
We have calculated with these settings for some functionals the band gap on the Crowley test set (leaving out transition metal oxides and 2D slabs). The spin orbit change to the band gap was calculated only at the PBE level and used for all other functionals.
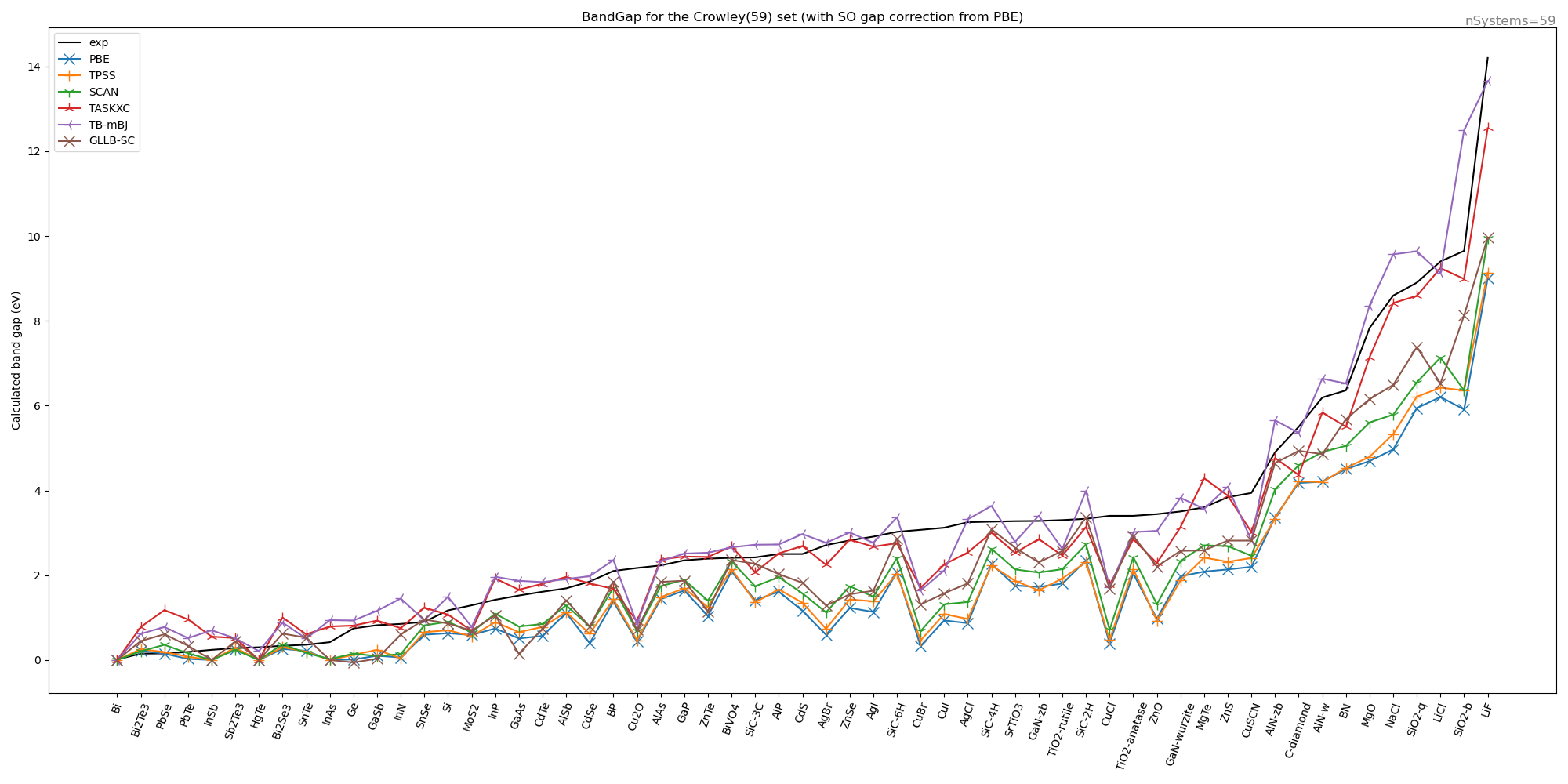
XC |
MAE |
MARE |
|---|---|---|
PBE |
1.374 |
0.520 |
TPSS |
1.288 |
0.489 |
SCAN |
1.042 |
0.425 |
TASKXC |
0.469 |
0.510 |
TB-mBJ |
0.462 |
0.414 |
GLLB-SC |
0.850 |
0.459 |
We can conclude that the TB-mBK functional appears to be best one, but the TASKXC is also doing quite well.
Here is the (Band engine) input used for the TASKXC functional
Basis Type=TZP Core=Small # for metaGGA a small core is recommended
KSpace Quality=Good
XC
metaGGA TASKXC
End
BandStructure Enabled=yes # this gives you also the gap estimated along the standard path through the BZ zone (in the text output)
The gap is either obtained from the kf file from the Variable BandStructure%BandGap, or from the text output.
in a plams script both can be obtained this way
try:
gap = job_result.readrkf("BandStructure","BandGap", "band")
gap=Units.convert(gap, 'hartree', 'eV')
except:
gap=0.0
try:
grep_string=job_result.grep_output('band gap from band-structure')
assert len(grep_string) == 1
words=grep_string[0].split(':')
gap_from_bs=float(words[-1].strip())
except:
gap_from_bs=0.0
Usually the difference is very small between the two methods.