Regression of NRTL parameters

In many cases, semi-empirical activity coefficient models, such as the NRTL (Non-random two-liquid) model, are more commonly available in engineering software, including process simulation tools. When experimental data is unavailable for a given binary mixture, it can be useful to derive NRTL parameters using activity coefficients from COSMO-RS/-SAC as reference data. This approach allows user to perform simulation by simply importing the fitted NRTL parameters.

The following script demonstrates how to generate a set of activity coefficients for a given mixture and utilize the optimization tools from the scipy library to obtain the optimal parameters for the NRTL model.

In this example, we use the following equation for a binary mixture, adopting the expressions for binary interaction parameters and the non-randomness factor as used in Aspen Plus. The equation can be easily adjusted if a different form is preferred.

\[\begin{split}\begin{aligned} &ln\gamma_1 = x_2^2 \left[ \tau_{21} \left( \frac{G_{21}}{x_1 + x_2 G_{21}} \right)^2 + \frac{\tau_{12} G_{12}}{(x_2 + x_1 G_{12})^2} \right]\\ &\ln\gamma_2 = x_1^2 \left[ \tau_{12} \left( \frac{G_{12}}{x_2 + x_1 G_{12}} \right)^2 + \frac{\tau_{21} G_{21}}{(x_1 + x_2 G_{21})^2} \right]\\ &Where: \\ &G_{ij} = exp(-\alpha_{ij} \tau_{ij})\\ &\tau_{ij} = a_{ij} + b_{ij} / T + e_{ij} ln(T) + f_{ij} T\\ &\alpha_{ij} = c_{ij} + d_{ij} (T-273.15)\\ \end{aligned}\end{split}\]

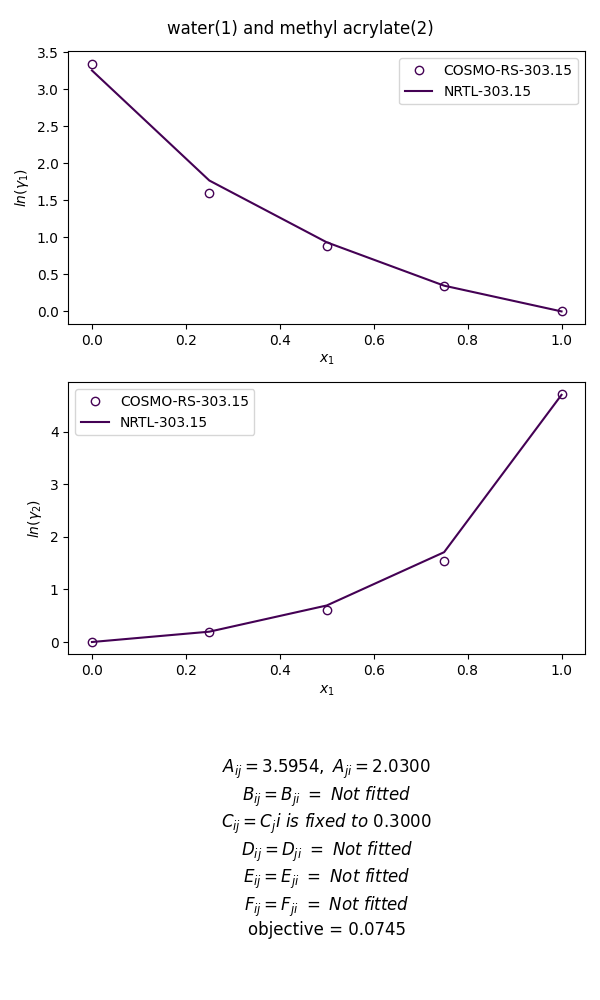
The figure below illustrate the regression for the mixture of water and methyl acrylate at 303K, using a fixed value of non-randomness factor at 0.3. The optimal interaction parameter obtained are 3.595 and 2.030, which are close to the value of 3.464 and 3.563 derived from experimental data regression reported in the literature [1].

/scm-uploads/doc/COSMO-RS/_images/fig_NRTL_differential_evolution.png

Python code

[show/hide code]
from pyCRS.CRSManager import CRSSystem
from pyCRS.Database import COSKFDatabase
from scm.plams import config, JobRunner
import numpy as np
import random
import sys
from scipy import optimize
import matplotlib.pyplot as plt
import matplotlib.cm as cm


def objective(params, ref_data, coef_fitted=None, coef_asymmetric=None, Cij=None, inf_weight=1.0):
    """
    Evalue the error between calculated and reference activity coefficients.
    Parameters :
        params (list of float) : Parameters used for model calculations.
        ref_data (dict) : Reference data containing reference activity coefficients.
        coef_fitted (dict, optional) : Flags indicating which coefficients to include in the fitting.
        coef_asymmetric (dict, optional) : Flags indicating asymmetric of a coefficient.
        Cij (float, optional): Fixed Cij paramter in model calculation.
        inf_weight (float, optional) : weighting apply to infinite dilute activity coefficient.

    Returns:
        float : The total weighted error between calculated and reference activity coefficients.

    """
    if coef_fitted is None:
        coef_fitted = {"A": True, "B": False, "C": True, "D": False, "E": False, "F": False}

    if coef_asymmetric is None:
        coef_asymmetric = {"A": True, "B": True, "C": False, "D": False, "E": True, "F": True}

    lng1_calc, lng2_calc = compute_gammas_binaries(params, ref_data, coef_fitted, coef_asymmetric, Cij)

    weight_lng1 = np.ones(len(ref_data["temperature"]))
    weight_lng2 = np.ones(len(ref_data["temperature"]))

    if inf_weight != 1.0:
        inf1_mask = ref_data["x1"] == 0.0
        weight_lng1[inf1_mask] = inf_weight

        inf2_mask = ref_data["x1"] == 1.0
        weight_lng2[inf2_mask] = inf_weight

    errors = np.sum(weight_lng1 * np.power(lng1_calc - ref_data["lngamma1"], 2.0) + weight_lng2 * np.power(lng2_calc - ref_data["lngamma2"], 2.0))

    return errors


def compute_gammas_binaries(params, ref_data, coef_fitted, coef_asymmetric, Cij=None):
    lng1_calc = np.zeros(len(ref_data["temperature"]))
    lng2_calc = np.zeros(len(ref_data["temperature"]))

    temperature_old = None
    for idx, (temperature, x1) in enumerate(zip(ref_data["temperature"], ref_data["x1"])):
        if temperature == temperature_old:
            pass
        else:
            tau_12, tau_21, alpha_12, alpha_21 = compute_interaction_parameters_binaries(params, coef_fitted, coef_asymmetric, Cij, temperature)
            temperature_old = temperature

        lng1_calc[idx], lng2_calc[idx] = NRTL_lngamma_binaries(x1, tau_12, tau_21, alpha_12, alpha_21)

    return lng1_calc, lng2_calc


def compute_interaction_parameters_binaries(params, coef_fitted, coef_asymmetric, Cij, temperature):
    idx = 0
    tau_12 = 0.0
    tau_21 = 0.0
    alpha_12 = 0.0
    alpha_21 = 0.0

    for key in coef_fitted.keys():
        if coef_fitted[key]:
            v1 = params[idx]
            if coef_asymmetric[key]:
                idx += 1
                v2 = params[idx]
            else:
                v2 = v1
            idx += 1

            if key == "A":
                tau_12 += v1
                tau_21 += v2
            elif key == "B":
                tau_12 += v1 / temperature
                tau_21 += v2 / temperature
            elif key == "E":
                tau_12 += v1 * np.log(temperature)
                tau_21 += v2 * np.log(temperature)
            elif key == "F":
                tau_12 += v1 * temperature
                tau_21 += v2 * temperature

            if key == "C":
                alpha_12 += v1
                alpha_21 += v2
            elif key == "D":
                alpha_12 += v1 * (temperature - 273.15)
                alpha_21 += v2 * (temperature - 273.15)

        if key == "C" and not coef_fitted["C"]:
            if Cij is not None:
                alpha_12 += Cij
                alpha_21 += Cij
            else:
                print(f"Regression stopped: Default Cij parameter is not provided.")
                sys.exit()

    return tau_12, tau_21, alpha_12, alpha_21


def NRTL_lngamma_binaries(x1, tau_12, tau_21, alpha_12, alpha_21):
    x2 = 1.0 - x1
    G_12 = np.exp(-alpha_12 * tau_12)
    G_21 = np.exp(-alpha_21 * tau_21)

    # Calculate activity coefficients
    lng1 = x2**2 * (tau_21 * (G_21 / (x1 + x2 * G_21)) ** 2 + tau_12 * G_12 / (x2 + x1 * G_12) ** 2)
    lng2 = x1**2 * (tau_12 * (G_12 / (x2 + x1 * G_12)) ** 2 + tau_21 * G_21 / (x1 + x2 * G_21) ** 2)

    return lng1, lng2


def summarize_coefficients(opt_res, coef_fitted, coef_asymmetric, Cij, display=False):
    params = opt_res.x
    errors = opt_res.fun

    idx = 0
    summary = []
    for key in coef_fitted.keys():
        if coef_fitted[key]:
            v1 = params[idx]
            idx += 1
            if coef_asymmetric[key]:
                v2 = params[idx]
                idx += 1
                summary.append(f"${key}_{{ij}} = {v1:.4f},\ {key}_{{ji}} = {v2:.4f}$")
            else:
                v2 = p1
                summary.append(f"${key}_{{ij}} = {key}_ji = {v1:.4f}$")

            if display:
                print(f"{key}ij = {v1:.4f}; {key}ji = {v2:.4f}")
        else:  # If the coefficient is not fitted
            if key == "C":
                summary.append(f"${key}_{{ij}} = {key}_ji\ is\ fixed\ to\ {Cij:.4f}$")
                if display:
                    print(f"{key}ij = {key}ji = {Cij:.4f}")
            else:
                summary.append(f"${key}_{{ij}} = {key}_{{ji}}\ =\ Not\ fitted$")

    summary.append(f"objective = {errors:.4f}")

    return "\n".join(summary)


def show_regression(opt_res, ref_data, coef_fitted, coef_asymmetric, Cij=None, figname="NRTL_regression.png", save=True):
    params = opt_res.x
    errors = opt_res.fun
    lng1_calc, lng2_calc = compute_gammas_binaries(params, ref_data, coef_fitted, coef_asymmetric, Cij)

    unique_temperature = np.unique(ref_data["temperature"])
    colormap = cm.get_cmap("viridis", len(unique_temperature))  # 'viridis' is just an example

    fig = plt.figure(figsize=(6, 10))
    ax1 = fig.add_subplot(311)
    ax2 = fig.add_subplot(312)
    ax3 = fig.add_subplot(313)

    for idx, temperature in enumerate(unique_temperature):
        used_mask = ref_data["temperature"] == temperature
        color = colormap(idx)

        ax1.plot(ref_data["x1"][used_mask], ref_data["lngamma1"][used_mask], "o", color=color, markerfacecolor="none", label=f"{ref_data['method']}-{str(temperature)}")
        ax1.plot(ref_data["x1"][used_mask], lng1_calc[used_mask], "-", color=color, label=f"NRTL-{str(temperature)}")

        ax2.plot(ref_data["x1"][used_mask], ref_data["lngamma2"][used_mask], "o", color=color, markerfacecolor="none", label=f"{ref_data['method']}-{str(temperature)}")
        ax2.plot(ref_data["x1"][used_mask], lng2_calc[used_mask], "-", color=color, label=f"NRTL-{str(temperature)}")

    ax1.set_xlabel(f"$x_{{1}}$")
    ax1.set_ylabel(f"$ln(\gamma_{{1}})$")
    ax1.legend()
    ax2.set_xlabel(f"$x_{{1}}$")
    ax2.set_ylabel(f"$ln(\gamma_{{2}})$")
    ax2.legend()

    summary = summarize_coefficients(opt_res, coef_fitted, coef_asymmetric, Cij)

    ax3.text(0.5, 0.5, summary, ha="center", va="center", fontsize=12)
    ax3.axis("off")

    plt.suptitle(f"{ref_data['compounds'][0]}(1) and {ref_data['compounds'][1]}(2)")
    plt.tight_layout()

    if save:
        if ".png" != figname[-4::]:
            figname = figname + ".png"
        plt.savefig(f"{figname}")
    plt.show()


def get_bounds(coef_fitted, coef_asymmetric, coef_bounds):
    bounds = []
    for key in coef_fitted.keys():
        if coef_fitted[key]:
            bounds.append(coef_bounds[key])
            if coef_asymmetric[key]:
                bounds.append(coef_bounds[key])

    return bounds


def get_initial_guess(bounds, seed=1):
    initial_guess = []

    np.random.seed(seed)

    for lower, upper in bounds:
        if lower is not None and upper is not None:
            random_number = random.uniform(lower, upper)
        else:
            random_number = random.random()

        initial_guess.append(random_number)

    return initial_guess


# create a COSKFDatabase
db = COSKFDatabase("my_db.db")
db.add_compound("Water.coskf")
db.add_compound("Methyl_acrylate.coskf")

# set up for parallel run
config.default_jobrunner = JobRunner(parallel=True, maxjobs=8)  # Set jobrunner to be parallel and specify the numbers of jobs run simutaneously (eg. multiprocessing.cpu_count())
config.default_jobmanager.settings.hashing = None  # Disable rerun prevention
config.job.runscript.nproc = 1  # Number of cores for each job
config.log.stdout = 1  # suppress plams output default=3

# create a CRSystem for generating reference activity coefficient data
cal = CRSSystem()

mixture = {}
c1 = "Water"
c2 = "Methyl acrylate"

mixture[c1] = 0.0
mixture[c2] = 1.0

temperature = 303.15
for x in np.linspace(0, 1, 5):
    mixture[c1] = x
    mixture[c2] = 1.0 - x
    cal.add_Mixture(mixture=mixture, temperature=temperature, database="my_db.db")

# execute calculation
cal.runCRSJob()

# retrive result and create the reference data
CRS_results = [out.get_results() for out in cal.outputs]

ref_data = {}
ref_data["compounds"] = np.array(CRS_results[0]["name"])
ref_data["temperature"] = np.array([res["temperature"] for res in CRS_results])
ref_data["x1"] = np.array([res["frac1"][0][0] for res in CRS_results])
ref_data["lngamma1"] = np.array([np.log(res["gamma"][0][0]) for res in CRS_results])
ref_data["lngamma2"] = np.array([np.log(res["gamma"][1][0]) for res in CRS_results])
ref_data["method"] = CRS_results[0]["method"]

# Specify the regression settings for the NRTL model
# Define whether to fit the coefficients in the equations for tau_ij and alpha_ij
# tau_ij = Aij + Bij / T + Eij * ln(T) + Fij * T
# alpha_ij = Cij + Dij * (T - 273.15)
coef_fitted = {"A": True, "B": False, "C": False, "D": False, "E": False, "F": False}
# Specify whether the coefficients are asymmetric (i.e., Aij ≠ Aji)
coef_asymmetric = {"A": True, "B": True, "C": False, "D": False, "E": True, "F": True}
# Set bounds for each coefficient during regression
coef_bounds = {"A": (-100, 100), "B": (-30000, 30000), "C": (0.0, 1.0), "D": (-0.02, 0.02), "E": (-10, 10), "F": (-10, 10)}

# Default value for Cij, if required
Cij = 0.3
# Cij = None

# Create bounds and inital guess for the parameters used in the regression
bounds = get_bounds(coef_fitted, coef_asymmetric, coef_bounds)
initial_guess = get_initial_guess(bounds, seed=1)

# regression using the method build-in scipy.optimize
opt_method = "L-BFGS-B"
opt_method = "differential_evolution"

if opt_method == "differential_evolution":
    opt_res = optimize.differential_evolution(objective, bounds=bounds, x0=initial_guess, args=(ref_data, coef_fitted, coef_asymmetric, Cij), maxiter=1000)
else:
    opt_res = optimize.minimize(objective, method=opt_method, bounds=bounds, x0=initial_guess, args=(ref_data, coef_fitted, coef_asymmetric, Cij), options={"maxiter": 100})

summarize_coefficients(opt_res, coef_fitted, coef_asymmetric, Cij, display=True)
figname = f"fig_NRTL_{opt_method}.png"
show_regression(opt_res, ref_data, coef_fitted, coef_asymmetric, Cij, figname)

References