Linear Transit, PES scan¶
The PES scan task in AMS allows users to scan the potential energy surface of a system along one or multiple degrees of freedom, while relaxing all other degrees of freedom. If only one coordinate is scanned, this kind of calculation is usually just called a linear transit. However, since AMS allows scanning of multiple coordinates, and linear transit is just a special case of such a calculation, the task is always called a PES scan in AMS.
A linear transit may be used for instance to sketch an approximate path over the transition states between reactants and products. From this a reasonable guess for the Transition State can be obtained which may serve as starting point for a true transition state search for instance.
The PES scan task is enabled by selecting it with the Task keyword:
Task PESScan
The PESScan block configures all details of the scan:
PESScan
CalcPropertiesAtPESPoints [True | False]
FillUnconvergedGaps [True | False]
ScanCoordinate
nPoints integer
Coordinate integer [x|y|z] (float){2}
Distance (integer){2} (float){2}
Angle (integer){3} (float){2}
Dihedral (integer){4} (float){2}
SumDist (integer){4} (float){2}
DifDist (integer){4} (float){2}
FromLattice
...
End
ToLattice
...
End
FromStrainVoigt (float){6}
ToStrainVoigt (float){6}
CellVolumeRange (float){2}
CellVolumeScalingRange (float){2}
LatticeARange (float){2}
LatticeBRange (float){2}
LatticeCRange (float){2}
End
End
The PESScan block needs to contain at least one ScanCoordinate block
specifying which coordinate to scan, and how many points (keyword nPoints)
to sample along this coordinate. By default, 10 points are sampled along each
scanned coordinate (including the start and end point of the scan).
Distance, angle, and dihedral angle coordinates¶
The coordinate descriptors are very similar to the constraint
descriptors in the Constraints block used by the geometry
optimization task, but are followed by two values delimiting the start and end
of the coordinates, instead of just a single value:
Coordinate atomIdx [x|y|z] startValue endValueMoves the atom with index
atomIdx(following the order in theSystemblock) along the a cartesian coordinate (x,yorz), starting atstartValueand ending atendValue(given in Angstrom).Distance atomIdx1 atomIdx2 startDist endDistScans the distance between the atoms with index
atomIdx1andatomIdx2, starting fromstartDistand ending atendDist, both given in Angstrom.Angle atomIdx1 atomIdx2 atomIdx3 startAngle endAngleScans the angle (1)–(2)–(3) between the atoms with indices
atomIdx1-3, as given by their order in theSystem%Atomsblock. The scanned angle starts atstartAngleand ends atendAngle, given in degrees.Dihedral atomIdx1 atomIdx2 atomIdx3 atomIdx4 startAngle endAngleScans the dihedral angle (1)–(2)–(3)–(4) between the atoms with indices
atomIdx1-4, as given by their order in theSystem%Atomsblock. The scanned dihedral starts atstartAngleand ends atendAngle, given in degrees.SumDist atomIdx1 atomIdx2 atomIdx3 atomIdx4 start endScans the sum of the distances R(1,2)+R(3,4) between the atoms with indices
atomIdx1-4, as given by their order in theSystem%Atomsblock. The values to be scanned start atstartand end atend, given in Angstrom.DifDist atomIdx1 atomIdx2 atomIdx3 atomIdx4 start endScans the difference between the distances R(1,2)-R(3,4) of the atoms with indices
atomIdx1-4, as given by their order in theSystem%Atomsblock. The values to be scanned start atstartand end atend, given in Angstrom.
Joint scan coordinates¶
Note that multiple of these coordinate descriptors can be combined within a
single ScanCoordinate block. This combines the individual coordinates into
one compound coordinate, i.e. all coordinates will transit together through
their respective ranges. In this way the symmetric stretch in water could be
scanned by specifying the following single ScanCoordinate block (assuming
that the oxygen atom is the first in the System%Atoms block):
ScanCoordinate
Distance 1 2 0.8 1.1
Distance 1 3 0.8 1.1
End
Multidimensional PES scan¶
A multidimensional PES scan can be performed by specifying multiple
ScanCoordinate blocks in the input. To scan the space spanned by the bending
and symmetric stretch modes in water, one would use the following scan
coordinates:
ScanCoordinate
Distance 1 2 0.8 1.1
Distance 1 3 0.8 1.1
End
ScanCoordinate
Angle 2 1 3 90 130
End
In principle an arbitrary number of ScanCoordinate blocks can be combined to
specify the scanned configuration space. However, the total number of sample
points is the product of the number of points along all coordinates, and hence
grows quickly with the number of dimensions. Furthermore, only 1D (linear
transit) and 2D PES scans can be visualized in the GUI. We therefore suggest
sticking with <=2 dimensional PES scans. (Note that it is possible to constrain
additional degrees of freedom through the Constraints block. This could be
used to sample a few points along a third dimension “manually”, while still being
able to see the surfaces in the GUI.)
Lattice scan coordinates for periodic systems¶
Several ways to scan lattice degrees of freedom were added to the AMS2022.1 release.
Note that for each unit cell, a geometry optimization is performed. To keep the fractional
coordinates fixed during the PES Scan, set GeometryOptimization%MaxIterations to 0.
There can be only one scan coordinate for lattice degrees of freedom in a single PES scan job. Also note that scan coordinates for lattice degrees of freedom may not contain other coordinate descriptors within the same scan coordinate. Is is for example not possible to have a joint scan coordinate for a concerted lattice and bond length stretch.
It is, however, perfectly fine to combine a lattice scan coordinate with another scan coordinate for a two-dimensional PES scan.
See also
Example input files for PES scan jobs with lattice degrees of freedom.
Important
If you use k-space sampling (e.g., with BAND or DFTB), then the k-space grid is determined for the input structure, which is not necessarily any of the sampled points.
Isotropic scaling of the unit cell volume or area¶
CellVolumeScalingRange startValue endValueIsotropic scaling of the unit cell. Example:
CellVolumeScalingRange 0.9 1.1will scale the volume between 90% and 110% of the original unit cell. For 2D-periodic crystals, the area will be scaled instead.CellVolumeRange startValue endValueIsotropic scaling of the unit cell. Example:
CellVolumeRange 300 500will scale the volume between 300 ų and 500 ų for a 3d-periodic system. For 2D-periodic systems, the area will be scaled between 300 Ų and 500 Ų.
Scaling of the lattice vector lengths¶
These options keep the angles between lattice vectors fixed.
LatticeARange startValue endValueScans the length of the first lattice vector. Can be combined with the LatticeBRange and LatticeCRange keywords, but no other coordinates within the same ScanCoordinate. Unit: angstrom.
LatticeBRange startValue endValueScans the length of the second lattice vector. Can be combined with the LatticeARange and LatticeCRange keywords, but no other coordinates within the same ScanCoordinate. Unit: angstrom.
LatticeCRange startValue endValueScans the length of the third lattice vector. Can be combined with the LatticeARange and LatticeBRange keywords, but no other coordinates within the same ScanCoordinate. Unit: angstrom.
Strain matrix in Voigt notation¶
- 3D crystal:
FromStrainVoigt xx yy zz yz xz xy,ToStrainVoigt xx yy zz yz xz xy The
FromStrainVoigtandToStrainVoigtkeywords need to be applied together. Example:FromStrainVoigt -0.1 -0.1 -0.1 -0.1 -0.1 -0.1,ToStrainVoigt 0.1 0.1 0.1 0.1 0.1 0.1- 2D crystal:
FromStrainVoigt xx yy xy,ToStrainVoigt xx yy xy The
FromStrainVoigtandToStrainVoigtkeywords need to be applied together. Example:FromStrainVoigt -0.1 -0.1 -0.1,ToStrainVoigt 0.1 0.1 0.1- 1D crystal:
FromStrainVoigt xx,ToStrainVoigt xx The
FromStrainVoigtandToStrainVoigtkeywords need to be applied together. Example:FromStrainVoigt -0.1,ToStrainVoigt 0.1
Scan arbitrary lattices¶
Scan arbitrary lattices specifying the initial and final lattice vectors, using the same format as in the System%Lattice block. The PES scan will then interpolate the lattice vectors linearly between these two values:
ScanCoordinate
FromLattice
! lattice vectors as in System%Lattice
End
ToLattice
! ...
End
End
Calculate properties for all PES points¶
By default the engine result files for the individual PES points are not saved
on disk, as this can easily lead to huge amounts of data to be stored. This
behavior can be changed with the PESScan%CalcPropertiesAtPESPoints keyword:
PESScanCalcPropertiesAtPESPoints- Type:
Bool
- Default value:
No
- Description:
Whether to perform an additional calculation with properties on all the sampled points of the PES. If this option is enabled AMS will produce a separate engine output file for every sampled PES point.
Note that this performs a full single point calculation on every sampled PES
point, including the calculation of any PES point
properties selected in Properties block.
Troubleshooting¶
Technically all PES scan calculations are conducted as a series of geometry optimizations with constraints for the scanned coordinates, where the value of the constraint varies slowly through the scanned range. In this way every sampled point on the potential energy surface corresponds to a particular set of constraints. As with any geometry optimization, it can happen that an optimization towards a particular point on the potential energy surface does not converge. This is the most common problem encountered during PES scan calculations.
Since PES scans are implemented as a series of geometry optimizations, they are
influenced by the settings used for the geometry optimizer, e.g. its convergence
thresholds and the maximum number of steps before an optimization is considered
to have failed. The optimizer is configured in the GeometryOptimization
block, see the page on geometry optimization in the
AMS manual.
While tweaking the geometry optimizer’s settings can sometimes help with convergence problems, these problems can also be easily caused by errors in the user input.
A very common problem is that the geometry in the input, i.e. the System
block, is incompatible with the starting values of the scanned coordinates. This
would for example be the case if one wants to scan a dihedral angle from 0 to 90
degrees, but the actual angle on the input geometry is close to 90 degrees. In
this case it would be better to flip the scanned range from 90 to 0 degrees, so
that the input geometry already close to the first sampled point on the PES.
Otherwise the optimization for the first point has to cross a very long distance
on the PES, making convergence much harder. AMS automatically detects this and
prints a warning. We generally advise preparing the input geometry for a PES
scan by first running a geometry optimization with constraints set to lower
bound of the scanned coordinate intervals.
For multidimensional PES scans the order in which the PES points are visited
depends on the order in which the scanned coordinates are specified, i.e. the
order of the ScanCoordinate blocks in the input. Generally, the order in
which the PES points are visited is such that the coordinate which was specified
in the first ScanCoordinate block varies slowest. This is illustrated in
the following figure:

Here the scan starts at point 1(1,1) at the bottom left corner of the PES
and first moves along the entire range of the 2nd scan coordinate, before taking
a step along the 1st coordinate to point 6(2,1). The same PES points could
be visited in a different order (and under different names) if the order of the
two ScanCoordinate blocks is reversed in the AMS input:
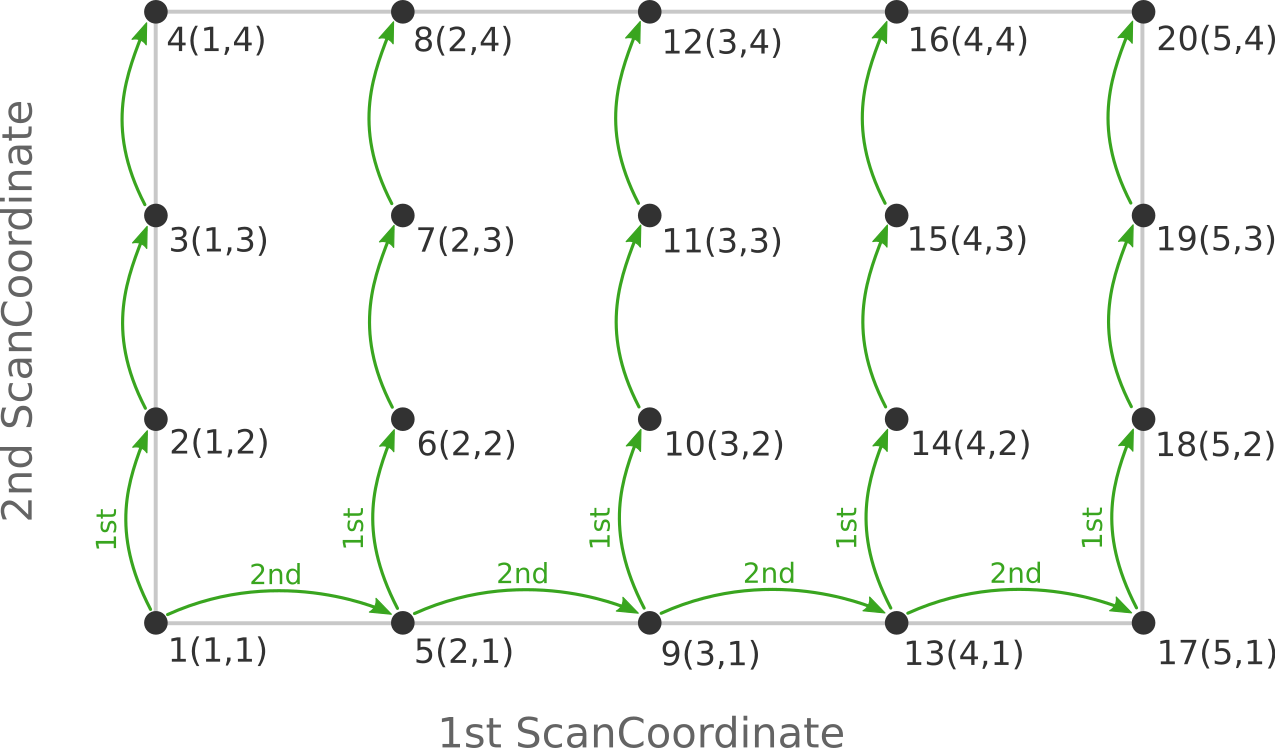
Depending on the shape of the scanned potential energy surface a particular order of visiting the PES points might be easier or harder for the optimizer, and convergence problems can sometimes be fixed by simply changing the order of the scanned coordinates. In the example above, it might be that scanning along the “vertical” direction is “harder” than scanning along the “horizontal” direction. In this case one should use the scan order from the first picture, which has only three “vertical” steps (whereas the other scan order has 15).
Note that AMS has a little safe-guard built in to help with PES scan convergence
issues: If the optimization towards a particular PES point did not succeed in
the initial attempt, AMS will later try again, but starting from a different
(converged) point close to unconverged one. This “PES gap filling” happens at
the very end of the calculation, after the initial scan has been completed. This
gap filling step is enabled by default, but can be controlled with the
PESScan%FillUnconvergedGaps keyword:
PESScanFillUnconvergedGaps- Type:
Bool
- Default value:
Yes
- Description:
After the initial pass over the PES, restart the unconverged points from converged neighboring points.
Output¶
Results are printed to the text output and stored in the binary result file ams.rkf.
Most information is found in the PESScan section, which references the corresponding geometries from the History section via the PESScan%HistoryIndices entry.
- PESScan
Section content: Data related to the Potential Energy Surface (PES) Scan procedure.
PESScan%GOConverged- Type:
bool_array
- Description:
Whether the (constrained) optimization at the various PES scan points converged.
- Shape:
[nPoints]
PESScan%HistoryIndices- Type:
int_array
- Description:
The indices of the frames in the History section corresponding to the PES point values.
- Shape:
[nPoints]
PESScan%HistoryPESPoints- Type:
int_array
- Description:
?
PESScan%nPoints- Type:
int
- Description:
The total number of scanned PES points. This is the product of all nPoints(#) values.
PESScan%nPoints(#)- Type:
int
- Description:
Number of points along the corresponding scan coordinate.
PESScan%nScanCoord- Type:
int
- Description:
Number of (independent) coordinates along which the PES scan is performed.
PESScan%PES- Type:
float_array
- Description:
The total energy at each particular PES point.
- Unit:
hartree
- Shape:
[nPoints]
PESScan%PESCoords- Type:
float_array
- Description:
The values of all coordinates for each particular PES point.
- Shape:
[:, nPoints]
PESScan%RangeEnd(#)- Type:
float_array
- Description:
The final value(s) for the corresponding scan coordinate.
PESScan%RangeStart(#)- Type:
float_array
- Description:
The starting value(s) for the corresponding scan coordinate.
PESScan%ScanCoord(#)- Type:
string_fixed_length
- Description:
A human readable description of the scan coordinate.