Transition state search and characterization of a Ziegler Natta Catalyst¶
Introduction¶
Ziegler-Natta catalyzed polymerization¶
In this tutorial, you will learn how to locate the transition state (TS) for the insertion step of ethylene polymerization catalyzed by a homogeneous Ziegler-Natta catalyst.

Discovered by Karl Ziegler and first applied to polymerization by Giulio Natta, this class of catalysts soon became an industry standard for the production of various polyolefins. Consequently, Ziegler’s and Natta’s work was awarded a Nobel Prize in 1963. Nowadays, the industrial Ziegler-Natta polymerization of polyolefins is among the most important industrial processes.
In the following tutorial, we use the AMS driver and DFTB to locate and characterize the transition state of a Ziegler-Natta reaction and use these results to calculate an approximate rate constant. You are also encouraged to learn how to reuse these results to expedite follow-up ADF calculations for more accurate results.
Strategy¶
Consider the following Ziegler-Natta reaction:

We will use a two-stage approach to locate the transition state of this reaction:
Find an initial guess of the TS by scanning the potential energy surface (PES scan) along the bonds newly formed during the reaction (we will use a composite coordinate scan).
Optimize and characterize the initial TS guess (transition state search).
Geometry Setup with AMSinput¶
This section shows how to construct the geometry of the ethene-metallocenium (Cp2Zr+CH3- C2H4) complex in AMSinput.
xyz file of the ethene-metallocenium complexSee also
If you are not yet familiar with the editing tools in AMSinput, take a look at our Introduction to Building Structures.
 → Metal complexes → Sandwiches → Ferrocene Sandwich
→ Metal complexes → Sandwiches → Ferrocene Sandwich ) and add a carbon atom
) and add a carbon atomChange the angle between the two benzene rings:

Finally we can add a ethene molecule:
 type ethene
type ethene
We now want to pre-optimize the structure we just built:
 →
→ 
Settings for the Engine¶
In the course of this tutorial, the DFTB engine with the GFN-1xTB model and implicit Toluene solvation is used. This particular setup provides a good compromise between computational speed and accuracy well suited for this tutorial. Other engines, such as our DFT code ADF, will yield more accurate results but will require longer computation time.
Here are possible engine settings for this tutorial
For a GFN1-xTB DFTB calculation with implicit Toluene solvation use the following settings:

For a DFT calculation with ADF, try the following settings.

The pre-optimized geometries provided throughout this tutorial are optimized with DFTB. Make sure to re-optimize them when you switch to ADF.
Tip
To just confirm a TS with ADF, do not run a full frequency calculation! Instead use the much faster PES point characterization available under Properties -> IR (Frequencies) -> Characterize PES point
For a semiempirical calculation with MOPAC, we suggest starting with following settings
Settings for the AMS Driver¶
First, take a look at the reactants and the product in the following figure to identify the two required scan coordinates:
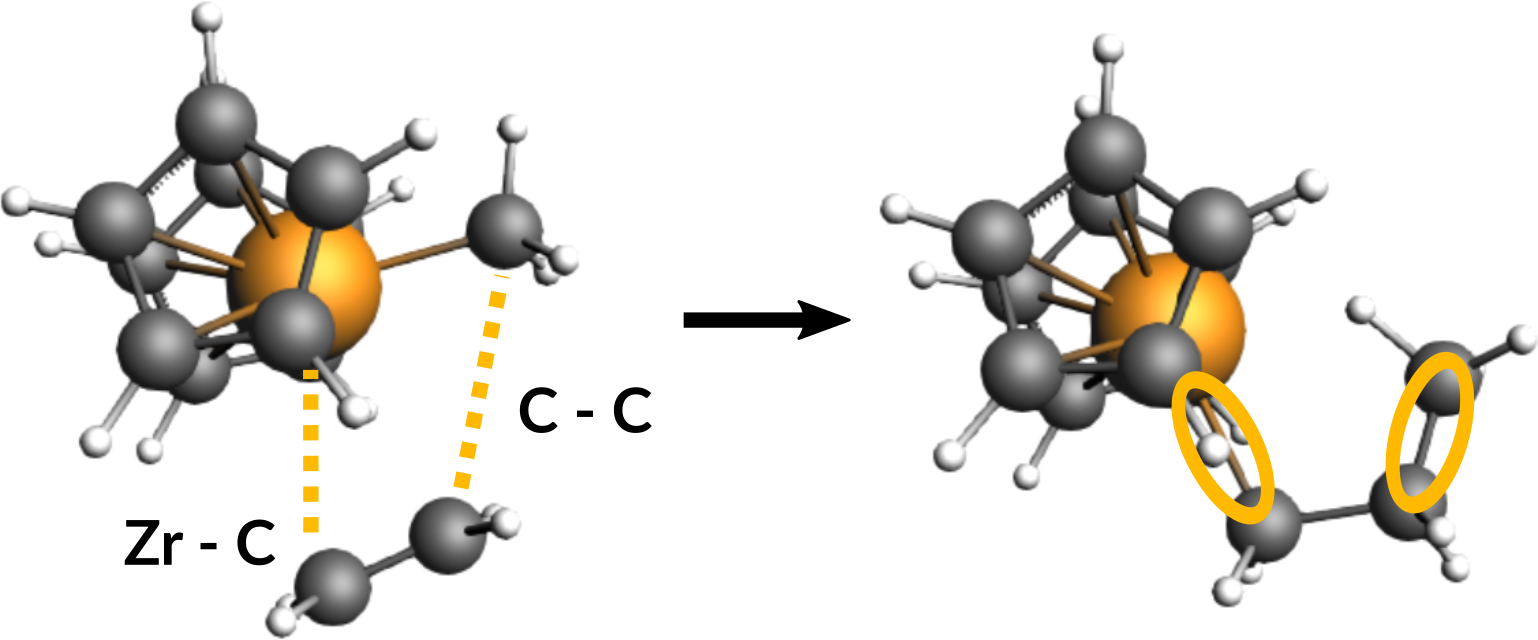
During the reaction, two bonds will be newly formed:
Zirconium-Carbon (between Zr-Ion and the ethene molecule)
Carbon-Carbon (between ethene molecule and methyl group)
These two distances will serve as scan coordinates and these will be scanned starting from their present values down to the distance of a typical Zr-C (measured from Zr-Methyl: ~2.3 Å) and Carbon-Carbon single bond (~1.5 Å).
Setup PES scan¶
To perform a PES scan, change the task in the main panel of the engine:
 next to the Task to specify the scan settings (or Model → Geometry Constraints and PES Scan)
next to the Task to specify the scan settings (or Model → Geometry Constraints and PES Scan)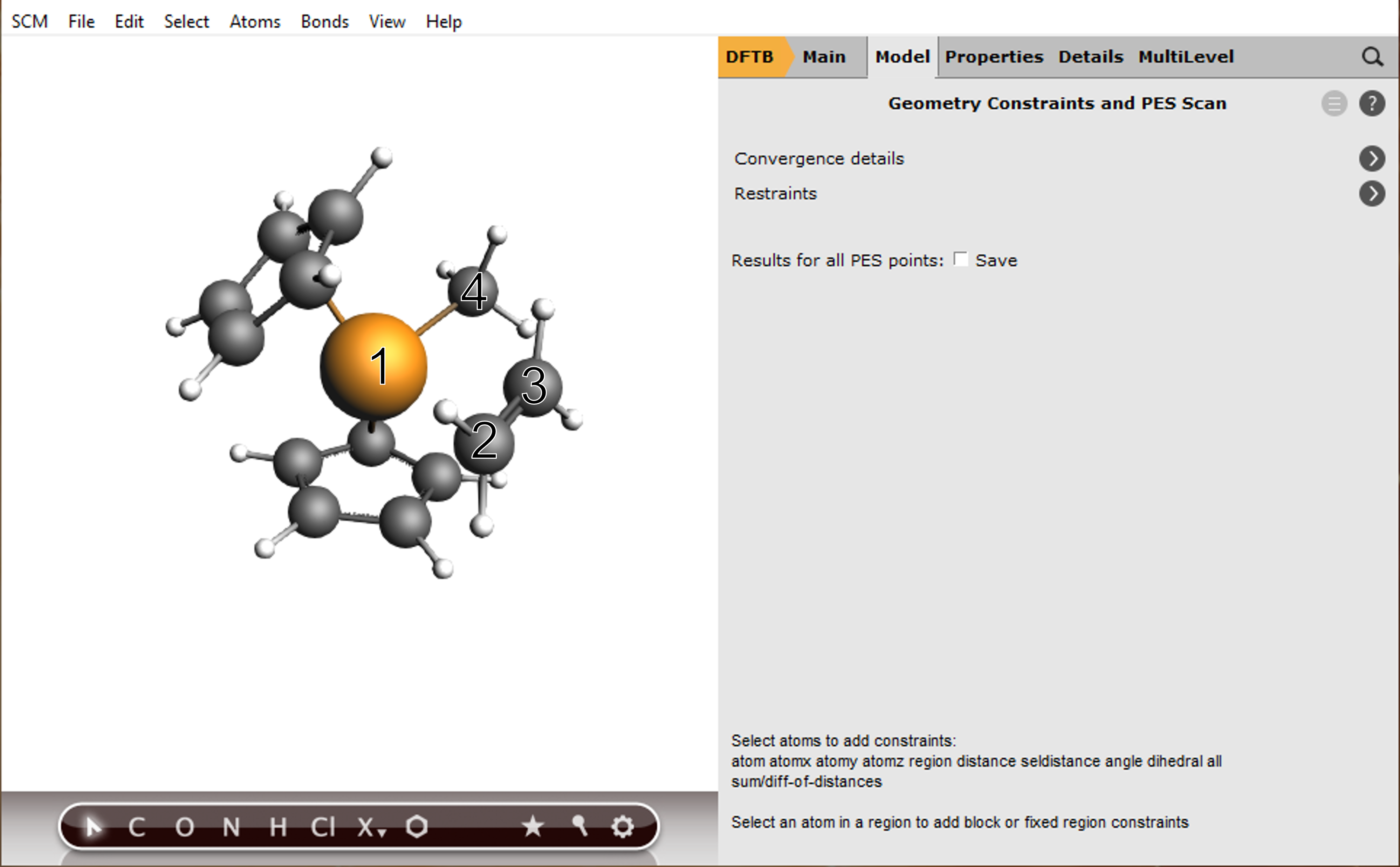
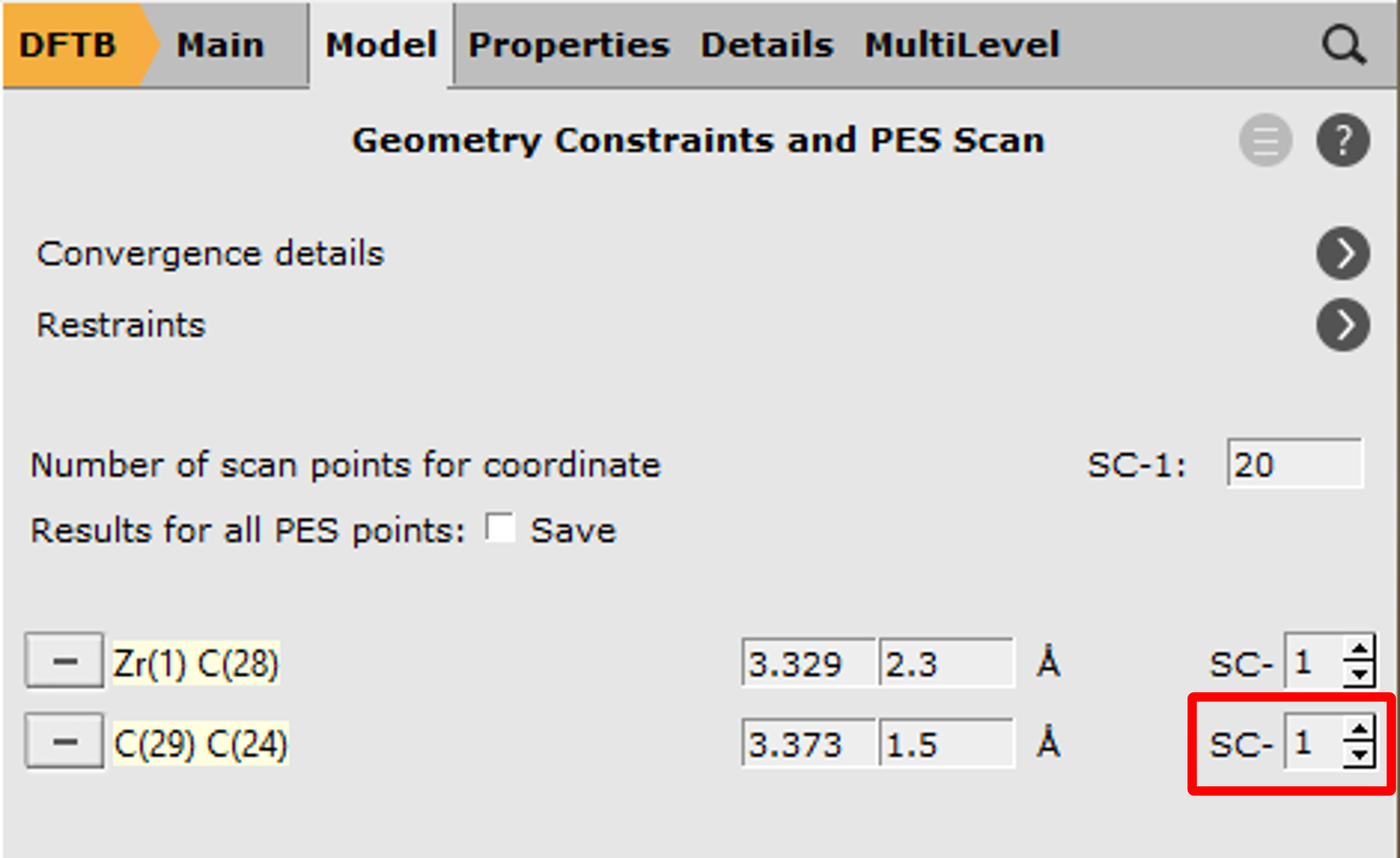
To add a scan coordinate, first select an atom pair
2.3 into the second field.1.5 into the second field for the Carbon atoms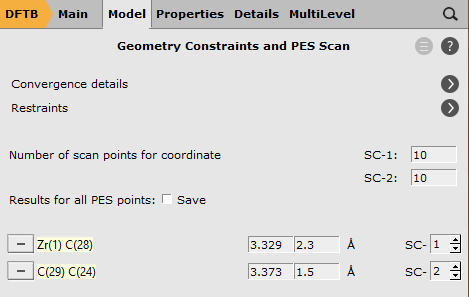
With these settings AMS will scan both coordinates independently, resulting in a 2D projection of the potential energy surface. However, with only one click you can combine the two distances into a single, composite coordinate:
20Note
This combination of coordinates implies a concerted formation of bonds. In a situation where this is not known beforehand an independent scan of the two coordinates might yield better results.
In the last step, loosen the convergence criteria of the geometry optimizer, since a fully converged path is not required at this point, but only a guess close to the transition state geometry.
 next to Convergence Details
next to Convergence Details0.0055.0e-55.0e-3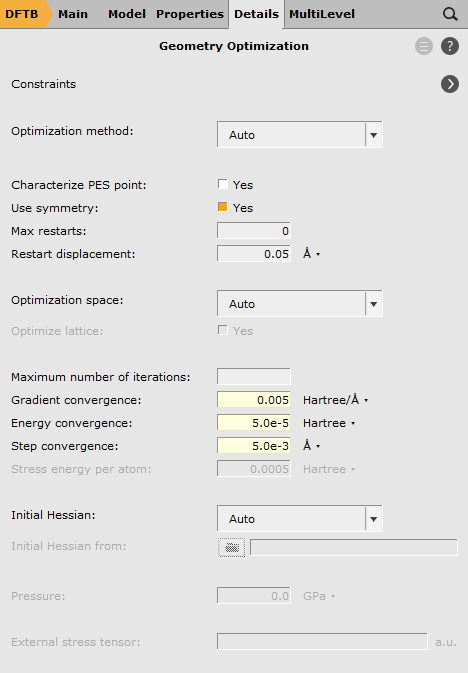
Now you only need to save and run the calculation. The progress can be monitored with AMSmovie.
At runtime, you will see all calculated geometries, including intermediates from the geometry optimizations. Once the PES scan is complete, these intermediates will be hidden. Depending on the AMS version you are using, you might need to close and reopen AMSmovie for this effect to take place. Your plots should roughly look as follows now
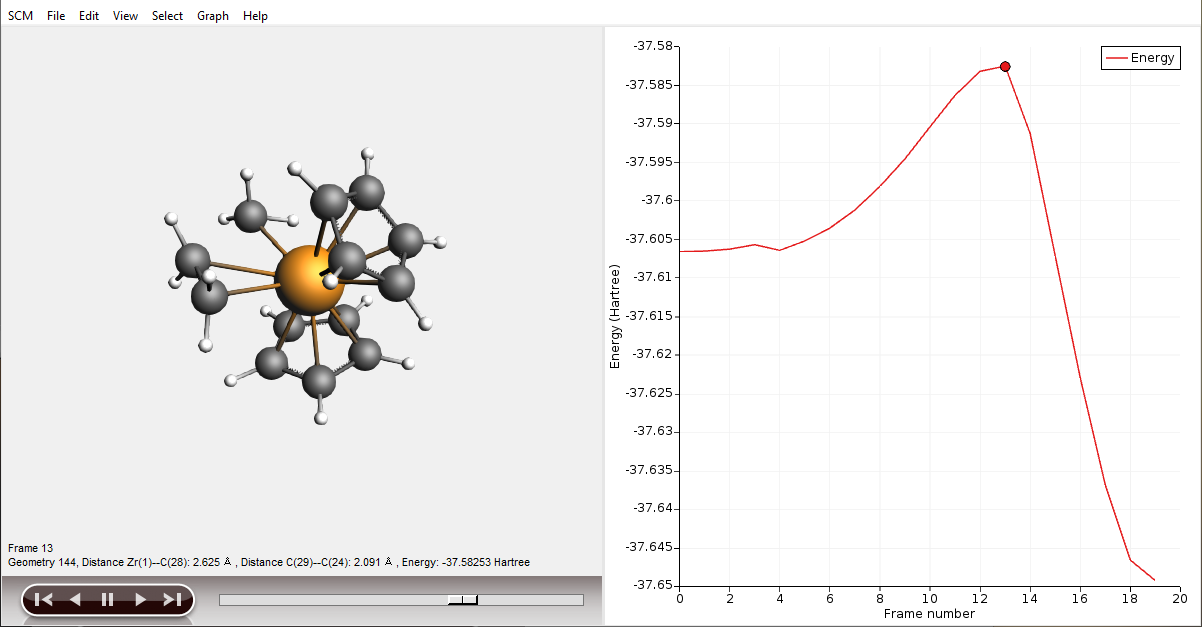
Use the scroll bar to navigate to the highest energy structure or click on the highest point in the energy curve. This geometry will serve as the initial guess for the transition state optimization!
From AMSmovie, save the structure with the highest energy
Transition State search¶
Tip
To ensure an efficient transition state search the starting geometry should be close to the expected TS. It furthermore helps to also have a good guess for the local curvature of the potential energy surface, e.g. from a frequency calculation. The Amsterdam Modeling Suite can provide such initial guesses and offers various methods for locating transition states.
A good overview of further strategies for more specific situations, tips & tricks is given in our slides Hands-On Transition State Search.
See also the AMS manual page on transition state search for more details.
We begin by importing the guess for the transition state saved from the PES scan explained in the previous section into AMSinput.

Tip
For DFT calculations on large systems, a much faster way of verifying that you found a transition state is the PES point characterization. This can be enabled in AMSinput in Properties → IR (Frequencies) → Characterize PES point.
The settings for the engine are the same as before: GFN-1xTB with a total charge of 1.0 and implicit Toluene solvation:
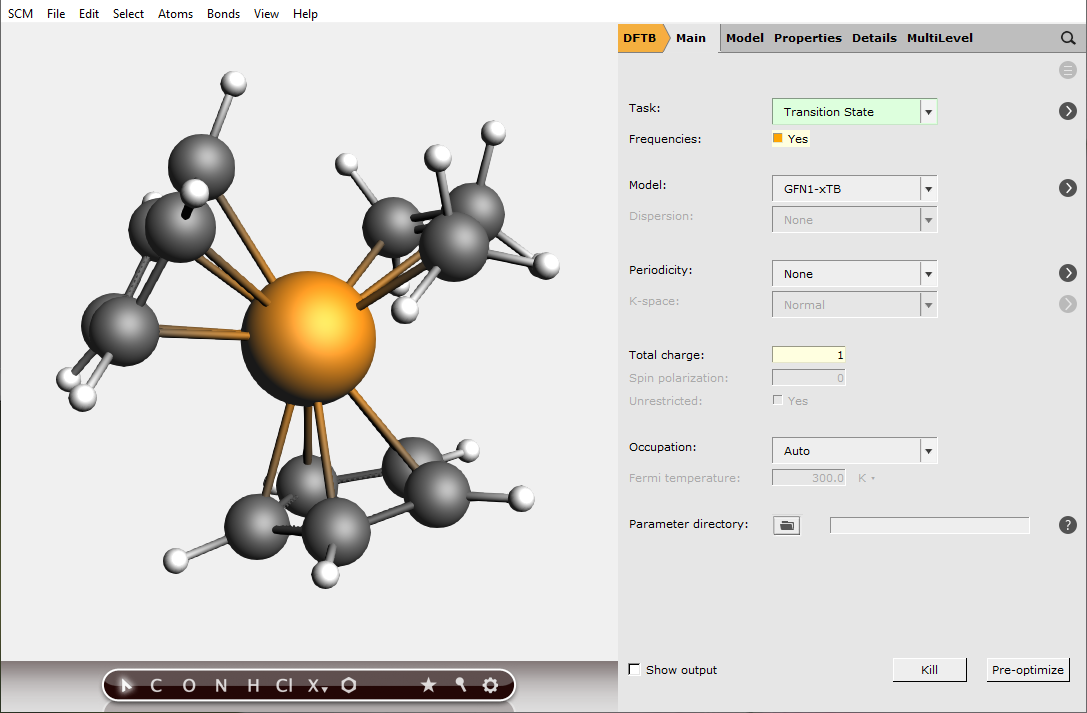
There exist several (approximate) options for the generation of an initial Hessian that is required for the transition state search. In this case, we shall start from the full Hessian evaluated at the initial guess for the transition state structure. This calculation can be requested with the option Calculate in the geometry optimization details panel:
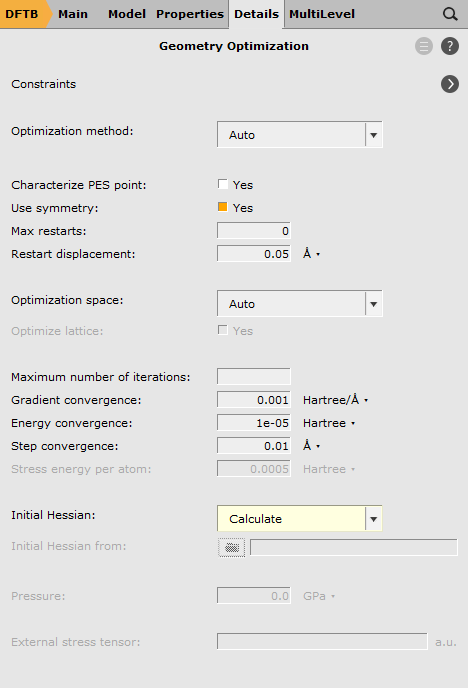
For a well-chosen starting structure, the transition state search should converge to the actual transition state geometry within a few iterations. Once the calculation is finished, open AMSspectra to inspect the calculated frequencies.
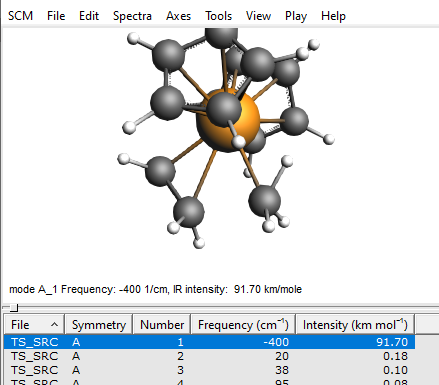
You should see only a single imaginary frequency indicated by a minus sign in the table of frequencies. If you do, then you have successfully optimized the transition state of this Ziegler-Natta reaction.
Tip
One might encounter additional imaginary modes due to either numerical artifacts or very shallow internal modes. In either case, the corresponding frequencies should be small (i.e. around -5 to -25 cm-1), in which case those modes can be ignored.
Results¶
Energies and barrier height¶
Once you have optimized a transition state, you can look at the energies to determine the reaction barrier height. You can find the Energy listed in the output file:
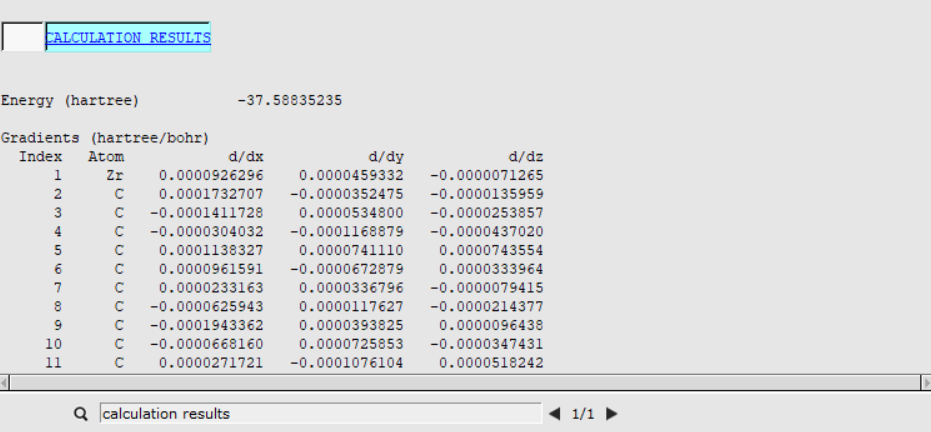
The Energy for the reactants was already calculated when you ran a geometry optimization of the ethene-metallocenium (Cp2Zr+CH3- C2H4) in the AMSinput Geometry Setup. In the corresponding output file it was found to be Ereactants= -37.6079 Hartree.
The barrier height for this reaction can now be calculated as the difference between these two energies \(E_\text{barrier}= E_\text{TS} - E_\text{reactants} = 0.01937 \text{[Hartree]} = 12.26 \text{[kcal/mol]}\)
Kinetics and Statistical Thermal Analysis¶
When asked to calculate frequencies, AMS will automatically calculate some useful thermodynamic properties such as entropy, internal energy, constant volume heat capacity, enthalpy, and Gibbs free energy from a statistical mechanics partition function. You can find more information on this in the corresponding section of the AMS manual . For now, we shall use these properties to calculate the rate constant.
Using Gibbs Free Energy of activation we can estimate the rate constant as described by the Eyring-Polanyi equation:
with the transmission coefficient \(\kappa\) assumed to be 1 (By setting \(\kappa = 1\), the resulting rate formula is commonly known as the Transition State Theory rate. This factor corrects for those reactive trajectories that recross the transition state and return without decomposing. It always reduces the reaction rate, so in general \(\kappa \le 1\)), the rate constant for this single step reaction can be calculated from the Gibbs Free Energy of activation ( \(\Delta G^{‡}\)).
To calculate \(\Delta G^{‡}\) we need to know the Gibbs Free Energy of both the transition state and the reactants.

The Free Energy of the transition state ( \(G_{\text{TS}}\) ) can be found in the thermodynamic properties section of the TS optimization output file:
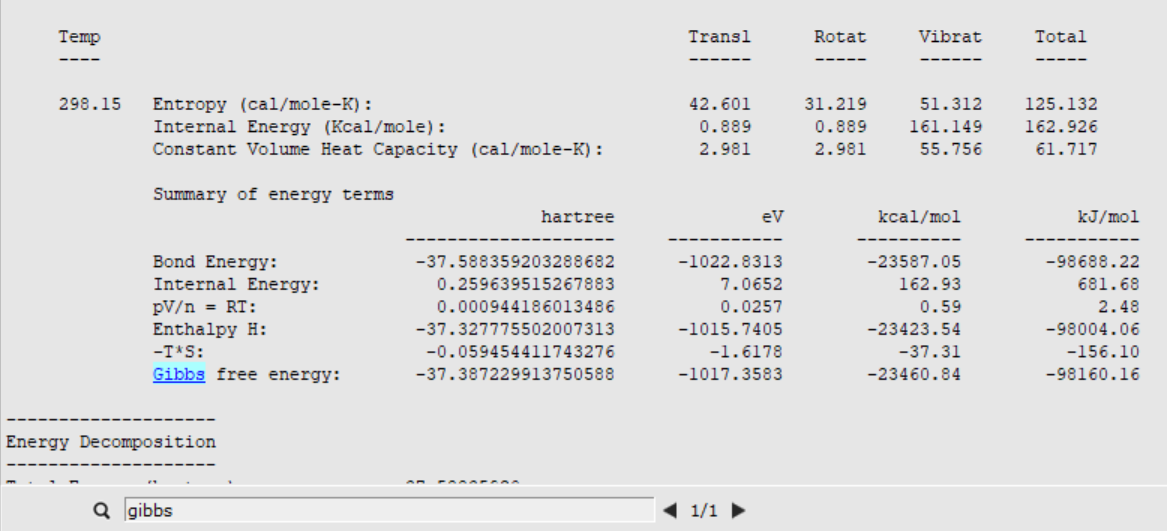
For the Gibbs Free Energy of the reactants a frequency calculation has to be carried out. Just download the optimized ethene-metallocenium structure and run a single point calculation to obtain the frequencies
With a resulting Gibbs Free Energy of
the Gibbs Free Energy of activation, \(\Delta G^{‡}\), becomes
and the Eyring-Polanyi rate constant at 295.15 K is calculated as
Workflows & Scripting¶
This optional section deals with the workflow automation of this tutorial. It assumes basic knowledge about the command line. If you have not used the command line with AMS before, take a look at our information on how to use the command line .
To execute the workflow:
ethene-metallocenium complex and place it into an empty directory.Ziegler_Natta.py and place into the same directory."$AMSBIN/plams" Ziegler_Natta.pySome results are printed to the command line. All results are found in the binary ams.rkf and dftb.rkf results files.
KF files can be opened and inspected with the GUI program KF Browser. They should only be viewed in Expert Mode:
The PLAMS scripts provided above demonstrate how to read results from these files. A short overview of relevant entries is provided in the tables below.
The PES scan calculation results can be obtained by using the AMSResults.get_pesscan_results() function. It provides gives a dictionary of the most common results from a PESScan. Alternatively, you can find in the KF file *.results/ams.rkf
Section |
Variable |
Meaning |
|---|---|---|
PESScan |
nScanCoord |
Number of independently scanned coordinates |
PESScan |
nPoints(1-nScanCoord) |
Number of points scanned for every scan coordinate |
PESScan |
RangeStart(1 until nScanCoord) |
Starting values for scan coordinate 1 (in Bohr) |
PESScan |
RangeEnd(1 until nScanCoord) |
End values for scan coordinate 1 (in Bohr) |
PESScan |
PESCoords |
Coordinates of the PES (in Bohr) |
PESScan |
PES |
Energies of the PES scan (in Hartree) |
PESScan |
History Indices |
Index of PES point geometries in section History |
The frequencies calculated after the transition state optimization are found in the engine specific results file. For DFTB this file is called *.results/dftb.rkf:
Section |
Variable |
Meaning |
|---|---|---|
AMS results |
Energy |
Final energy of the TS (in Hartree) |
Vibrations |
Frequencies |
Sorted list of final frequencies (in cm-1) |
You can also get the frequencies by using the AMSResults.get_frequencies() method.
The calculations can be run directly from a console input by executing the following run scripts:
ZN-PES-Scan.runfor the PES scanZN-TS-Opt.runfor the Transition State optimization
To run the scripts from the command line use the following commands
The results are then found in the corresponding output files ZN-PES-Scan.out and ZN-PES-TS-Opt.out
Note
If you running the scripts produces an error like /bin/sh^M: bad interpreter: No such file or directory, you need to convert the .run script from Windows to Unix line endings first. You can easily do that with dos2unix ZN-PES-Scan.run.