Oxidation of water on a Pt(111) surface¶
This tutorial will teach you how to
Optimize the lattice constants of a bulk material, cut a surface from it and optimize adsorbates
Do a thermochemical analysis for H2 and use these properties to estimate the potential for water oxidation over a Pt(111) surface
If at any point during the tutorial calculations fail, please consult the troubleshooting sections of either BAND or ADF.
Bulk Pt¶
We begin by setting up a geometry optimization job to build and optimize bulk Pt(111).
To create the Pt lattice structure
xyz file of bulk Pt →
→ 
See also
If you are not familiar with the editing tools in AMSinput, take a look at our introduction to Building Structures. Also refer to our introduction to Crystals and Surfaces for more information on how to build crystals and lattice structures.
 →
→ 
 button and select Cubic → fcc
button and select Cubic → fcc
Hint
Using the Periodic display  you can get a better view of the periodic system.
you can get a better view of the periodic system.
Now that the geometry is set up, we can run the optimization using the revPBE-D4(EEQ) XC-functional:
 button next to Task or in the panel bar open Details → Geometry Optimization
button next to Task or in the panel bar open Details → Geometry OptimizationThis will prompt you to save the job somewhere if you have not saved it already. The progress can be viewed in the log file viewer (SCM → Logfile) This calculation should take about 20 minutes on a modern laptop.
Once the calculation has finished, a pop-up will appear asking you to read in the new coordinates. Click Yes. Under Model → Lattice you can find the new lattice constant (2.79 Å). Remember, AMS defaults to the primitive cell. To convert to the conventional lattice constant, use the formula \(a_{\text{conventional}} = a_{\text{primitive}} \sqrt{2}\). This should give you approximately 3.95 Å, which closely matches the literature value of 3.92 Å. You can try to see for yourself that omission of relativistic effects will cause the lattice to expand quite significantly (4.16 Å). For more accurate relativistic effects, one could employ spin-orbit coupling effects as well, however these are more computationally demanding. You can visualize the band structure and density of states (DOS) by clicking on SCM → Band Structure and SCM → DOS respectively while in the output viewer.
OH and H2O on a Pt(111) surface¶
Next we cut a (111) surface from the optimized bulk structure.
xyz file of the Pt(111) surface button or choose in the menu bar, Edit → Crystal → Generate Slab
button or choose in the menu bar, Edit → Crystal → Generate Slab1 1 1 for the Miller indices field3 in the Number of layers field → Convert To Conventional Cell
→ Convert To Conventional CellSave this as a new file and run a single point calculation. Notice we are using the same settings as before.
Now we will put one monolayer (ML) of OH on the surface in the top position and set up the run.
To set up the geometry:
xyz file of the OH monolayer on a Pt(111) surface button
button0 0 2 ÅThe new structure should look something like this:

And to set up the calculation and run it:
 button next to Task or in the panel bar open Details → Geometry Optimization
button next to Task or in the panel bar open Details → Geometry Optimization
selected atoms (fixed position) button to freeze the atoms in placeIt will take a few cycles to finish. In the meantime we will prepare the optimization for a monolayer of water on Pt(111).
xyz file of the H2O monolayer on a Pt(111) surface280 pm (2.8 Å) by typing it in the white box at the bottom of the molecule drawing area, or use the scroll bar just below it.Remove bonds or press Delete. This would remove the selected Pt-O bond.0.0 0.0 3.8 and 0.0 1.0 2.5 Å.The new structure should look something like this:
Note that neither the 1 ML H2O nor the OH geometries are physically (chemically) meaningful. Water will typically adopt a hexagonal bilayer structure. Check out the references at the end of the tutorials for a starting point on more realistic geometries.
Save as a different file and run the job:
In the meantime, we will prepare calculations on free H2, H2O and OH, so that we can calculate their thermodynamic properties using ADF.
H2, H2O and OH molecules¶
We now continue with calculations on free H2, H2O and OH molecules. The general workflow is as follows:
 panel
panel button and click anywhere in the molecule drawing area to place a hydrogen atom
button and click anywhere in the molecule drawing area to place a hydrogen atom button at the bottom of the molecule drawing area. By right-clicking you may choose a different engine for preoptimization
button at the bottom of the molecule drawing area. By right-clicking you may choose a different engine for preoptimizationSelecting Frequencies will ensure that vibrational and thermodynamic properties of the systems are also calculated.

Run the job and repeat for H2O and OH by changing the structure of the molecule. For the OH calculation, please note that OH is a radical (doublet) species and you should ensure that you select the Unrestricted checkbox in the Main panel and enter 1 in the Spin polarization field.
Estimated water oxidation potential on Pt(111) surface from thermodynamical properties¶
We now have all the pieces available to estimate the minimum potential at which water can get oxidized over a Pt(111) surface:
where the starred species denote adsorbed molecules on the Pt(111) surface. Following Nørskov et al. (J. Phys. Chem. B, 108, 17886-17892 (2004)) we choose the standard hydrogen electrode as a reference potential, such that
is in equilibrium. We get the overall reaction
The free energy of the reaction is then:
The electrode potential \(U\) is incorporated as a linear energy shift \(qU = -U \text{eV}\) for every electron, giving
As a first approximation for the Gibbs free energies of OH* and H2O* we will just use the formation energies (from the atomic fragments). By far the largest contribution to the (difference in the) thermodynamic properties of the adsorbed species will be the zero-point energies (ZPEs), which can be crudely estimated from the gas phase frequency calculations for OH and H2O.
From the log file of the OH and H2O on Pt(111), write down the energy of formation near the end. (If necessary, look in the list of jobs in the AMSJobs window and click on the triangle in front of the job name so that all related files are listed. Double click on the .logfile files to open the appropriate logfile.)
from the H2 geometry optimization:
For the rotation and vibration contributions to \(\Delta G(\text{H}_2)\), we examine the more detailed output file (.out or Output from the SCM menu). The menu bars for the output viewer enable quick jumping through the calculation output. In this case we want the Gibbs free energy from Statistical Thermal Analysis which is located in the Other Properties menu.
and thus:
Consequently, the reaction over a Pt(111) layer will only take place when \(\Delta G < 0\). This is only true when we set the potential to at least \(U = 0.1494 \text{ V}\).
The calculated value is quite far from the experimental value of 0.8 V (Markovic and Ross, Surf. Sci. Rep. 45, 117 (2002)). Will including ZPE effects improve things? No: look in the output of the frequency calculations Other Properties → Zero-Point Energy:
so that the estimated \(\Delta\text{ZPE} = -0.3265 \text{ eV}\) for the gas phase species. Therefore, including \(\text{ZPE}\) would make it easier to oxidize water over Pt(111), reducing the oxidation potential. However, if you have some time left at the end of this tutorial, you can convince yourself that lower coverages will improve agreement with experiment:
Supercells for lower adsorbate coverage¶
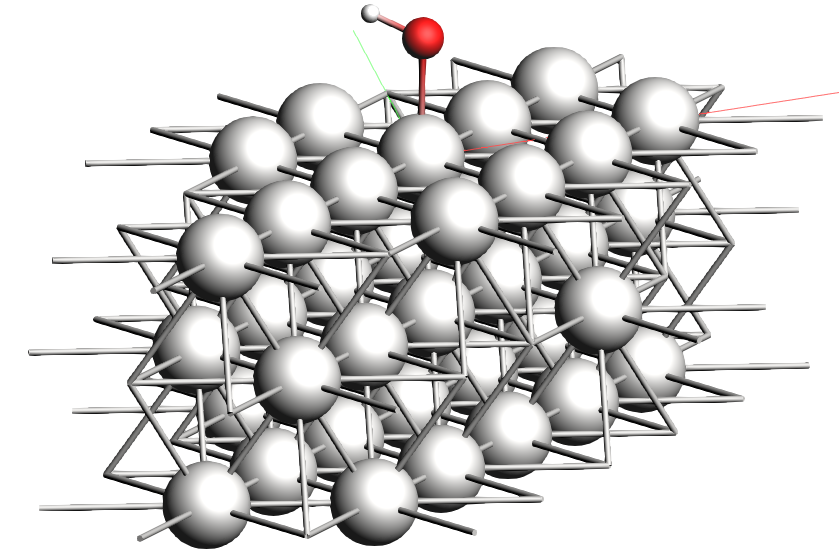
Alternatively, you could have started from the optimized OH* and H2O* 1 ML structures, making supercells from these and then removing two adsorbate molecules in the super cell. In this way we create a cell which has a third of the coverage of the 1ML layer.
These calculations should take about 2 and 6 hours to complete, so just run them overnight and read back the last formation energies from the logfile when you return tomorrow. These values (-77.9892 and -82.2107 eV for OH and H2O respectively) predict a much better water oxidation potential of about 0.8685 eV (with the same estimated gas phase \(\Delta \text{ZPE}\)).
Note¶
that this tutorial was just a short introduction to illustrate the calculation of thermodynamical properties of electrochemical half-reactions. In general for these kind of calculations you would want to converge carefully with respect to basis set, k-point sampling, and slab thickness. One should also carefully consider the adsorption geometry, e.g. water will want to form hexagon overlayers (necessitating √3 x √3 supercells).
All this goes too far to cover in a short tutorial session, but there are plenty of good literature examples where they have carefully considered these and more subtleties involved in these kind of calculations. Useful starting point are the papers by Nørskov and coworkers, for instance addressing oxygen reduction (2004) and water redox reactions on Pt(111) (2006).
BAND can also perform frequency calculations (more computationally demanding than ADF), so that ZPE effects can also be included for the adsorbed species rather than estimated from the gas phase. Finally, note that in BAND, uniquely, both solvation effects (COSMO) and homogeneous electric fields can be included properly (true 2D periodic systems). Both these effects will influence the adsorbate energies, and thereby the calculated oxidation potential.