Accurate XC functionals¶
This tutorial will show you how to use some of the accurate XC functionals in ADF that can be used for barrier heights, reaction energies, and non-covalent interactions: the fast r2SCAN-3c composite method, the accurate sigma-functional (σ-functional), a ‘general purpose’ double hybrid B2GPPLYP-D3BJ, and an opposite-spin-only double hybrid rev-DOD-PBEP86-D4, see also the section on XC functionals in the ADF manual. In this case for calculating a barrier height for a (water-catalyzed) proton-transfer reaction (one of the reactions in the WCPT18 [1] subset of the GMTKN55 database [2]).
The r2SCAN-3c composite method and the σ-functional were chosen because they have a parametrization specific for an STO basis set. B2GPPLYP-D3BJ and rev-DOD-PBEP86-D4 were chosen because of the well known precision one can get with double hybrids. The GMTKN55 database was mentioned to point out that one can find results for many different XC functionals in the literature that were validated against reference values that can be found in such databases. In literature one can also find recommendations for which XC functional to use in which situation. Note that in this tutorial only a few of the many XC functionals are highlighted that one can choose in ADF.
r2SCAN-3c¶
The r2SCAN-3c composite method [3] uses the \(r^2\) SCAN (r2SCAN) exchange-correlation functional, in combination with a tailor-made all electron polarized basis set (mTZ2P), the semiclassical London dispersion correction (D4), and a geometrical counterpoise (gCP) correction. NumericalQuality should be Good, and ZORA should be used. Note that internally LibXC will be used for the r2SCAN functional, and automatically the D4 and gCP corrections will be included. The STO-optimized r2SCAN-3c outperforms many conventional hybrid/QZ approaches in most common applications at a fraction of their cost. In ADF the r2SCAN-3c method can be used for, for example, geometry optimizations.
sigma-functional¶
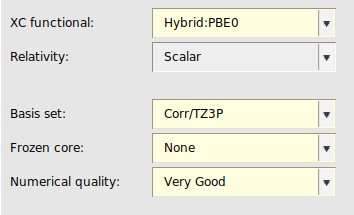
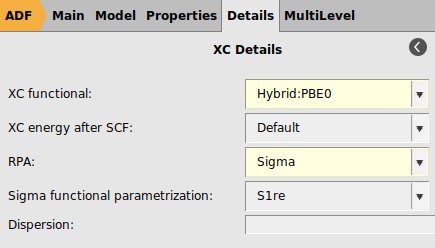
σ-Functionals belong to the class of Kohn–Sham (KS) correlation functionals based on the adiabatic-connection fluctuation–dissipation theorem and are technically closely related to the random phase approximation (RPA). ADF features a σ-functional implementation which is specifically parametrized for STO-type basis sets [4]. In particular, for the TZ3P basis one should use the S1re parametrization of the σ-functional. In Ref. [4] it was concluded that σ-functionals are highly promising alternatives to established density functionals, including double hybrid functionals. In ADF σ-functionals can only be used in single point calculations.
Remark, for QZ4P or QZ6P basis sets one should use the S1 parametrization of the σ-functional.
double Hybrids¶
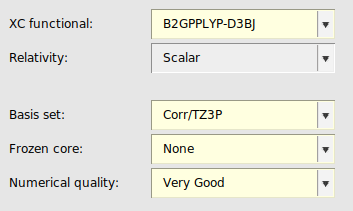
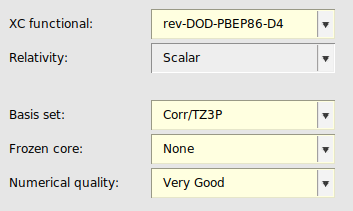
Double hybrids usually yield considerably better energies than (meta-)GGA and (meta-)hybrid functionals for (main group) thermochemistry and kinetics, transition metal chemistry and non-covalent interactions. B2GP-PLYP [5] is a ‘general purpose’ double hybrid. Rev-DOD-PBEP86-D4 [6] is an opposite-spin-only double hybrid. Opposite-spin only double hybrid functionals are recommended for large systems (50-100 atoms and larger) since they are computationally more efficient than the other double hybrid functionals which also include the same-spin contribution. For specific properties different double hybrids may be better, see literature. In ADF double hybrids can only be used in single point calculations.
Note that double hybrids converge much slower to the complete basis set limit than simpler DFT methods.
Calculation settings¶
AMSinput should then automatically set Basis set: mTZ2P, Frozen core: None, and Numerical quality: Good.

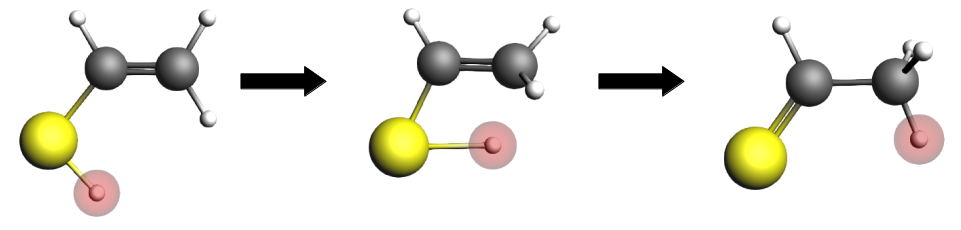
reac9 -> ts9 -> prod9¶

C 0.000000 0.759038 0.000000
H -0.781174 1.509717 0.000000
C 1.280382 1.112661 0.000000
H 2.084515 0.388850 0.000000
H 1.555670 2.157995 0.000000
H 0.468551 -1.541748 0.000000
S -0.688116 -0.859063 0.000000
Run the calculation:
Follow the same steps for “ts9”
C 0.468987 0.636874 0.053256
H 0.585413 1.716908 0.037321
C 1.515535 -0.285885 -0.030947
H 1.542575 -1.062299 0.729004
H 0.301002 -1.075601 -0.411970
H 2.498769 -0.002264 -0.395534
S -1.052181 -0.105168 -0.005792
And “prod9”
C 0.000000 0.617005 0.000000
H 0.517521 1.577301 0.000000
C -1.485898 0.714108 0.000000
H -1.957093 -0.265537 0.000000
H -1.819218 1.282178 0.874496
H -1.819218 1.282178 -0.874496
S 0.874587 -0.741425 0.000000
Note that the results for a specific XC functional for 1 example are not an indication of the precision of such XC functional in general.
barrier height |
reaction energy |
|
|---|---|---|
Ref [1] |
58.80 |
-2.44 |
r2-SCAN-3c |
54.1 |
-3.7 |
σ-functional (S1re) |
57.3 |
-2.2 |
B2GPPLYP-D3BJ |
59.0 |
-2.1 |
rev-DOD-PBEP86-D4 |
59.8 |
-1.9 |
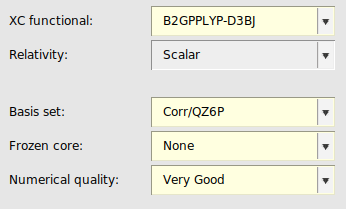
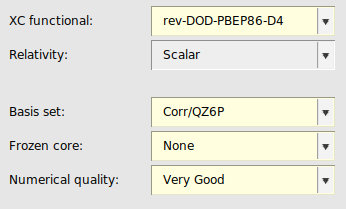
QZ6P basis set¶
Since double hybrids converge much slower to the complete basis set limit than simpler DFT methods, we include here also settings for the QZ6P basis set. Using r2SCAN-3c with a QZ6P basis set should not be done, since this composite method is defined only for a mTZ2P basis set. In case of the σ-functional with a QZ6P basis sets one should use the S1 parametrization, since the S1re parametrization of the σ-functional is only valid for TZ3P basis sets.
Remark, using a QZ6P basis set for the σ-functional or a double-hybrid is considered an expert option for reasons of numerical stability, see also the recommendations for MBPT calculations in the ADF manual.



Note that the results for a specific XC functional for 1 example are not an indication of the precision of such XC functional in general. Note also that the basis set effect for 1 example is not an indication of the basis set effect in general.
barrier height |
reaction energy |
|
|---|---|---|
Ref [1] |
58.80 |
-2.44 |
σ-functional (S1) |
59.5 |
-1.3 |
B2GPPLYP-D3BJ |
58.7 |
-2.5 |
rev-DOD-PBEP86-D4 |
59.6 |
-2.3 |