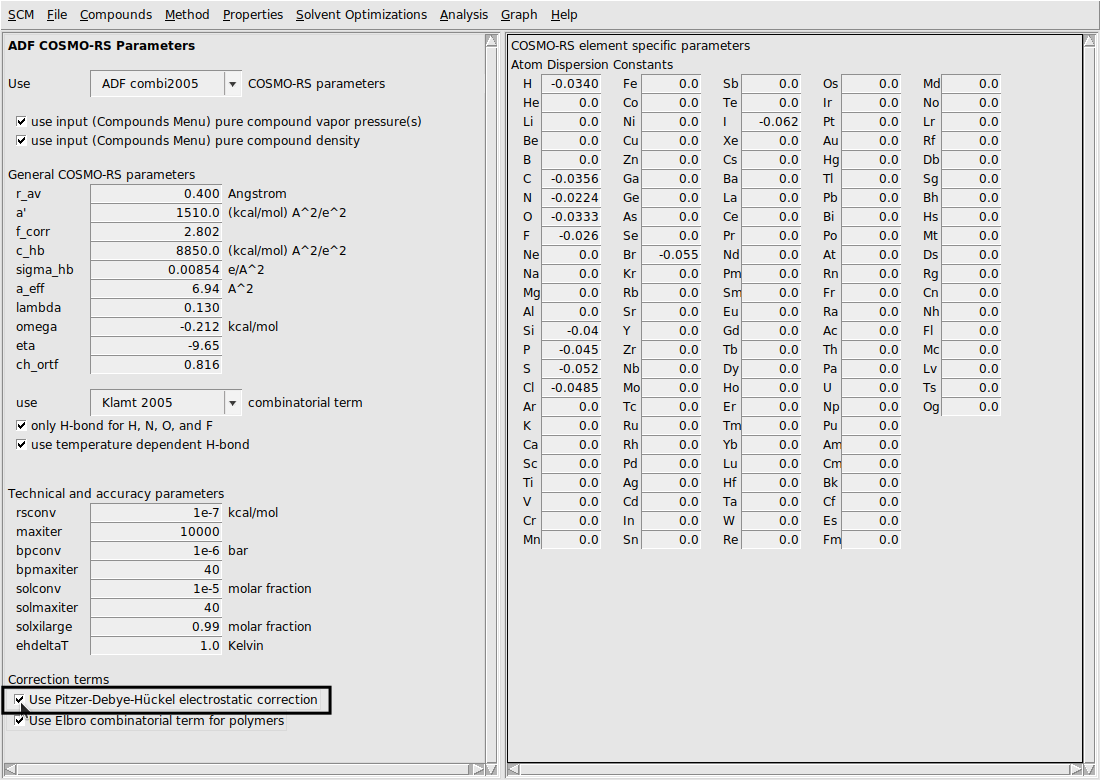
Pitzer-Debye-Hückel electrostatic correction

Systems with charged species often exhibit non-ideal behavior – even at low concentrations of ionic components. For this reason, it is often beneficial to include long range electrostatic corrections in the calculation of the activity coefficient. Several models for long range electrostatic energy exist, but one of the most successful and generalizable approaches is the Pitzer-Debye-Hückel (PDH) model 1.

This tutorial sets up a calculation for NaCl in water and compares (molality-based) mean ionic activity coefficients calculated by COSMO-RS to experiment. This tutorial will also perform the same calculation while not considering explicit water solvation (done with the multispecies tools of the ions and additionally while not using the PDH correction.

Turning the PDH correction on/off

By default the PDH correction is not used. It can be turned on (or back off) in the Parameters window. If the PDH correction is turned on, it will only have an effect if there are charged species detected in the system. The following steps more exactly describe how to adjust this parameter.

Method → Parameters
In the section Correction terms, (un)tick Use Pitzer-Debye-Hückel electrostatic correction
../_images/basic_input.png

Example: NaCl in Water

In this example, we will calculate mean ionic activity coefficients for a very common system: NaCl in water. Though it is possible to calculate the properties of this system with respect to NaCl as a single compound, it is more convenient for calculating mean ionic activity coefficients if we consider Na+ and Cl- as separate compounds. We will perform the calculations using the following 3 approaches:

  • Using only the bare (unhydrated) ions and no PDH correction

  • Using explicitly hydrated ions and no PDH correction

  • Using explicitly hydrated ions and the PDH correction

The user is invited to try to generate the structures necessary for this tutorial, but it is recommended to download the .coskf files in the link above. Using these .coskf files is more convenient and ensures consistency with the tutorial.

Calculating (molality-based) mean ionic activity coefficients

As ionic activity coefficients are more commonly reported as mean ionic activity coefficients, we’ll demonstrate how to perform the conversion here. Given a dissociation

\[A \rightarrow v^+ A^+ + v^- A^-\]

where \(v^+\) and \(v^-\) indicate the stoichiometric coefficients of the dissociation, the formula for mean ionic activity coefficients is the following:

\[\gamma^±_{A} = ( \gamma_{A^+}^{v^+} \gamma_{A^-}^{v^-} )^{\frac{1}{v^+ + v^-}}\]

In the case of NaCl, this is simply

\[\gamma^±_{NaCl} = \sqrt{ \gamma_{Na+} \gamma_{Cl-} }\]

For electrolytes, the reference state is often taken to be at infinite dilution in the solvent. Of course, in the limit of infinite dilution, the chemical potential goes to \(-\infty\), but we can use the chemical potential calculated with COSMO-RS (the so-called Ben-Naim chemical potential) as it contains no concentration term. We can then calculate the activity coefficients of each species as follows:

\[\gamma_i = \exp{ (\frac{\mu_i - \mu_i^*}{RT}) }\]

where \(\mu_i\) is the chemical potential of an ion calculated by COSMO-RS and \(\mu_i^*\) is the chemical potential of that ion at infinite dilution. Finally, to compare to experimental data, we’ll have to change to a molality scale for activity. That is done as follows:

\[\gamma_i^{(m)} = \frac{ \gamma_i^{(x)}}{1+(\nu^+ + \nu^-) 0.001 M_s m_i }\]

where \(\gamma_i^{(m)}\) is the molality-based (mean ionic) activity coefficient and \(\gamma_i^{(x)}\) is the mole fraction based activity coefficient. \((\nu^+ + \nu^-)\) is the count of the number of ions the salt dissociates into (2 for NaCl), \(M_s\) is the molar mass of the solvent (in g/mol), and \(m_i\) is the molality of the salt (in mol/kg):

\[m_i = \frac{x_i}{0.001 M_s(1-(\nu^+ + \nu^-)x_i)}\]

where \(x_i\) is the mole fraction of an ion.

(1) Using unhydrated ions without the PDH correction

We’ll first consider the simple case of dissociated Na+ and Cl- ions in water. To set up this experiment, first generate COSMO Result Files for Na+, Cl-, and Water (or simply use the water .coskf file in the database). Then setup a s1-s2 composition line calculation with the following:

Method → Parameters
In the section Correction terms, untick Use Pitzer-Debye-Hückel electrostatic correction
Properties → Solvents s1-s2 composition line
Choose 3 components
Enter the .coskf file for Na+ in the first box and set (s1,s2) to (0.1,0.0)
Enter the .coskf file for Cl- in the second box and set (s1,s2) to (0.1,0.0)
Enter the .coskf file for Water in the third box and set (s1,s2) to (0.8,1.0)
Change n to 10
Hit Run
Graph → Y axes → pure compound ln(activity coefficients)

This should result in the following

../_images/bare_ions_run.png

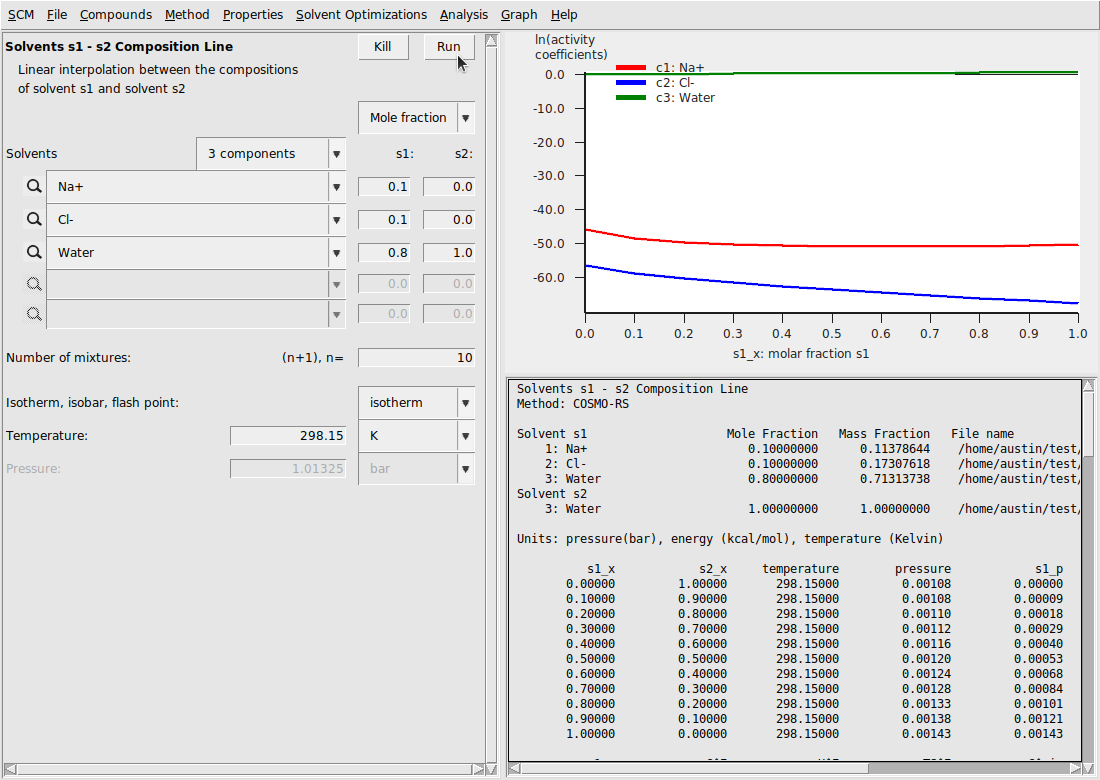
Template calculations for NaCl

In the output, navigate to Pure compound ln(activity coefficients)
Copy this section to a spreadsheet software for more convenient calculations

For the point \(s1\_x=0.0\) , we have \(\ln(\gamma)\) values for Na+ and Cl- at infinite dilution (these are -45.86 and -56.34, respectively). Next, we subtract these infinite dilution values from all the other \(\ln(\gamma)\) values to convert the standard state to infinite dilution of the ions. In steps, this is:

Subtract the value -45.86 from all subsequent \(\ln(\gamma)\) values for Na+
Subtract the value -56.34 from all subsequent \(\ln(\gamma)\) values for Cl-

We refer to the values after the subtraction as \(\ln(\gamma^*)\) values. Using these values, we can calculate the molarity mean ionic activity coefficient as follows:

\[\gamma^±_{NaCl} = \sqrt{ \exp(\ln(\gamma_{Na+}^*)) \exp(\ln( \gamma_{Cl-}^*)) }\]

Finally, this can be converted to molality based units with the following conversion:

\[\begin{split}\gamma^{±,(m)}_{NaCl} & = \frac{ \gamma^±_{NaCl} }{{1+(\nu^+ + \nu^-) 0.001 M_s m_i }} \\ & = \frac{ \gamma^±_{NaCl} }{{1+2*0.001 M_s * \frac{x_{Na+}}{(1-2*x_{Na+})*0.001 M_s} }} \\ & = \gamma^±_{NaCl} * (1-2 x_{Na+})\end{split}\]

Example calculations for the first few points

For the first point at finite dilution (\(s1\_x=0.1\), s1 has 0.1 molar fraction Na+, \(x_{Na+} = 0.1*s1\_x = 0.01\)), we use the \(\ln(\gamma)\) values for Na+ and Cl- (-48.36 and -58.66), the \(\ln(\gamma)^\infty\) values (-45.86 and -56.34), and the mole fraction of Na+ (0.01). These numbers can be used to calculate the molality based mean ionic activity coefficient as follows:

\[\begin{split}\gamma^{±,(m)}_{NaCl} & = \gamma^±_{NaCl} * (1-2 x_{Na+}) \\ & = \sqrt{ \exp\left(\ln(\gamma_{Na+})-\ln(\gamma_{Na+}^\infty)\right) \exp\left(\ln( \gamma_{Cl-}) - \ln(\gamma_{Cl-}^\infty)\right) } * (1-2 x_{Na+}) \\\end{split}\]

For \(s1\_x=0.1\), we have

\[\begin{split}\gamma^{±,(m)}_{NaCl}& = \sqrt{ \exp\left(-48.36--45.86\right) \exp\left(-58.66 - -56.34\right) } * (1-2 *0.01) \\ & = 0.089 \\ ln(\gamma^{±,(m)}_{NaCl})&=ln(0.089)= -2.42 \\ m_i & = \frac{0.01}{0.001 * 18.015 * (1-2*0.01)} = 0.57\end{split}\]

For \(s1\_x=0.2\), we have

\[\begin{split}\gamma^{±,(m)}_{NaCl}& = \sqrt{ \exp\left(-49.51--45.86\right) \exp\left(-60.23 - -56.34\right) } * (1-2 *0.02) \\ & = 0.022 \\ ln(\gamma^{±,(m)}_{NaCl})&=ln(0.022)= -3.82 \\ m_i & = \frac{0.02}{0.001 * 18.015 * (1-2*0.02)} = 1.16\end{split}\]

Repeating this procedure for the remainder of the points results in the following poor correspondence to experiment 2:

../_images/bare_ions_no_pdh.png

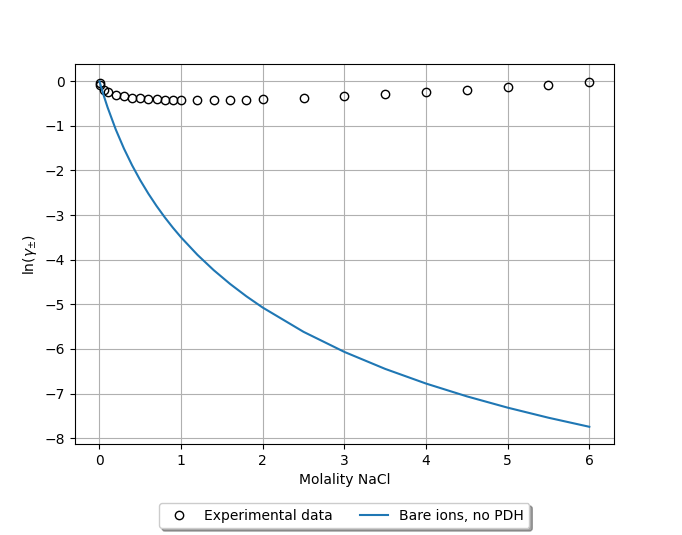
Note that converting the mole fractions to molalities (mol/kg) can be done simply with

\[m_i = \frac{x_i}{0.001 M_s(1-2*x_i)}\]

where \(M_s\) is the molar mass of the solvent (in g/mol), and \(x_i\) is the mole fraction of Na+.

(2) Using hydrated ions without the PDH correction

One of the most important effects in this system is the solvation of the dissociated ions with water molecules. Water molecules interact strongly with the Na+ and Cl- ions in solution, and in this example we will demonstrate that including explicitly solvated species captures the behavior of the system much better than standard COSMO-RS does.

First, we need to do a series of calculations to generate .coskf files for the Na+ and Cl- ions with various degrees of hydration. The geometries of these structures are shown below:

../_images/na+.png ../_images/Na+_1_H2O.png ../_images/Na+_2_H2O.png ../_images/Na+_3_H2O.png ../_images/Na+_4_H2O.png

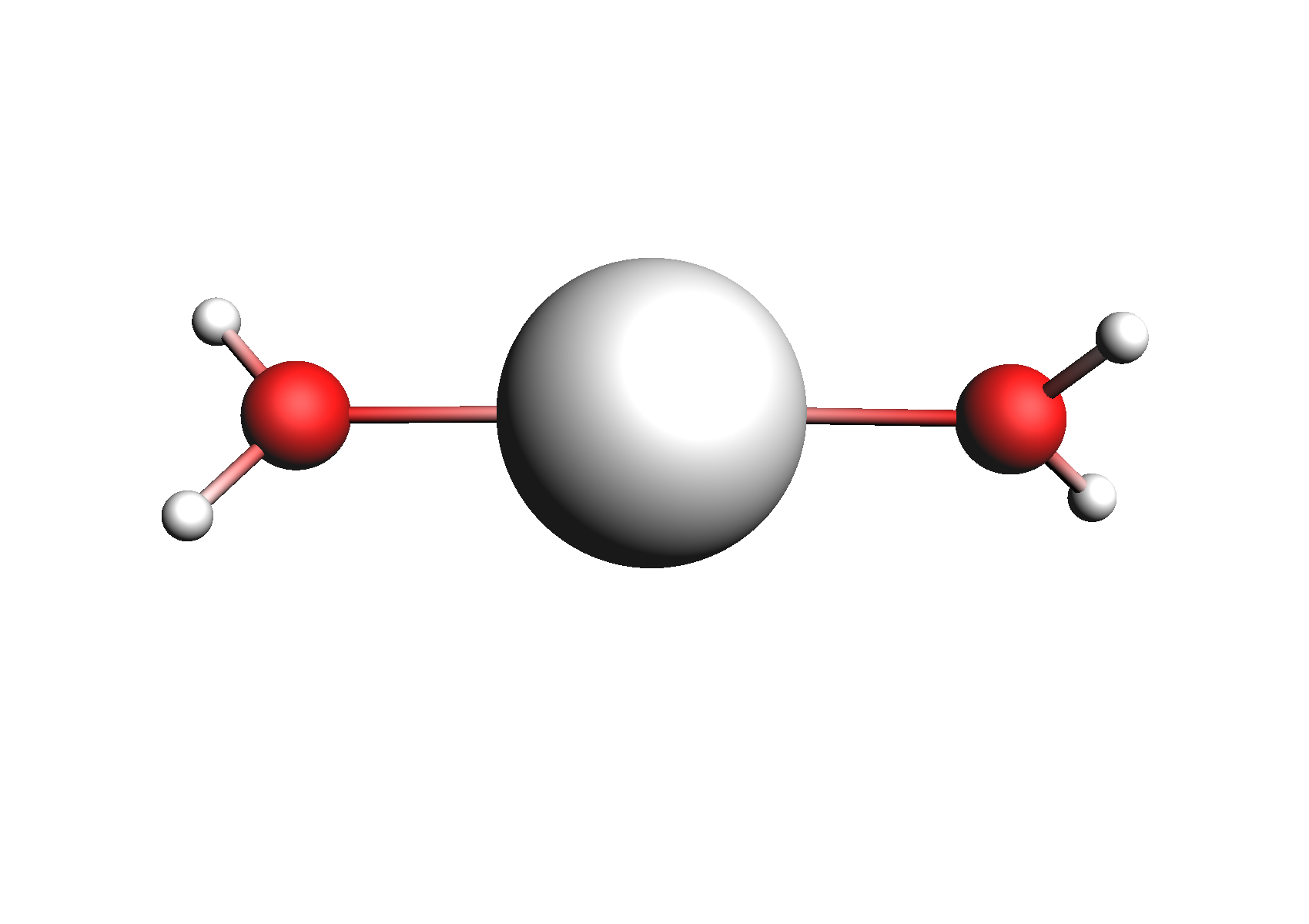
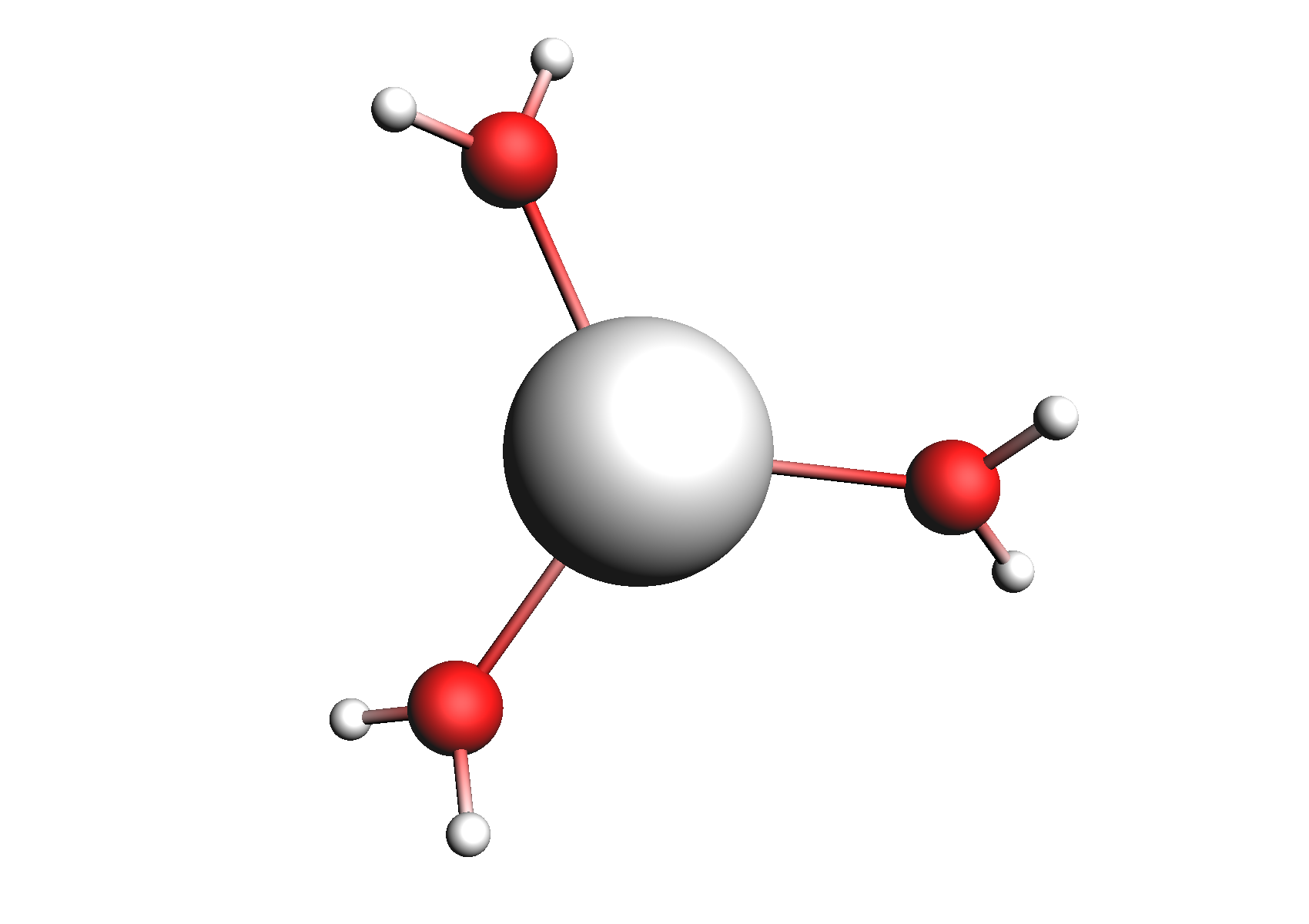
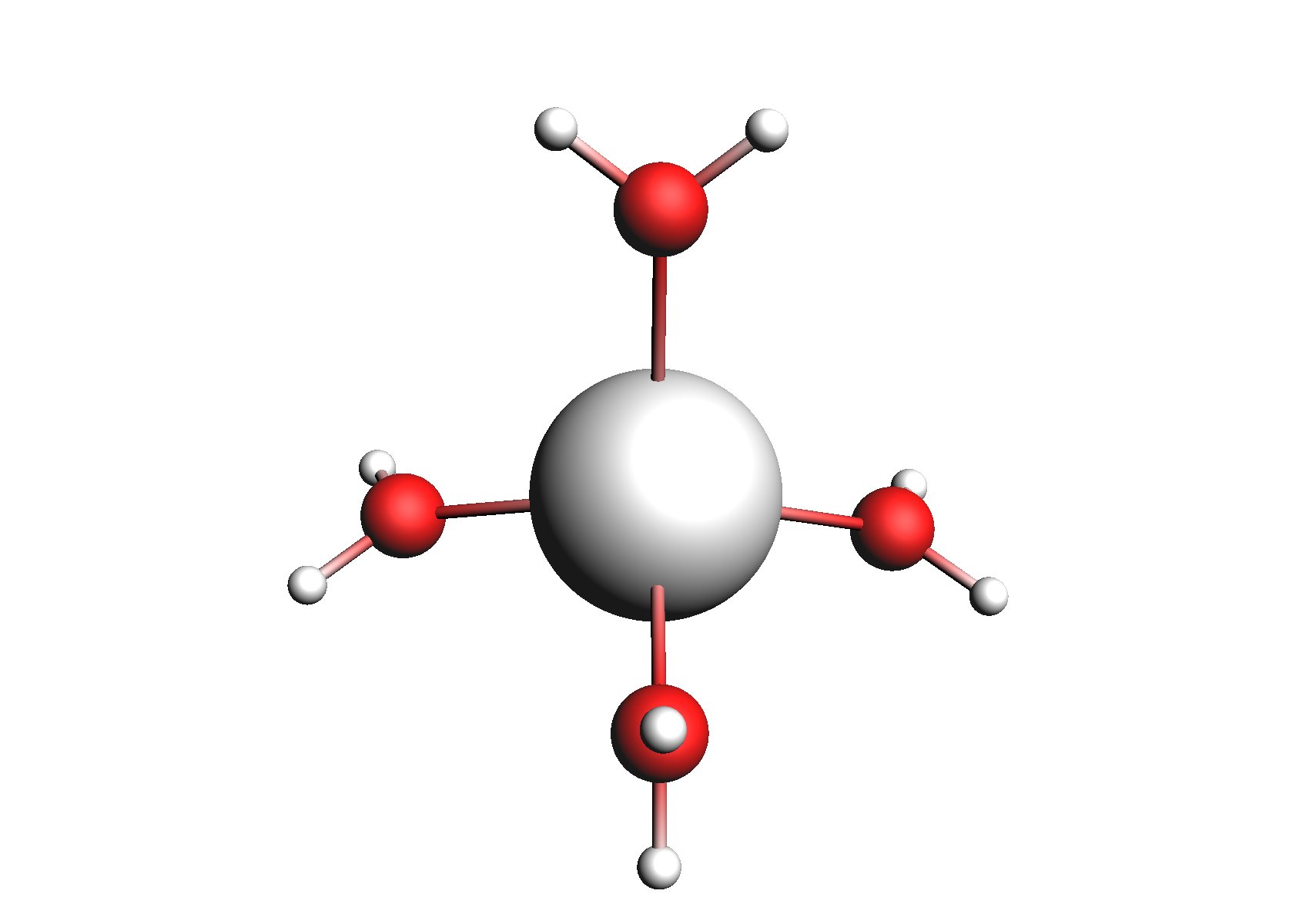
Structures used for the Na+ cation (unassociated and 1,2,3,4 explicit waters)

../_images/Cl-.png ../_images/Cl-_1_H2O.png ../_images/Cl-_2_H2O.png

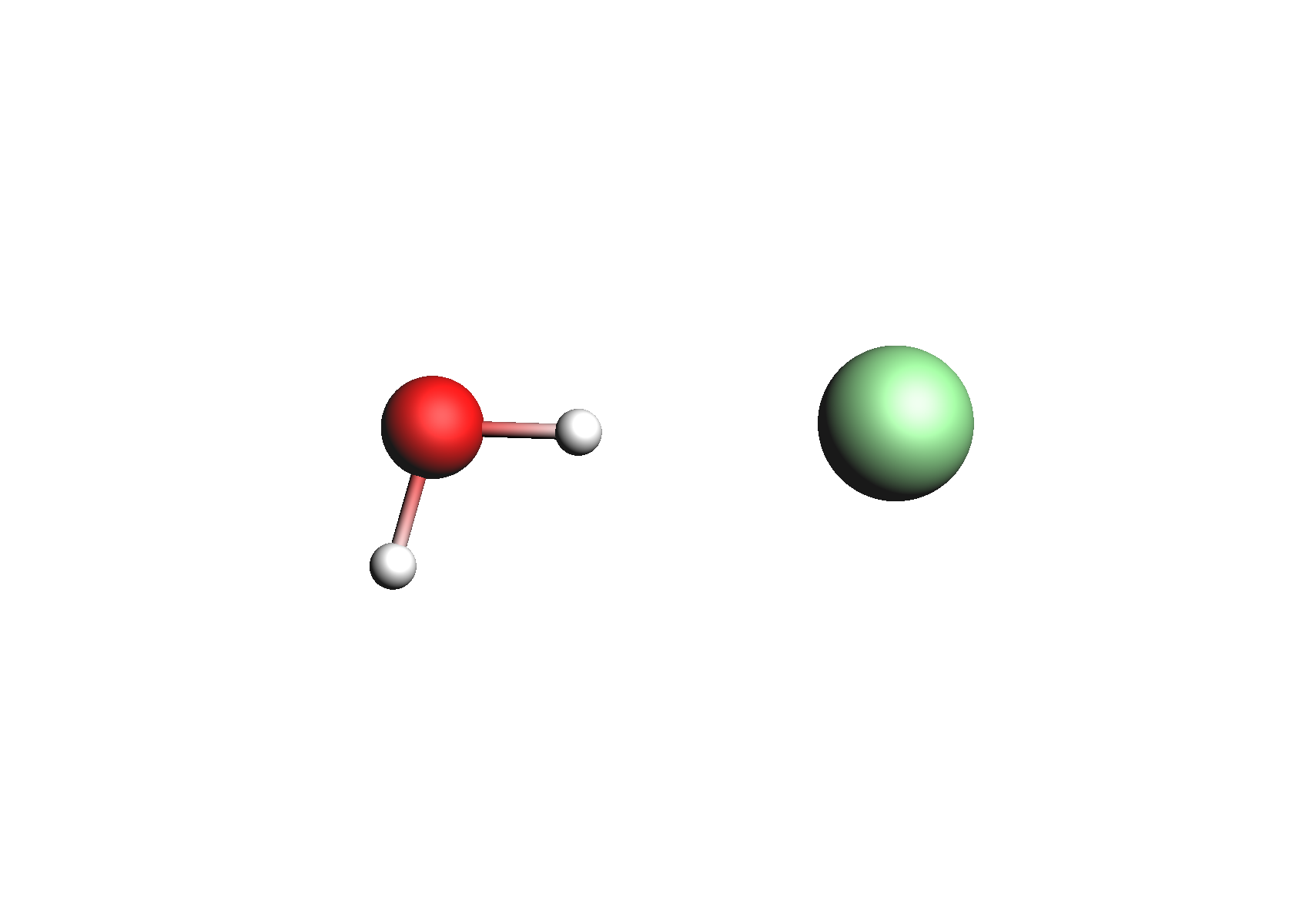
Structures used for the Cl- anion (unassociated and 1,2 explicit waters)

To consider Na+ as a species that can associate, we input the multiform version of Na+:

Compounds → List of Added Compounds
Add all of the Na+ .coskf files to the GUI with Add
Compounds → Compound with multiple forms
Hit Clear if not empty
In the conformers box, add the free Na+ ion
In the associated section at the bottom, enter the Na+(H2O) .coskf file in the topmost box below Associated
In the box below, enter Water and make sure the requires count is set to 1
Click the form a1 dropdown box and change to form a2
In the associated section at the bottom, enter the Na+(H2O)2.coskf file in the topmost box below Associated
In the box below, enter Water and make sure the requires count is set to 2
Repeat this procedure for the coskf files with 3 and 4 explicit waters
…
Click Save

This should result in the following:

../_images/na+_multiform.png

Next, we need to input the multiform Cl-:

Compounds → List of Added Compounds
Add all of the Cl- .coskf files to the GUI with Add
Compounds → Compound with multiple forms
Hit Clear if not empty
In the conformers box, add the free Cl- ion
In the associated section at the bottom, enter the Cl-(H2O) .coskf file in the topmost box below Associated
In the box below, enter Water and make sure the requires count is set to 1
Click the form a1 dropdown box and change to form a2
In the associated section at the bottom, enter the Cl-(H2O)2.coskf file in the topmost box below Associated
In the box below, enter Water and make sure the requires count is set to 2
Click Save

Finally, we run calculations with these compounds. We’ll again do a solvent composition line calculation:

Method → Parameters
In the section Correction terms, untick Use Pitzer-Debye-Hückel electrostatic correction
Properties → Solvents s1-s2 composition line
Choose 3 components
Enter the .multiform file for Na+ in the first box and set (s1,s2) to (0.1,0.0)
Enter the .multiform file for Cl- in the second box and set (s1,s2) to (0.1,0.0)
Enter the .coskf file for Water in the third box and set (s1,s2) to (0.8,1.0)
Change n to 10
Hit Run

This should result in the following:

../_images/multiform_run.png

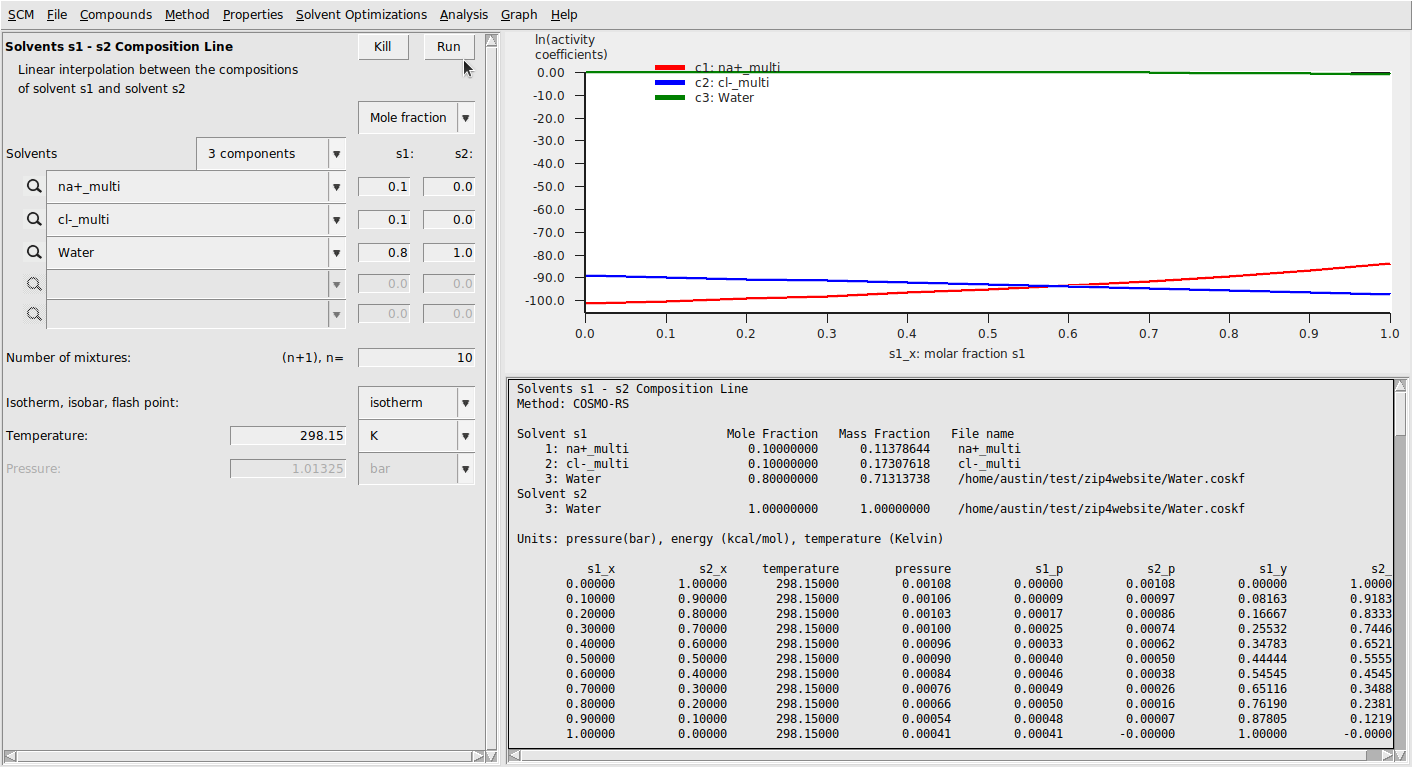
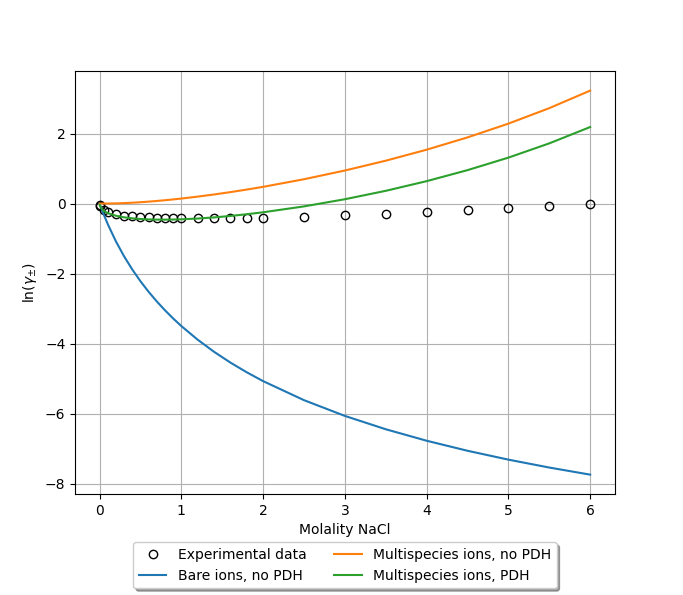
Mean ionic activity coefficients can be calculated with the exact same procedure as above. This results in a much better correspondence to experiment 2, though the results seem to show the wrong trend.

../_images/multi_ions_no_pdh.png

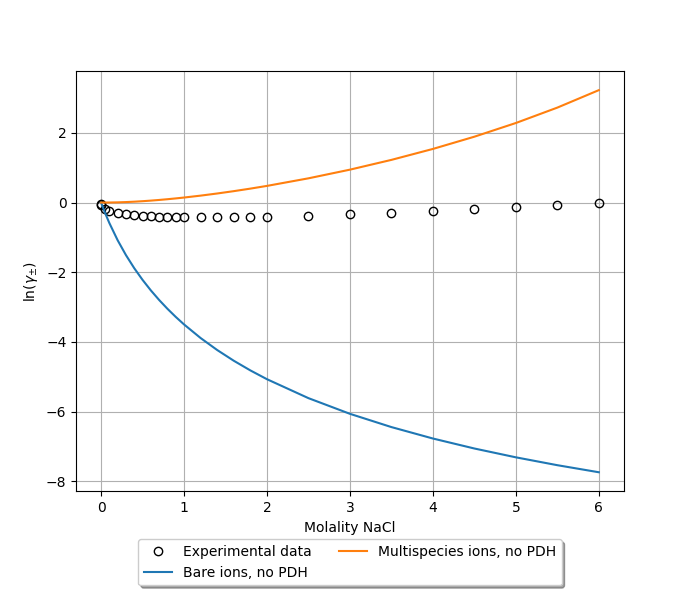
(3) Using hydrated ions with the PDH correction

Finally, we use hydrated ions in combination with the PDH correction.

Note

All calculations using the PDH corrections will require densities and dielectric constants for all compounds in the system.

Setting the density and dielectric constant can be done from the Compounds → List of added compounds menu. This input for Na+ looks like the following:

../_images/Na+_input.png

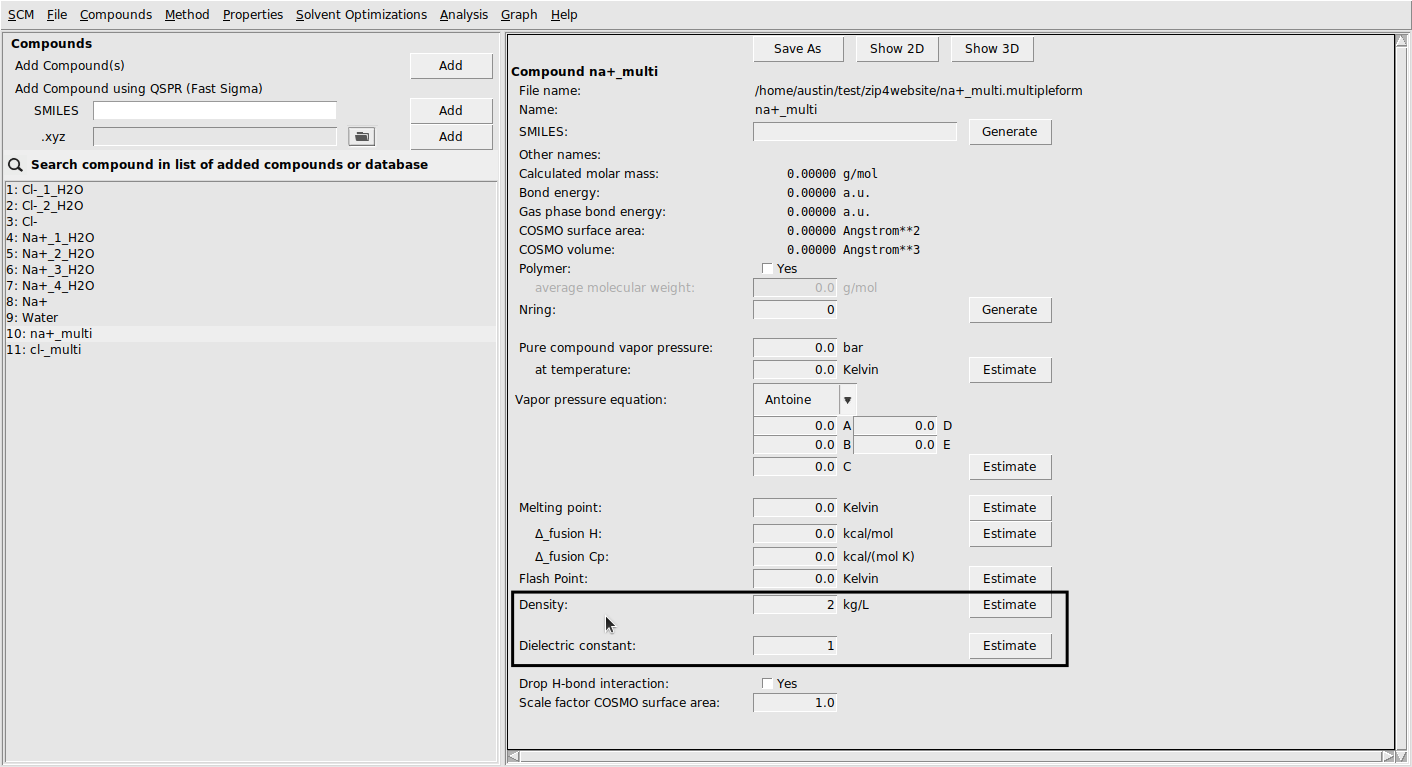
Now, use the following procedure to set up the calculation:

Method → Parameters
In the section Correction terms, tick Use Pitzer-Debye-Hückel electrostatic correction
Compounds → List of added compounds
For the Na+ multiform file, set the density to 2 kg/L and the Dielectric constant to 1
For the Cl- multiform file, set the density to 2 kg/L and the Dielectric constant to 1
For the Water coskf file, set the density to 1 kg/L and the Dielectric constant to 78
Properties → Solvents s1-s2 composition line
Choose 3 components
Enter the .multiform file for Na+ in the first box and set (s1,s2) to (0.1,0.0)
Enter the .multiform file for Cl- in the second box and set (s1,s2) to (0.1,0.0)
Enter the .coskf file for Water in the third box and set (s1,s2) to (0.8,1.0)
Change n to 10
Hit Run

Again following the procedure above to calculate molality-based mean ionic activity coefficients, we obtain a good correspondence to experiment 2, at least for small to moderate ion concentrations.

../_images/multi_ions_pdh.png

Additional comments

This tutorial provided a basic example of how to add the PDH electrostatic correction for systems with charged species. Attempting to keep the tutorial instructive and easy-to-follow, many considerations for modeling ions with COSMO-RS were left out. Some of these considerations may have improved the quantitative accuracy of this example. A few additional suggestions for modeling small ion/water systems are given below:

  • The sigma profiles of small ions are very sensitive to the atomic radii. Altering the default radii of small ions (cations in particular) may lead to better results. See 3 for an example of using non-default values for the radii.

  • Adding correct values for the Hcorr and Scorr parameters may also lead to better results. Without these parameters, the fully hydrated species (Na+ with 4 waters and Cl- with 2) are preferred across the whole concentration range. Using these parameters may lead to a more noticeable change in hydration number as a function of ion concentration

References

1

Pitzer, Kenneth S., and John M. Simonson. Thermodynamics of multicomponent, miscible, ionic systems: theory and equations. The Journal of Physical Chemistry 90 (1986): 3005-3009.

2(1,2,3)

Hamer, Walter J., and Yung‐Chi Wu. Osmotic coefficients and mean activity coefficients of uni‐univalent electrolytes in water at 25° C. Journal of Physical and Chemical Reference Data 1.4 (1972): 1047-1100.

3

Toure, Oumar, André Lebert, and Claude-Gilles Dussap. Extension of the COSMO-RS-PDHS model to the prediction of activity coefficients in concentrated water-electrolyte and water-polyol solutions. Fluid Phase Equilibria 424 (2016): 90-104.