pKa values¶

Empirical pKa calculation method¶

In Refs. [511,512] one can find several strategies to calculate pK_a values. The strategy described in this example does not take into account explicit solvent molecules, only the continuum model is included. Like in Ref. [512] an empirical fit is used to correlate calculated values with experimental pK_a values, to account for systematic errors. The largest errors are probably present in the calculation of the solvation energies of the charged species. In these cases one probably should include explicit solvent molecules, however, that may introduce other sources of errors, and this will not be investigated here. The calculation of pK_a values of acids (HA) and bases (B) is based on the following reaction model:

(acids) HA (aq, 1M) + H2O (l, 1M) → H3O⁺ (aq, 1M) + A^- (aq, 1M) (5.1.1)

(bases) HB⁺ (aq, 1M) + H2O (l, 1M) → H3O⁺ (aq, 1M) + B (aq, 1M) (5.1.2)

The free energy of dissociation for acids and bases is calculated as

(acids) \(\Delta\)G^*_diss = G(A^-) - G(HA) + G(H3O⁺) - G(H2O) (5.1.3)

(bases) \(\Delta\)G^*_diss = G(B) - G(HB⁺) + G(H3O⁺) - G(H2O) (5.1.4)

The ^* denotes a standard state of 1M (1 mol/L). The pK_a can then be calculated as (see for example Refs. [511,512])

pK_a = \(\Delta\)G^*_diss/(RT ln(10)) - 1.74 (5.1.5)

At T = 298.15, 1/(RT ln(10)) = 0.733 mol/kcal. The term -1.74 is to correct for the standard state of liquid water, which is 55 mol/L.

Emperical fit

Like in Ref. [512] instead of this equation (5.1.5), a linear fit has been made by correlating the calculated \(\Delta\)G^* _diss values with experimental pK_a values, to account for systematic errors that are present in this method. For acids and bases a different empirical adjusted equation will be used, optimized for the ADF COSMO-RS implementation:

(acids) pK_a = 0.62 \(\Delta\)G^*_diss/(RT ln(10)) + 2.10 (5.1.6)

(bases) pK_a = 0.67 \(\Delta\)G^*_diss/(RT ln(10)) - 2.00 (5.1.7)

These fitted parameters are not so far from the fitted parameters in Ref. [512]. Zero-point vibrational energies have not been taken into account in the calculation of the free energy of dissociation. H₃ O⁺ (Hydronium ion) is the conjugate acid of Water. Molecules can have two or more equivalent sites for protonation or deprotonation are also not taken into account, which can have an effect on the pK_a value. However, such effects are not taken into account here. Like for neutral compounds, one should optimize the anions and cations in the gas phase, and use this geometry also in the COSMO calculation. It is important to choose the lowest energy conformer. In the example below the molecules have a single relevant conformation for the protonated and deprotonated form.

Acids

Add the compounds in $AMSHOME/examples/COSMO-RS/pKa/tutorial5.1_acid.compoundlist using the Add compounds function in the GUI (Compounds → List of Added Compounds). The tutorial5.1_acid.compoundlist is a file with a list of acids and their conjugate bases that is limited to the compounds needed in this example. In these .coskf files already the correct number of ring atoms is included.

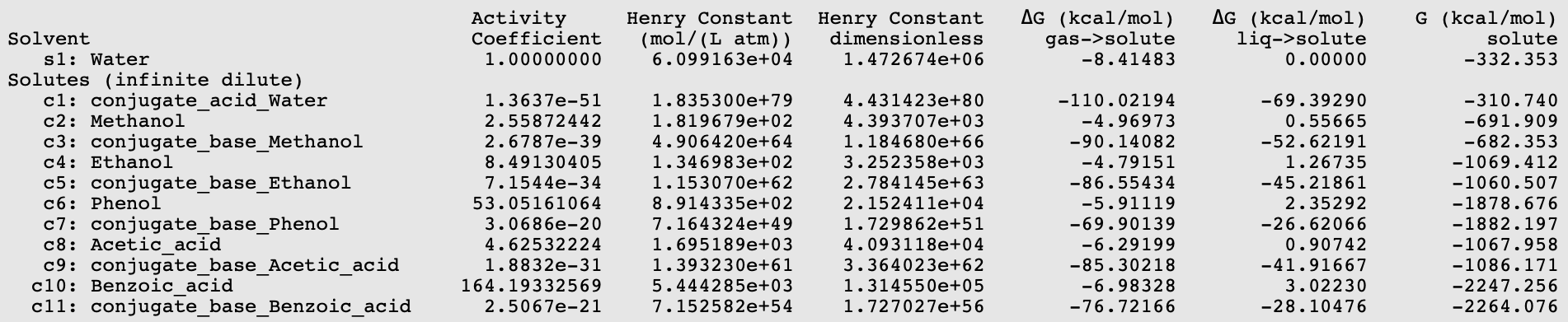
Using equation 5.1.6 (pK_a = 0.62*0.733* \(\Delta\)G_diss +2.10), with \(\Delta\)G_diss = G(conjugate_base_acid) - G(acid) + G(conjugate_acid_Water) - G(Water) in kcal/mol, results can be put in a table.

Bases

Copy the .coskf files which are listed in $AMSHOME/examples/crs/Tutorial5/tutorial5.1_base.compoundlist and the file tutorial5.1_base.compoundlist the directory Tutorial. The tutorial5.1_base.compoundlist is a file with a list of bases and their conjugate acids that is limited to the compounds needed in this example. In these .coskf files already the correct number of ring atoms is included.

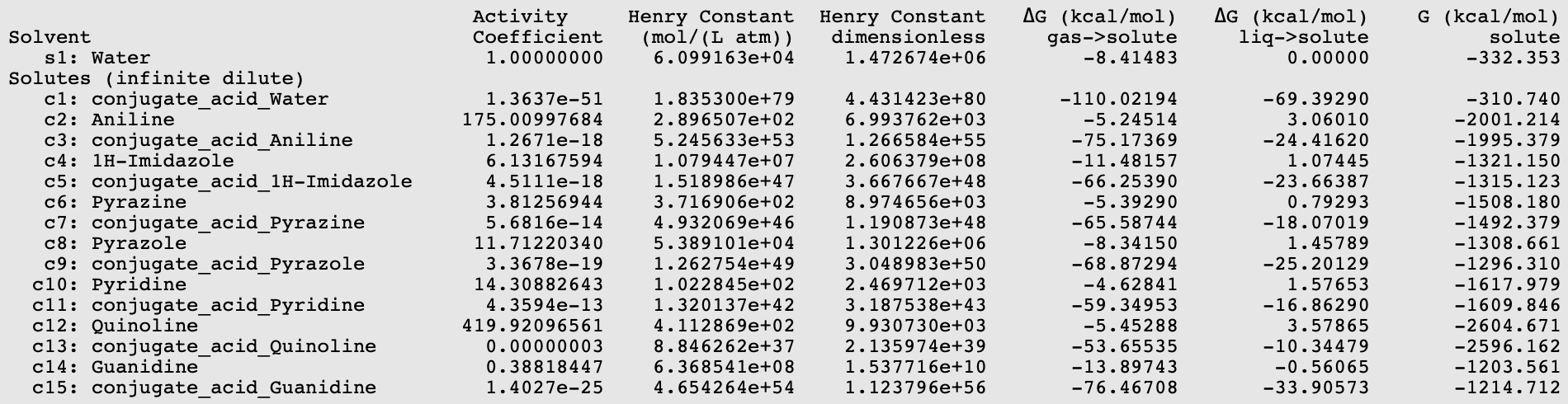
Using equation 5.1.7 ((pK_a = 0.67*0.733* \(\Delta\)G_diss -2.00), with \(\Delta\)G_diss = G(base) - G(conjugate_acid_base) + G(conjugate_acid_Water) - G(Water) in kcal/mol, results can be put in a table.

511. J. Ho and M.L. Coote, A universal approach for continuum solvent pK_a calculations: are we there yet?, Theoretical Chemistry Accounts 125, 3 (2010)

512. F. Eckert, M. Diedenhofen, and A. Klamt, Towards a first principles prediction of pK_a : COSMO-RS and the cluster-continuum approach, Molecular Physics 108, 229 (2010)

Relative pKa calculation method¶

The method described in this example is based on one of the strategies in Ref. [521]. This method uses the experimental pK_a value of a reference compound, experimental gas phase deprotonation energies, and COSMO-RS solvation free energies. A suitable reference compound (HRef) should be chosen, which is similar to the actual compound (HA) one is interested in. For example, the deprotonation reaction could be similar in both compounds. The calculation of pK_a values is based on the following reaction model:

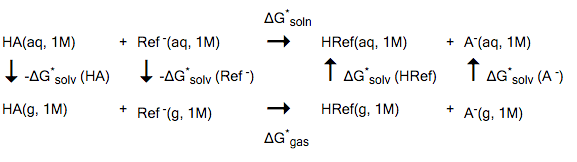
The ^* denotes a standard state of 1M (1 mol/L). The free energy of solvation is then calculated as

\(\Delta\)G^* _soln = \(\Delta\)G^* _gas + \(\Delta\)G^* _solv (HRef) + \(\Delta\)G^* _solv (A^- ) - \(\Delta\)G^* _solv (HA) - \(\Delta\)G^* _solv (Ref^- )

The pK_a can then be calculated as (see for example Ref. [521])

pK_a = \(\Delta\)G^* _soln /(RT ln(10)) + pK_a (HRef)

The success of this method relies on the availability of a suitable reference compound with an accurately known experimental pK_a value. Instead of experimental gas phase deprotonation energies one might calculate the gas phase reaction free energy \(\Delta\)G^* _gas , using DFT or some high level ab initio method.

Example Ethanol

In this example the pK_a value of Ethanol will be calculated. As reference compound Methanol is chosen, which has an experimental pK_a value of 15.5. Experimental deprotonation energies are taken from Ref. [521, supporting information], for Methanol this is \(\Delta\)_r G⁰ = 1569 kJ/mol, and for Ethanol \(\Delta\)_r G⁰ = 1555 kJ/mol, see also, for example, Ref. [522]. The COSMO-RS solvation free energies, \(\Delta\text{G(gas->solute)}\), of Methanol, Methoxide (the conjugate base of Methanol), Ethanol, and Ethoxide (the conjugate base of Ethanol) have already been calculated in the previous tutorial 5.1. At T = 298.15, 1/(RT ln(10)) = 0.733 mol/kcal. The free energy of solvation (kcal/mol) and the pK_a of Ethanol are then calculated as

\(\Delta\)G^* _soln = (1555-1569)/4.184 - 4.97 - 86.56 + 4.79 + 90.14 = 0.05 kcal/mol

pK_a (Ethanol) = 0.733*0.05 + 15.5 \(\approx\) 15.5

The calculated pK_a of Ethanol of 15.5 is close to the experimental value of 15.9.

521. J. Ho and M.L. Coote, A universal approach for continuum solvent pK_a calculations: are we there yet?, Theoretical Chemistry Accounts 125, 3 (2010)

522. NIST Chemistry WebBook