Energy Decomposition Analysis (EDA)

Energy Decomposition Analysis of Ammonia Borane

This tutorial explains how to perform an energy decomposition analysis (EDA) [1] of Ammonia borane, in which ammonia and borane have a donor-acceptor interaction with each other. Hereby, the user can examine which interactions result in a stable complex.

The bond energy of H₃N-BH₃ is defined as:

\[\Delta E = E_{NH_3-BH_3} - E_{NH_3} -E_{BH_3}\]

in which E_NH3 and E_BH3 are the energies of the optimized reactants, and E_H3N-BH3 is the energy of the optimized complex. The bond energy consists of the preparation energy, also known as the strain energy, and the interaction energy:

\[\Delta E = \Delta E_{prep} + \Delta E_{int}\]

The preparation energy is the amount of energy that is required to deform the NH₃ and BH₃ from their equilibrium structure to the geometry they have in the complex. The interaction energy is the change in energy when the prepared fragments (NH₃ and BH₃ in the complex geometry) are combined to form the complex. A quantitative energy decomposition analysis (EDA) divides the interaction energy in the electrostatic interaction, Pauli repulsion, and attractive orbital interactions:

\[\Delta E_{int} = \Delta V_{elstat} + \Delta E_{Pauli} + \Delta E_{oi}\]

The electrostatic interaction, which is usually attractive, is the energy between the unperturbed charge distributions of the prepared fragments. The Pauli repulsion is responsible for steric repulsion, it consists of the destablilizing interactions between occupied orbitals of the fragments. The orbital interaction accounts for charge transfer and polarization.

If you want to do an EDA with unrestricted fragments, see the following tutorial instead.

Geometry Optimization

The geometry of the reactants and the product (complex) must be optimized. Note that another basis set and functional can be used as well. Symmetry will be used, which may help in the analysis.

Perform the following steps for NH₃, BH₃ and H₃N-BH₃:

1. In AMSinput build the structure (or search for it in the search box )

2. Symmetrize the system by clicking on

3. Select Task → Geometry Optimization

4. Select XC functional → GGA:BP86

5. Select Basis set → TZP

5. Select Numerical quality → Good

7. Run the calculation with File → Run (give an appropriate name to your calculations)

8. When the run has finished, click ‘Yes’ to import the optimized coordinates and save it

The bond energy of H₃N-BH₃ can be calculated by subtracting the energies of the reactants, NH₃ and BH₃ from the energy of the complex. The energies can be found at the bottom of the logfile or in the output.

\[\Delta E = E_{H_3N-BH_3} - E_{NH_3} -E_{BH_3}\]

The bond energy of H₃N-BH₃ was calculated to be -31.80 kcal/mol with these settings. (-838.47 - (-444.53) - (-362.14) = -31.80)

EDA

Single point calculations of the prepared fragments NH₃ and BH₃ are needed to perform an EDA. In the GUI, single points of the fragments will be computed automatically when you follow the next steps for a fragment analysis:

Perform a new calculation using the geometry of the optimized complex (H₃N-BH₃):

1. Select Task → Single Point

2. Select XC functional → GGA:BP86

3. Select Basis set → TZP

4. Select Numerical quality → Good

5. Go in the panel bar to Model → Regions

6. Select the atoms of NH₃ and click the button next to Regions

7. Select the atoms of BH₃ and click also on the button

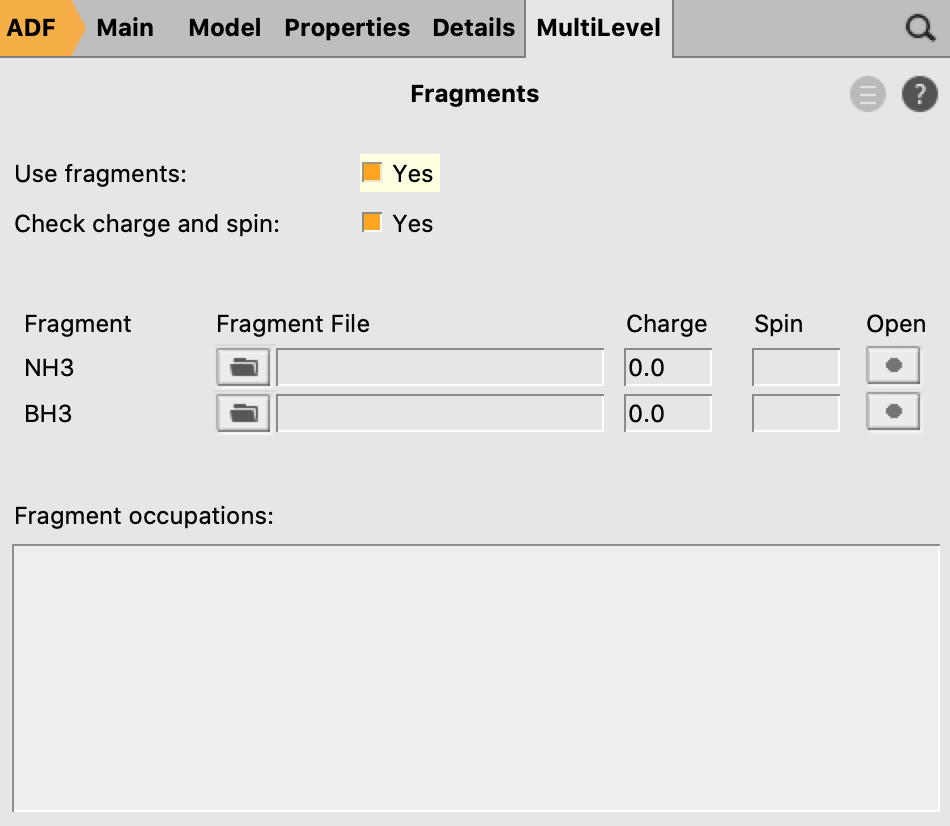
8. Go in the panel bar to MultiLevel → Fragments

9. Check the ‘Use fragments’ check box

10. Run the calculation

When doing calculations on a cluster, single point calculations of NH₃ and BH₃ in their prepared geometry must be performed at first. The adf.rkf files of the single point computations are needed for the fragment analyses.

Analysis

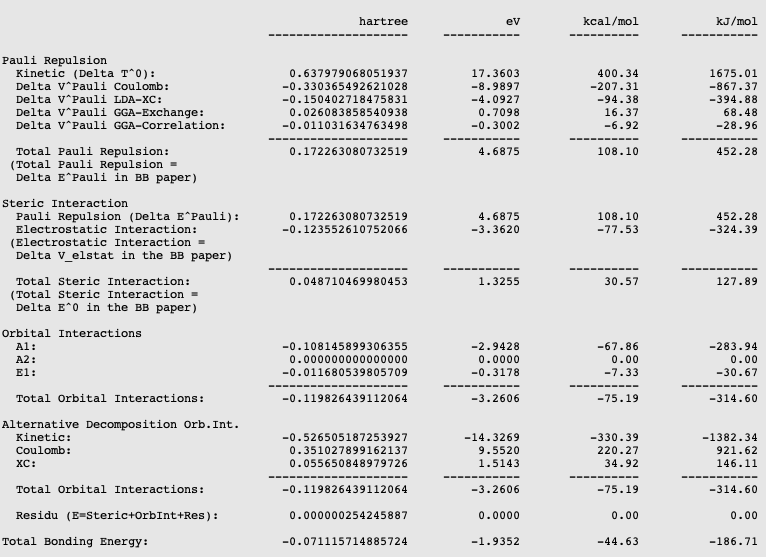
The energy decomposition of the interaction energy of H₃N-BH₃ can be found in the output file of the fragment analysis. You can find for instance that H₃N-BH₃ has an interaction energy of -44.63 kcal/mol, which consists of a Pauli repulsion of 108.10 kcal/mol, an electrostatic interaction of -77.53 kcal/mol, and an orbital interaction of -75.19 kcal/mol. This results in an interaction energy of -44.63 kcal/mol.

The orbital interaction is decomposed into contributions from different irreducible representations of the molecular point group. In this case the contributions from A1 (\(\sigma, \sigma^*\)-orbitals) are much more important than those from E1 (\(\pi, \pi^*\)-orbitals).

The bond energy was calculated previously to be -31.80 kcal/mol and accordingly the preparation energy can be calculated to be 12.83 kcal/mol (=-31.80-(-44.63)). The structure of the fully relaxed NH₃ is only slightly different from the structure of the NH₃ fragment in H₃N-BH₃. However, the structure of the fully relaxed flat BH₃ (symmetry D_3h) is substantially different than the structure of the BH₃ trigonal pyramidal fragment in H₃N-BH₃ (symmetry C_3v):

The preparation energy for NH₃ is only 0.11 kcal/mol, the difference between the bond energy of the NH₃ fragment (-444.42 kcal/mol) and the fully relaxed NH₃ molecule (-444.53 kcal/mol). Due to the relatively large structural changes the preparation energy for BH₃ is much larger, namely 12.72 kcal/mol, the difference between the bond energy of the BH₃ trigonal pyramidal fragment (-349.42 kcal/mol) and the fully relaxed planar BH₃ molecule (-362.14 kcal/mol). Note that the energies of the fragments can be found at the bottom of the logfile or in the output of the fragments.

With AMSlevels the molecular orbital diagram can be visualized, in which one can see a donor-acceptor interaction and (repulsive) interactions between occupied orbitals.

1. SCM → Levels

2. In AMSlevels, click on View → Labels → Show

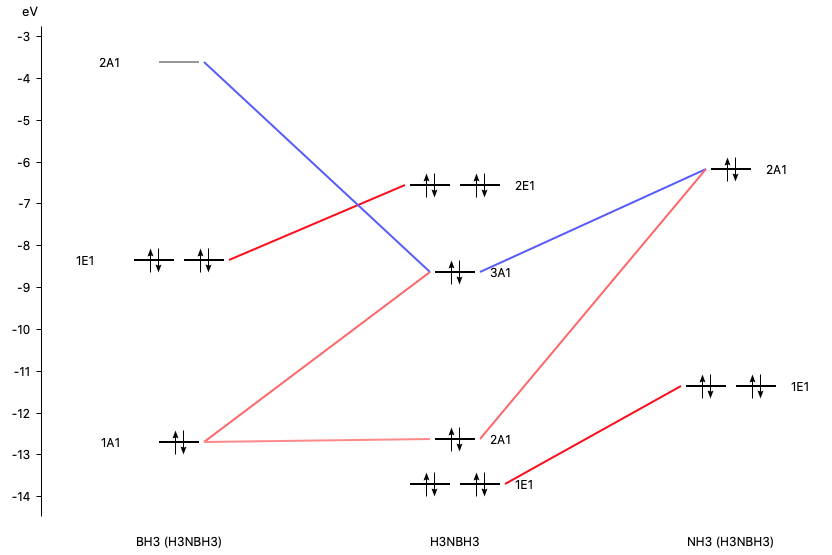
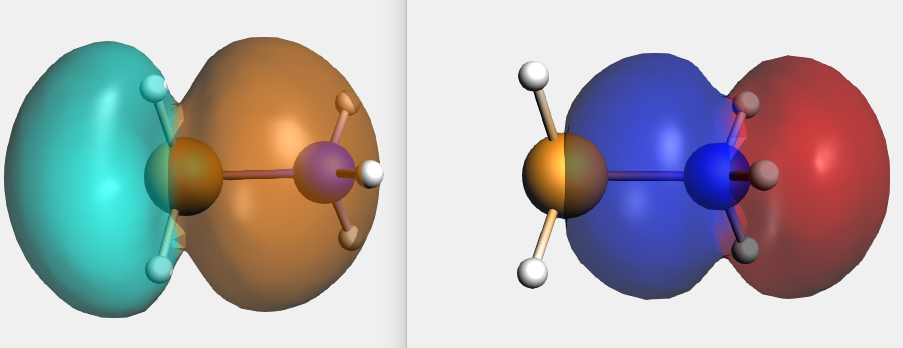
By right clicking the BH₃ 2A1 fragment orbital (LUMO of BH₃, acceptor orbital) one can select the corresponding SFO (fragment orbital), which can be visualized with AMSview. Similar one can select the NH₃ 2A1 fragment orbital (HOMO of NH₃, donor orbital). After some manipulations, using 50% opacity, one can get the following two AMSview windows that show these fragment orbitals.

EDA with unrestricted fragments

This tutorial explains how to perform an energy decomposition analysis (EDA) of a molecule with unrestricted fragments, for example the CH₃ groups of ethane. Hereby, the user can examine which interactions result in the stable molecule. To see an explanation of these different interactions or to do an EDA without unrestricted fragments, see the EDA of Ammonia Borane tutorial.

Geometry Optimization

The geometry of the reactants and the product (complex) must be optimized. Note that another basis set and functional can be used as well. . Symmetry will be used, which may help in the analysis.

For ethane:

1. In AMSinput make the structure or search for the structure in the search box in the panel bar

2. Symmetrize the system by clicking on

3. Select Task → Geometry Optimization

4. Select XC functional → GGA:BP86

5. Select Basis set → TZP

5. Select Numerical quality → Good

7. Run the calculation with File → Run (give an appropriate name to your calculations)

8. When the run has finished, click ‘Yes’ to import the optimized coordinates and save it

For CH₃ (methyl) an unrestricted calculation is needed:

1. In AMSinput make the structure or search for the structure in the search box in the panel bar

2. Symmetrize the system by clicking on

3. Select Task → Geometry Optimization

4. Check the Unrestricted box.

5. Enter 1.0 as Spin polarization

6. Select XC functional → GGA:BP86

7. Select Basis set → TZP

8. Select Numerical quality → Good

9. Run the calculation with File → Run (give an appropriate name to your calculations)

10. When the run has finished, click ‘Yes’ to import the optimized coordinates and save it

The bond energy of C₂H₆ can be calculated by subtracting the energies of the reactants (two CH₃) from the energy of the complex. The energies can be found at the bottom of the logfile or in the output.

\[\Delta E = E_{C_2H_6} - 2 E_{CH_3}\]

The bond energy of C₂H₆ was calculated to be -93.53 kcal/mol with these settings. (-920.23 - 2*(-413.35)) = -93.53)

EDA

Single point calculations of the CH₃ groups in the geometry they have in the product are needed to perform an EDA. Note that one sometimes need to change the electron configuration of the fragments to make them so called ‘prepared for bonding’ in order to minimize the Pauli repulsion in the electron pair bond. This is not needed in this simple example.

1. Perform a new calculation with the optimized molecule, ethane

2. Select the Task Single Point

3. Check the Unrestricted box.

4. Select XC functional → GGA:BP86

5. Select Basis set → TZP

6. Select Numerical quality → Good

7. Go in the panel bar to Model → Regions

8. Select the atoms of one CH₃ group and click the button next to Regions

9. Select the atoms of the other CH₃ group and click also on the button

10. Go in the panel bar to MultiLevel → Fragments

11. Check the ‘Use fragments’ check box (A warning will popup regarding NOSYM symmetry)

12. Enter as spin 1 for one of the fragments and -1 for the other fragment

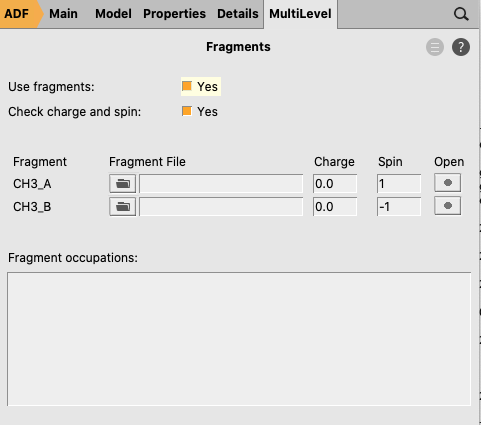
The symmetry has been adjusted to NOSYM. However, we want to use symmetry. Besides setting the symmetry to AUTO, in this case we also need to symmetrize the coordinates again, since using fragments will lower the symmetry of ethane that ADF can use from D_3d to C_3v. Note that in this case the symmetrization will only reorient the geometry in order to fulfill the molecular orientation requirements in ADF such that ADF can use symmetry.

13. Go in the panel bar to Details → Symmetry

14. Select Symmetry → AUTO

15. Symmetrize the system by clicking on

16. Save it and run the calculation

Analysis

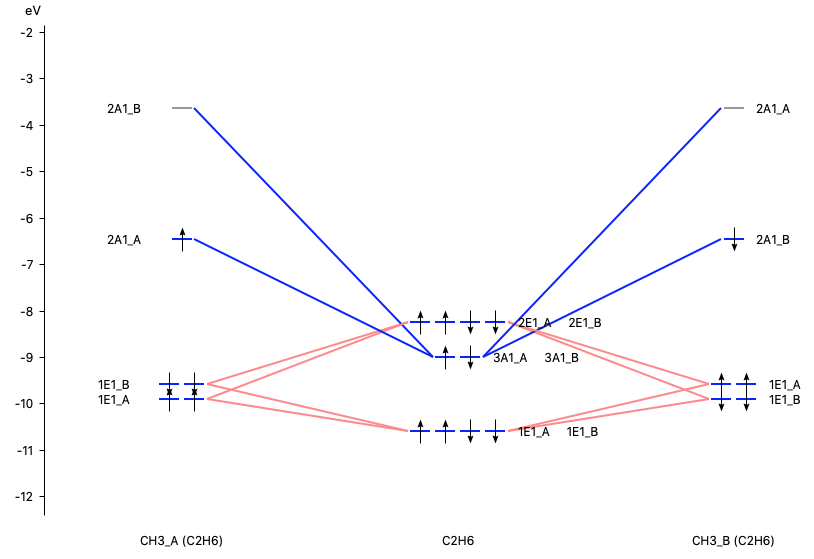
The different energies, where the interaction energy of the CH₃ groups of ethane consists of, are noted in the output. It can be noticed that the interaction energy of -111.41 kcal/mol is build out of 180.02 kcal/mol Pauli repulsion, -125.43 kcal/mol electrostatic interaction, and -166.02 kcal/mol orbital interactions.

The orbital interaction is decomposed into contributions from different irreducible representations of the molecular point group. In this case the contributions from A1 (\(\sigma, \sigma^*\)-orbitals) are much more important than those from E1 (\(\pi, \pi^*\)-orbitals).

The bond energy was calculated previously to be -93.53 kcal/mol and accordingly the preparation energy can be calculated to be 17.88 kcal/mol (=-93.53-(-111.41)). The preparation energy for one CH₃ fragment is 8.95 kcal/mol, the difference between the bond energy of the CH₃ trigonal pyramidal fragment (-404.40 kcal/mol) and the fully relaxed planar CH₃ molecule (-413.35 kcal/mol). The preparation energy of the other CH₃ fragment is the same. Note that the energies of the fragments can be found at the bottom of the logfile or in the output of the fragments.

With AMSlevels the molecular orbital diagram can be visualized, in which one can see an electron-pair bond and (repulsive) interactions between occupied levels.

[1]	F.M. Bickelhaupt, E.J. Baerends J.P., Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry, Reviews in Computational Chemistry 15, 1 (2000)