Input, execution and output¶
Input¶
The input for AMS has a block and keyword structure. See the General remarks on input structure and parsing section for more details.
The input keys System, Task, and Engine, are obligatory. Most other input keys in AMS are optional, like Properties. In the rest of this manual one can find all input keys for AMS.
The Engine specific input can be found in the respective Engine Manuals, for example, the manual for ADF, BAND, DFTB, ForceField, MOPAC, and ReaxFF.
Example¶
The AMS input has a special Engine block, that selects which engine is used for
the simulation and also contains all the details of its configuration. This is
probably best illustrated by an example. Let us look at the following AMS
input, which optimizes the geometry of the methane molecule and calculates its
normal modes of vibration at the optimized geometry:
$AMSBIN/ams << EOF
Task GeometryOptimization
GeometryOptimization
Convergence
Gradients 1.0e-4
End
End
Properties
NormalModes true
End
System
Atoms
C 0.00000000 0.00000000 0.00000000
H 0.63294000 -0.63294000 -0.63294000
H -0.63294000 0.63294000 -0.63294000
H 0.63294000 0.63294000 0.63294000
H -0.63294000 -0.63294000 0.63294000
End
End
Engine DFTB
Model DFTB3
ResourcesDir DFTB.org/3ob-3-1
EndEngine
EOF
Note how DFTB is selected as the engine in the Engine DFTB line that opens
the Engine block. All DFTB specific configuration is contained within this
engine block, which is terminated by EndEngine. The fact that we want to run
a geometry optimization with normal modes for methane and things like
convergence criteria for the optimization are of course completely independent
from which engine is actually used to perform this calculation. Therefore they
are all found outside of the Engine block. In this sense, the AMS input is
split up into the driver level input (everything outside of the engine block)
and the engine input, which is just a single Engine block. This separation
makes it easy to perform the same calculation at a different level of theory, by
simply switching out the Engine block in the input. We could, for example,
repeat the same calculation at the DFT-GGA level using the Band engine:
Engine BAND
XC
GGA PBE
End
EndEngine
Engines like ADF or BAND that have many options and can calculate many properties,
consequently also have a large number of possible keywords in their input. In
order to have a better structured documentation we have split off the description
of the engine inputs into separate engine specific manuals,
while this AMS manual only documents the driver level keywords outside of the
Engine block. All the engine specific options are found in the respective
engine’s manual, which documents the keywords in its Engine block. In
general all engines can be used with all tasks in AMS. There are only a few
rather obvious restrictions, for example that only engines which can handle
periodic systems can be used for the calculation of phonons.
Tasks¶
The key Task is described in more detail in the section Structure, Reactivity, and Molecular Dynamics.
The Task VibrationalAnalysis is described in more detail in the section Vibrational Spectroscopy
(Mode Scanning, Mode Refinement, Mode Tracking, VG-FC Resonance Raman)
and in the section Vibrationally resolved electronic spectra
(VG-FC: Vertical Gradient Franck-Condon).
Below the possible arguments for Task are given.
Task [GCMC | GeometryOptimization | IRC | MolecularDynamics | NEB | PESExploration | PESScan |
Replay | SinglePoint | TransitionStateSearch | VibrationalAnalysis]
Properties¶
The block key Properties is described in more detail in the section Gradients, Hessian, Stress tensor, Elasticity,
in the section Vibrational Spectroscopy,
and in the section Dipole moment, Polarizability, Bond orders.
Below the possible Properties are summarized.
Properties
BondOrders Yes/No
Charges Yes/No
DipoleGradients Yes/No
DipoleMoment Yes/No
ElasticTensor Yes/No
GSES Yes/No
Gradients Yes/No
Hessian Yes/No
Molecules Yes/No
NormalModes Yes/No
OrbitalsInfo Yes/No
Other Yes/No
PESPointCharacter Yes/No
Phonons Yes/No
Polarizability Yes/No
Raman Yes/No
SelectedRegionForHessian string
StressTensor Yes/No
VCD Yes/No
VROA Yes/No
End
General remarks on input structure and parsing¶
Most keys are optionals. Defaults values will be used for keys that are not specified in the input
Keys/blocks can either be unique (i.e. they can appear in the input only once) or non-unique. (i.e. they can appear multiple times in the input)
The order in which keys or blocks are specified in the input does not matter. Possible exceptions to this rule are a) the content of non-standard blocks b) some non-unique keys/blocks)
Comments in the input file start with one of the following characters:
#,!,:::# this is a comment ! this is also a comment :: yet another comment
Empty lines are ignored
The input parsing is case insensitive (except for string values):
# this: UseSymmetry false # is equivalent to this: USESYMMETRY FALSE
Indentation does not matter and multiple spaces are treaded as a single space (except for string values):
# this: UseSymmetry false # is equivalent to this: UseSymmetry false
Environment variables in the input will be replaced by their value. We only support simple substitution of variables (optionally surrounded by
{}). All other parameter expansion features of the POSIX shell (e.g. default values) are not supported. Expansion of a variable can be prevented by prefixing the leading dollar ($) with a backslash (\). Note that variables which are not set will expand to an empty string, just like in a shell:File $SOME_DIRECTORY/file.txt File ${SOME_DIRECTORY}_BACKUP/file.txt Key \$WILL_NOT_EXPAND
Keys¶
Key-value pairs have the following structure:
KeyName Value
Possible types of keys:
- bool key
The value is a single Boolean (logical) value. The value can be
True(equivalentlyYes) orFalse(equivalentlyNo.). Not specifying any value is equivalent to specifyingTrue. Example:KeyName Yes
- integer key
The value is a single integer number. Example:
KeyName 3
- float key
The value is a single float number. For scientific notation, the E-notation is used (e.g. \(-2.5 \times 10^{-3}\) can be expressed as
-2.5E-3). The decimal separator should be a dot (.), and not a comma (,). Example:KeyName -2.5E-3
Note that fractions (of integers) can also be used:
KeyName 1/3 (equivalent to: 0.33333333333...)
- string key
The value is a string, which can include white spaces. Only ASCII characters are allowed. Example:
KeyName Lorem ipsum dolor sit amet
- multiple_choice key
The value should be a single word among the list options for that key (the options are listed in the documentation of the key). Example:
KeyName SomeOption
- integer_list key
The value is list of integer numbers. Example:
KeyName 1 6 0 9 -10
Note that one can also specify ranges of integers by specifying the interval and (optionally) the step size separated by colons:
KeyName 1:5 (equivalent to: 1 2 3 4 5) KeyName 2:10:2 (equivalent to: 2 4 6 8 10) KeyName 20:10:-2 (equivalent to: 20 18 16 14 12 10)
Note also that ranges can be freely combined with individual numbers:
KeyName 1:5 10 20 (equivalent to: 1 2 3 4 5 10 20)
- float_list key
The value is list of float numbers. The convention for float numbers is the same as for Float keys. Example:
KeyName 0.1 1.0E-2 1.3
Float lists can also be specified as a range with equidistant points, by specifying the interval’s boundaries (inclusive) as well as the number of desired subintervals separated by colons:
KeyName 1.0:1.5:5 (equivalent to: 1.0 1.1 1.2 1.3 1.4 1.5)
Range specifications can be freely combined with each other and single numbers:
KeyName 0.0 1.0:1.5:5 2.0:3.0:10
Blocks¶
Blocks give a hierarchical structure to the input, grouping together related keys (and possibly sub-blocks). In the input, blocks generally span multiple lines, and have the following structure:
BlockName
KeyName1 value1
KeyName2 value2
...
End
Headers
For some blocks it is possible (or necessary) to specify a header next to the block name:
BlockName someHeader
KeyName1 value1
KeyName2 value2
...
End
Compact notation
It is possible to specify multiple key-value pairs of a block on a single line using the following notation:
# This:
BlockName KeyName1=value1 KeyName2=value2
# is equivalent to this:
BlockName
KeyName1 value1
KeyName2 value2
End
Notes on compact notation:
The compact notation cannot be used for blocks with headers.
Spaces (blanks) between the key, the equal sign and the value are ignored. However, if a value itself needs to contain spaces (e.g. because it is a list, or a number followed by a unit), the entire value must be put in either single or double quotes:
# This is OK: BlockName Key1=value Key2 = "5.6 [eV]" Key3='5 7 3 2' # ... and equivalent to: BlockName Key1 value Key2 5.6 [eV] Key3 5 7 3 2 End # This is NOT OK: BlockName Key1=value Key2 = 5.6 [eV] Key3=5 7 3 2
Non-standard Blocks
A special type of block is the non-standard block. These blocks are used for parts of the input that do not follow the usual key-value paradigm.
A notable example of a non-standard block is the Atoms block (in which the atomic coordinates and atom types are defined).
Including an external file¶
You can include an external ASCII file in the input with the @include
directive:
@include FileName.in
@include "file name with spaces.in"
The file name should include the path, either absolute or relative to the
run-directory. The content of the file is included in the input at the point
where the @include directive occurs. The @include directive may occur
any number of times in the input.
The @include feature makes it easy to pack your preferred settings in one
file and use them in every run with minimum input-typing effort.
Units¶
Some keys have a default unit associated (not all keys have units). For such keys, the default unit is mentioned in the key documentation. One can specify a different unit within square brackets at the end of the line:
KeyName value [unit]
For example, assuming the key EnergyThreshold has as default unit hartree, then the following definitions are equivalent:
# Use defaults unit:
EnergyThreshold 1.0
# use eV as unit:
EnergyThreshold 27.211 [eV]
# use kcal/mol as unit:
EnergyThreshold 627.5 [kcal/mol]
# hartree is the atomic unit of energy:
EnergyThreshold 1.0 [hartree]
Available units:
Energy:
hartree,joule,eV,kJ/mol,kcal/mol,cm1,MHzForces:
hartree/bohr,eV/bohr,hartree/angstrom,eV/angstrom,kcal/mol/angstrom,kJ/mol/angstromLength:
bohr,angstrom,meterAngles:
radian,degreeMass:
el,proton,atomic,kgPressure:
atm,pascal,GPa,a.u.,bar,kbarElectric field:
V/angstrom,V/meter,a.u.
Execution¶
Shell script¶
The AMS driver reads its input from standard input, i.e. what is called
STDIN on Unix-like systems. Technically it is possible to run AMS and type
the input file in interactively. This is however highly impractical and most
people run AMS from a small shell script that contains the AMS text input and
sends it directly to the AMS executable.
For example, the content of the file ‘example.run’ could be like:
#!/bin/sh
$AMSBIN/ams << EOF
... AMS text input goes here:
Block
Keywork value
OtherKeyword value
End
EOF
The shell script ‘example.run’ needs be executable, if it isn’t you will need to make it executable, e.g. chmod u+x example.run.
The ‘example.run’ file needs to be executed as a shell script, not as input to AMS.
./example.run > example.out
Interactive input file¶
As of the 2021.1 version the AMS driver has the concept of an interactive input file.
The interactive input file is a second input file, that users may create in the results directory of an already running job to interact with it.
The name of the interactive input file is interactive.in.
Note that the file does not exist by default, but has to be created by the user wanting to interact with the running AMS job.
In AMS2021.1 the interactive input file may be used to request the graceful and orderly termination of a job.
echo "Stop" > ams.results/interactive.in
Stop- Type
Bool
- Default value
No
- Description
Makes the AMS driver stop execution in an ordered manner at the next opportunity. This will not interrupt the execution in the middle of the numerical calculation of a PES point property (e.g. a Hessian).
It is generally preferably to request the termination through the interactive input file over killing a job at the operating system level. This makes sure that the job stops at a logical point and still has time to write intermediate results to disk, making restarting from such jobs easier and more reliable. From the graphical user interface, the stopping can be requested in AMSjobs by selecting the running job and clicking Job → Request Early Stop in the menu bar.
As of AMS2021.1, the tasks that can be stopped through the interactive input file are:
Molecular dynamics simulations will stop at the next sampling or checkpoint as if the maximum number of steps had been reached.
Geometry optimizations will stop after the current iteration and be considered converged. This can be used if a geometry optimization does not make progress anymore, e.g. because the convergence thresholds are set tighter than the noise level of the used engine.
Nudged elastic band calculations will stop after the current iteration (i.e. the calculations for all images) is complete.
PES scans will interrupt the currently running geometry optimization and skip the optimization for all further PES points.
PES explorations will terminate after the currently running expedition. No new explorers will be dispatched, but currently active explorers will be allowed to finish.
Note that the Stop keyword in the interactive input file will not interrupt the job in the middle of the numerical calculation of a PES point property, such as a Hessian or stress tensor.
It will also never stop a job that is currently running an engine, and will hence not stop an engine that is calculating these properties analytically.
It is possible to interrupt the numerical calculation of PES point properties using the StopProperties keyword.
We advise users to be careful with this keyword and always combine it with the Stop keyword, as it is generally not possible to skip the evaluation of properties, but continue with a task as the AMS driver level.
(After all, the driver may need the properties that we interrupt.)
echo "Stop" > ams.results/interactive.in
echo "StopProperties" >> ams.results/interactive.in
StopProperties- Type
Bool
- Default value
No
- Description
Makes the AMS driver stop execution during the evaluation of PES point properties. This may for example be used to interrupt the numerical calculation of a Hessian. Note that this just works at the level of the loops used for the **numerical** calculation of the properties, so engines which calculate a property analytically may not be interruptible using this keyword. It is recommended to use this keyword in combination with the generic
Stopkeyword.
As of AMS2021.1 it is not possible to restart the calculation of properties that were interrupted like this. Hence the use of the StopProperties keyword is limited.
Running AMS on compute clusters¶
AMS is parallelized with MPI and can therefore be run in parallel on distributed memory machines, aka compute clusters. See the installation manual for general documentation on how to set up and run all the programs from the Amsterdam Modeling Suite on compute clusters. In this section we give some more advice that is specific to the AMS driver and its engines.
Normally users use the login node to prepare their jobs and input files
somewhere in their home directory, and also want the results of their jobs to
end up there. Quite often, compute clusters are set up such that the user’s home
directory is also mounted on the compute nodes, usually via NFS (Network File
System). Before the introduction of the AMS driver it was not recommended to
cd to the home directory in the submission script and have the compute nodes
execute the job directly there. This was simply due to the fact that a lot of
file I/O was done on temporary files in the present working directory, which in
this case would be on a slow network-mounted file system.
On the other hand, with AMS, switching to the home directory is the preferred way of running on a cluster where the home directory is mounted on the compute nodes. Running in the home directory mounted over NFS does not come with a performance penalty for AMS, but has many advantages. This is because AMS and its engines are already built under the assumption that access to this directory is slow. Basically there are three directories that are used by the AMS driver and its engines:
The starting directory, i.e. the present working directory at the time the AMS driver is started. This folder is generally read-only for AMS, except for creating the results directory there at the beginning of a calculation. Note that all relative paths in the AMS input, e.g. for loading results from previous calculations, are relative to the starting directory. The starting directory is assumed to be on a slow filesystem, but since data is normally only read once from there in the beginning of a calculation, this is in practice not a problem.
The results directory, where the results of a calculation as well as important intermediate steps (e.g. restart files) are collected. It also contains the log file which can be used to monitor a running calculations. The results directory is assumed to be on a slow filesystem, so AMS and its engines will be very careful not to do much disk I/O there. Generally something is only written to the results directory when AMS is sure that it should remain on disk when the calculation finishes. The results directory can also contain some intermediate restart files, so the contents of the result directory should be all that is needed in case the calculation crashes or is killed before it finishes normally.
The scratch directory, the location of which is set with the
$SCM_TMPDIRenvironment variable, see also the installation manual. This directory should be put on a fast disk, e.g. an SSD in the compute node, as it will be used to store temporary results on disk. Users do not really need to care or know about the temporary files in the scratch directory. Normally, any files and directories created in the scratch directory are cleaned up at the end of the calculation. In case of errors, AMS tries to copy anything useful (e.g. the text output of all the different ranks) to the results directory in order to make finding the problem easier. However, for some kinds of crashes (or if theSIGKILLsignal is sent to AMS), the cleanup of the scratch directory might not be performed, in which case users might want to manually check or remove theamstmp_*folders in the scratch directory.
With this setup there is no performance penalty for running directly on a network mounted home directory: Results will just be put there immediately, instead of being copied there at the end of a calculation.
Normally all batch systems provide an environment variable that is set to the
directory from which the job was submitted, which is then where one should
cd in the run script:
#!/bin/sh
if [ -z "$PBS_O_WORKDIR" ]; then
# PBS batch system
cd "$PBS_O_WORKDIR"
elif [ -z "$SLURM_SUBMIT_DIR" ]; then
# Slurm batch system
cd "$SLURM_SUBMIT_DIR"
elif [ -z "..." ]; then
# add other batch systems as necessary ...
cd "..."
fi
export AMS_JOBNAME=myJob
$AMSBIN/ams << EOF
# Normal AMS text input, but with all paths
# relative to where the job was submitted from, e.g.:
LoadSystem previousJob.results/ams.rkf
EOF
With this runscript the AMS driver would make a myJob.results folder in the
directory where the job was submitted from, and there is no need to copy results
around manually in the run script. Furthermore this runscript always produces
exactly the same files in the same locations, no matter if it is run
interactively or submitted to a compute node through the batch system.
Furthermore all paths in the input file can be specified relative to the
location from where the runscript is submitted (normally the folder in which the
runscript is located). This removes the need to copy or specify absolute paths
to previous results, e.g. when restarting calculations. Finally, files useful
for monitoring the running calculation are also conveniently there and not
hidden somewhere on the compute node.
Output¶
AMS produces two ASCII files: standard output and the ams.log file, and produces several binary output data files.
The ams.log file is a very concise summary of the calculation’s progress during the run.
The binary output data files contain job characteristics and computational results produced by AMS and the Engine.
Part of what is written to the binary output files is also written in a human readable form to standard output.
Results directory¶
Note that AMS does not put any of its binary output files and the ams.log file
into the present working directory, as virtually all of the standalone programs
in the suite did. Instead AMS creates a *.results directory, which collects
all result file associated with a job. Here * is replaced by the jobname,
which is set with the AMS_JOBNAME environment variable:
AMS_JOBNAME=methane $AMSBIN/ams << EOF
... see Input example before ...
EOF
This would put all results related to our geometry optimization of methane into
the newly created folder methane.results. (The default name of the results
folder is ams.results if AMS_JOBNAME is not set, see the
environment variables section of this manual for
documentation of all environment variables used by AMS.) In this way users can
easily run multiple jobs in the same directory without danger of clashing output
files, which was a common problem before the introduction of AMS. This new setup
is also more consistent with the graphical user interface, which already
collected all files associated with a specific job into a dedicated results
directory. Note that AMS will by default not overwrite results directories if a
job is rerun or another job is run with the same jobname.
Logfile ams.log¶
Inside of the results directory users will always find the logfile ams.log,
which is written during a running calculation and can be used to monitor its
progress.
The logfile ams.log is generated during the calculation and flushed after (almost) each message that is sent to it by the program.
Consequently, the user can inspect it and see what is going on without being delayed by potentially large system I/O buffers.
Each message contains date and time of the message plus additional info.
Be alert on error messages. Take them seriously: inspect the standard output carefully and try to understand what has gone wrong.
Be also alert to warnings.
They are not necessarily fatal but you should understand what they are about before being satisfied with the results of the calculation.
Do not ignore them just because the program has not aborted: in some cases the program may not be able to determine whether or not you really want to do what appears to be wrong or suspicious.
If you believe that the program displays erratic behavior, then the standard output file may contain more detailed information.
Therefore, in such case save the complete standard output file, together with the logfile ams.log, in case we need these files for further analysis.
Binary output files¶
The results directory contains binary result files in the KF format, which can be opened and inspected with the KFbrowser GUI component. KF stands for Keyed File: KF files are keyword oriented, which makes them easy to process by simple procedures. KF files are Direct Access binary files.
The main
ams.rkfwritten by the AMS driver. It contains high level information about the trajectory that the AMS driver took over the potential energy surface. For a geometry optimization it would for example contains the history of how the systems geometry changed during the optimization as well as the final optimized geometry. For a molecular dynamics simulation it would contain the full trajectory. The format in which this information is written is independent from which engine was used for a calculation.
Note
For a full description of the data on the ams.rkf file, see the KF output files page.
The engine specific main binary output file written by the engine (and partly by the AMS driver). This file is kept for only one special point, e.g. the final geometry in a geometry optimization. The ADF engine writes
adf.rkf(instead ofTAPE21in older versions). The BAND engine writes band.rkf (instead ofRUNKFin older versions). The DFTB engine writesdftb.rkf. If a property, like vibrational modes, is tied to this special point on the potential energy surface, it is stored in this file. Also all engine specific properties are written to the main binary output file, like orbitals in case of a quantum mechanical engine.Table 1 Engine specific main binary output file¶ Engine
main file
ADF
adf.rkf
BAND
band.rkf
DFTB
dftb.rkf
ForceField
forcefield.rkf
MOPAC
mopac.rkf
ReaxFF
reaxff.rkf
External
external.rkf
MLPotential
mlpotential.rkf
ASE
ase.rkf
QuantumEspresso
quantumespresso.rkf
Additionally there might be an engine specific binary output file for every point on the potential energy surface that was visited during the calculation. Like the engine specific main binary output file they contain information tied to a specific point on the potential energy surface. These engine output files all have the extension
.rkf, but their filename is usually somehow descriptive of the point on the PES that they correspond to. Note that one does not always get an engine output file for every PES point that was visited during the calculation. For most applications this would just be too much data.Other engine specific binary (and ASCII) output files written by the engine.
Having multiple different binary output files could be confusing for people that
are used to the single result file that was written by the standalone programs
in ADF<=2017. After all, it brings up the question in which file the desired
property is stored. The general rule is: If the property is tied to a particular
point on the potential energy surface, it is stored in the engine output file
belonging to that particular point.
This includes the Hessian, stress tensor, elastic tensor, normal modes of vibration, phonons,
Raman intensities and other vibrational properties.
If the information depends on the entire trajectory over the PES, it is found in
the main ams.rkf written by the AMS driver.
Standard output¶
The standard ouput file contains in a human readable form part of the job characteristics and computational results produced by AMS and the Engine.
Optimized geometry in xyz format¶
In case of Geometry Optimizations, the optimized geometry is saved as an extended XYZ file in the results directory with the name output.xyz.
Note that the optimized geometry is also stored in the binary file ams.rkf and is printed to the standard output.
AMS environment variables¶
The behavior of AMS related to the output can be modified through a number of environment variables.
AMS_JOBNAMESets the name of a job. This name is used to determine the name of the results folder AMS creates, which is
$AMS_JOBNAME.resultsorams.resultsif this environment variable is not set.
AMS_RESULTSDIRIf this environment variable is set, instead of creating a new results folder, AMS will use the set directory as the results folder. Not that the directory set here will not be created by AMS and therefore has to exist before starting AMS. Note that this environment variable can be used to prevent AMS from creating result folders, by setting
AMS_RESULTSDIR=.. This reproduces the pre-AMS behavior of putting all result files into the directory from which a job is started.
AMS_SWITCH_LOGFILE_AND_STDOUTIf this environment variable is set, AMS will redirect what is normally printed on standard output to a file (
ams.out) in the results directory. Instead the contents of the log file (ams.log) will be printed to standard output while a job is running, allowing users to easily monitor the jobs progress. Note that the log file will still be created normally as if this environment variable was not set. This environment variable is just a convenience feature for users that would always redirect their output into a file and then usetail -fon the log file to monitor the running calculation.
This is an example run-script using the AMS_SWITCH_LOGFILE_AND_STDOUT and AMS_JOBNAME environment variables:
#!/bin/sh
# By setting AMS_SWITCH_LOGFILE_AND_STDOUT, the (more compact)
# logfile will be printed to standard output while the full
# text output of the calculation is redirected to the file
# ams.out in the ams results folder
export AMS_SWITCH_LOGFILE_AND_STDOUT=true
# By default ams creates a folder 'ams.results' and puts the
# results of the calculation there. If we set AMS_JOBNAME, the
# results folder will instead be called $AMS_JOBNAME.results
# (in this case, 'H2_optimization.results')
AMS_JOBNAME=H2_optimization $AMSBIN/ams <<eor
System
Atoms
H 0 0 0
H 0 0 1
End
End
Task GeometryOptimization
Engine DFTB
Model GFN1-xTB
EndEngine
eor
Driver level parallelism¶
See also
See also the GUI tutorial on the parallel scalability of the calculation of elastic tensors.
AMS is a parallel program using MPI for efficient execution on distributed memory machines, aka compute clusters. For most jobs, the AMS driver part of a calculation is computationally not particularly costly and most of the execution time is spent inside of the compute engines. Therefore the main parallelization of AMS is inside of the engines, making sure that a good performance is obtained for tasks such as molecular dynamics or geometry optimizations, which consist of a series of interdependent engine invocations: We need to have completed step \(n\) before we can continue with step \(n+1\).
However, not all workloads are of this sequentially dependent type. Some jobs have a lot of independent work, that can be done in parallel. This kind of trivial parallelizability can be exploited at the AMS driver level: Instead of having all cores collaborate on a single PES point and then doing all needed PES points sequentially, we can just distribute the available PES points over the all the available cores. Normally this leads to a better parallel scaling than the default parallelization inside of the engines: Parallelizing the engines is relatively complicated and often requires a lot of communication between cores. Parallelizing on the driver level on the other hand is very easy, and often the only communication required is at the very end of the calculation, when results are collected.
Note that it is perfectly possible to combine both the in-engine parallelization and the driver level parallelism: At the driver level we could split our e.g. in total 32 cores into 4 groups of 8 cores, and then have each group of 8 use the in-engine parallelization to collaborate on a specific calculation. This is especially useful if the total number of cores is larger than then number of independent calculations we have to do. It might also be that we have a very large number of calculations to do, but not enough memory to let every core work alone on its own calculation, as would be ideal from a parallel scaling point of view.
Because of the two levels of parallelism – both at the driver and the engine level – we call this setup double parallelization.
Starting with the AMS2019.3 release, driver level parallelism is used and configured automatically. That means that the AMS driver will automatically parallelize at the driver level when it is possible and considered advantageous. As such it should normally not be necessary for users to explicitly configure the driver level parallelism.
Driver level parallelism can be used for the calculation of the PES point properties which are derivatives, if these need to be done numerically:
Numerical calculation of forces / nuclear gradients. With a double sided derivative this requires \(6 \times n_\text{atoms}\) independent calculations on geometries with one atom displaced along a cartesian coordinate.
Numerical calculation of the stress tensor for periodic systems. This requires up to 12 calculations for a double sided derivative along the 6 strain directions, but might require less in case some of the strains are symmetry equivalent.
Numerical calculation of the Hessian and normal modes of vibration. This is currently only supported for engines that calculate nuclear gradients analytically and done by numerically differentiating this first (analytic) derivative. As such it requires \(6 \times n_\text{atoms}\) independent calculations on geometries with one atom displaced along a cartesian coordinate.
Numerical calculation of the elastic tensor. This requires 84 independent geometry optimizations on systems with differently strained lattices, with each optimization having a variable number of steps.
Numerical calculation of phonons. This requires at most \(6 \times n_\text{atoms}\) displacements, but might require less in case some of the displacements are symmetry equivalent. Note that the displacements are done in a super cell system, which for many engines will increase the memory requirements, but also improve the in-engine parallel scalability.
The forward and backward displacements along normal modes for the Mode Scanning, Mode Refinement, and Mode Tracking.
There are also tasks using driver level parallelism, e.g. Nudged Elastic Band, for which the calculations of all the images is trivially parallel.
Details of the driver level parallelism, i.e. how much to parallelize at the
driver level, are generally configured for the above mentioned cases on an
individual basis, because one might want a different grouping strategy for each
case. For each case there is a separate Parallel block somewhere in the
input (e.g. ElasticTensor%Parallel for the calculation of the elastic
tensor), which has the following keywords:
Parallel
nGroups integer
nCoresPerGroup integer
nNodesPerGroup integer
End
Note that only one of them should be specified in the input, depending of course on what is the desired strategy for parallelization.
nGroups nSplits all cores evenly into
ngroups. We recommend choosingnsuch that it divides the total number of cores without a remainder.nCoresPerGroup nEach group consists of
ncores. As suchnCoresPerGroup 1results in the maximum possible parallelism at the driver level. We recommend choosingnsuch that it divides the total number of cores without a remainder.nNodesPerGroup nMakes groups from all cores within
nnodes, e.g.nNodesPerGroup 1would make every cluster node into a separate group. Note that this option should only be used on homogeneous compute clusters, where all used nodes have the same number of cores. Otherwise cores from different nodes will be grouped together in very surprising and unintended ways, probably resulting in suboptimal performance.
The optimal grouping strategy and number of groups depends on the total number of cores used in the calculation, the amount of independent tasks to be done in parallel, as well as the parallel scalability of the engine itself. In practice it can be a bit tricky, which is why the grouping strategy is determined automatically since AMS2019.3.
However, sometimes it can be useful to configure the groups manually. Suppose, as an example, that we want to calculate the elastic properties of a bulk material on a 32 core machine. The calculation of the elastic tensor should be done on a relaxed geometry, including relaxed lattice degrees of freedom. We therefore first perform a geometry optimization, before calculating the elastic tensor. In AMS this can easily be done with the following input:
Task GeometryOptimization
GeometryOptimization
OptimizeLattice True
End
Properties
ElasticTensor True
End
But what is the most optimal parallel setup for this calculation? First we recognize that performing a lattice optimization requires the calculation of the stress tensor at every step of the optimization. Assuming that our bulk system does not have any symmetries AMS can exploit, the numerical calculation of the stress tensor (assuming the engine can not calculate it analytically) would require 12 independent strained calculations for every step in the geometry optimization. Once the geometry optimization is converged, we have to perform 84 independent geometry optimizations to determine the elements of the elastic tensor. In summary, the graph of dependencies between all these tasks looks like this:
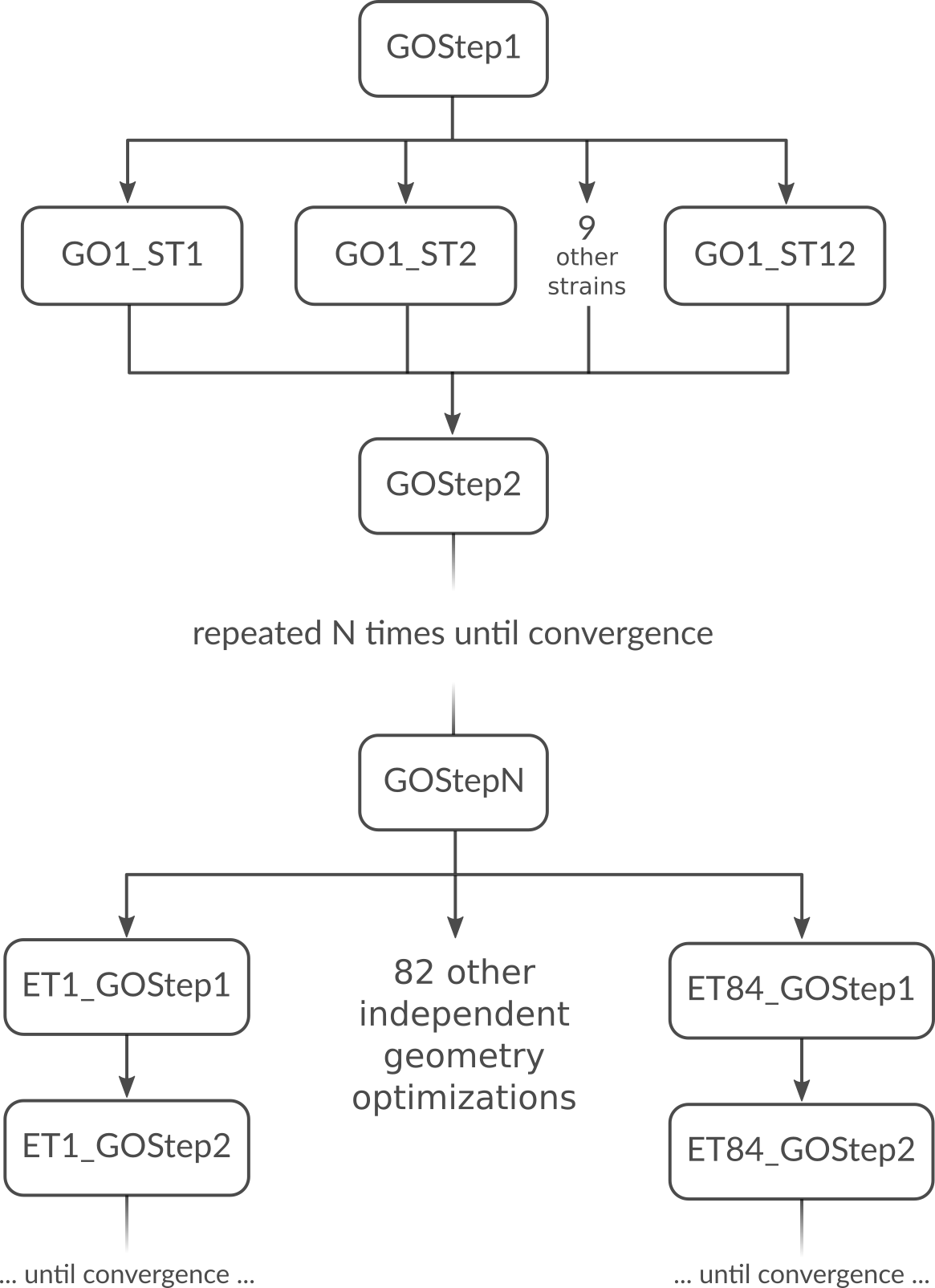
How do we best parallelize this? For the main steps, e.g. GOStep1 there is
no question: We have nothing to do in parallel and all 32 cores work on it
together to finish it as quickly as possible. For the numerical calculation of
the stress tensor we have 12 tasks that can be done in parallel by the 32 cores
in our machine. Now 12 obviously does not divide 32 without a remainder, so
there is no way to split into equally sized groups and do all 12 strains in
parallel. The greatest common divisor of 12 and 32 is 4, so it’s probably best
to split into 4 groups of 8 cores each. This is done with nGroups 4. Each
group would then do 3 of the 12 strained calculations sequentially, using the
in-engine parallelization to speed up the individual calculations. Once the
stress tensor is computed in this way all groups merge and all 32 cores work
together on GOStep2. This splitting and merging now continues until the
geometry optimization is converged. For the elastic tensor we now have 84 tasks
to perform in parallel, where each task is a completely separate geometry
optimization (without optimizing the lattice) of a strained system. 84 tasks is
more than double the number of cores we have. In this case it is probably not
too bad to just run as parallel as possible at the driver level and make 32
“groups” of just one core to throw the 84 tasks at. This is easily done by
setting nCoresPerGroup 1 in the ElasticTensor block. Putting everything
together we should add the following to our input file in order to optimally
utilize our machine for this example calculation:
NumericalDifferentiation
Parallel
nGroups 4
End
End
ElasticTensor
Parallel
nCoresPerGroup 1
End
End
Python interface¶
There is a complete Python interface to AMS, which allows users to set up and run arbitrary AMS jobs, and to conveniently analyze the calculation results directly from Python. In this way AMS jobs can be automatized and complex multi-stage workflows implemented.
The scripting framework is called PLAMS as in “Python Library for Automating Molecular Simulation”, which conveniently can also be read as “Python Layer for AMS”. It is documented in a separate manual:
Pipe interface¶
AMS can interact with other programs using a custom communication protocol. This enables two independent processes to communicate over a pair of data pipes (FIFOs), exchanging data in a highly efficient manner. One of the processes is the “pipe master”, driving the calculation and sending the atoms, coordinates etc. to the other process to perform calculations. The other process is the “pipe worker”, receiving requests from the master, performing the requested calculations and returning the results such as energies and gradients.
For technical details on the AMSPipe protocol see:
AMS as a pipe master¶
The AMS driver can play the role of a pipe master, allowing users to combine the features of the AMS driver with potentials implemented in external programs.
Unlike a traditional external engine, the overhead introduced by the pipe interface is entirely negligible, because the external program is only started once at the beginning of the run and all communication is handled by an efficient binary protocol instead of text files.
This mode is enabled by using Engine Pipe in the input for the master.
Engine Pipe
WorkerCommand /path/to/pipe/worker
EndEngine
WorkerCommand- Type
String
- Description
The command to execute to run the external worker. The command is executed in a subdirectory of the results directory.
All calculations requested by the driver will then be forwarded over the pipe to the worker for processing.
Note
AMS currently must be run in serial (NSCM=1) when serving as a pipe master.
A Python module implementing the worker side of the AMSPipe protocol is available in scm.amspipe.
To facilitate interfacing with various existing computational engines, this module provides the ASEPipeWorker class.
This class can wrap any ASE calculator object and make it serve as a pipe worker.
calculator = ase.calculators.lj.LennardJones()
# calculator.parameters = …
engine = scm.amspipe.ASEPipeWorker(calculator=calculator)
engine.run()
AMS as a pipe worker¶
AMS can also serve as a pipe worker, allowing external drivers to take advantage of its engines.
This mode is enabled by using Task Pipe.
No Geometry, System definition is required on the input because the system will be supplied by the pipe master.
Hint
For most users it will easiest to use this functionality through the new AMSWorker class in the PLAMS library. This class hides all the details of the underlying AMSPipe protocol and provides users an easy way to get very fast access to energies, gradients and other properties from any of the engines in the AMS driver. See the respective page in the PLAMS manual for details.
See also
Additionally AMS can also be driven through the FlexMD library using AMSPipeForceJob:
forcejob = AMSPipeForceJob(mdmol)
forcejob.settings.engine = 'ReaxFF'
forcejob.settings.engineSettings = { 'ForceField': 'Glycine.ff' }