Modeling phosphorescent lifetimes of OLED emitters
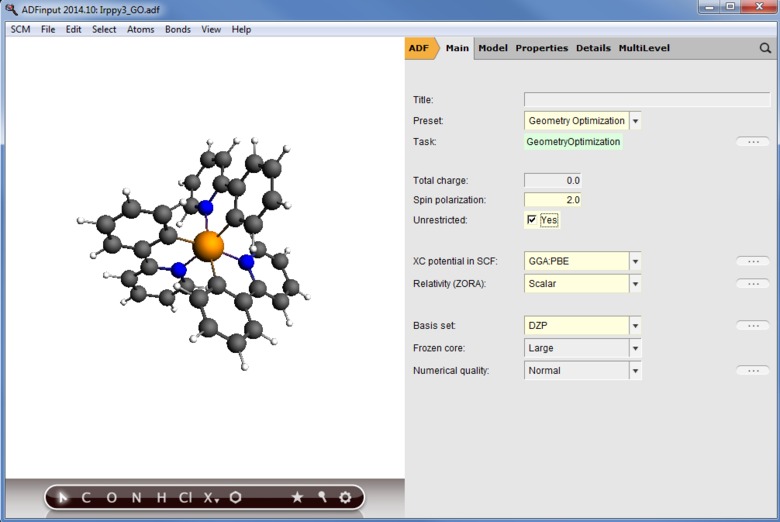
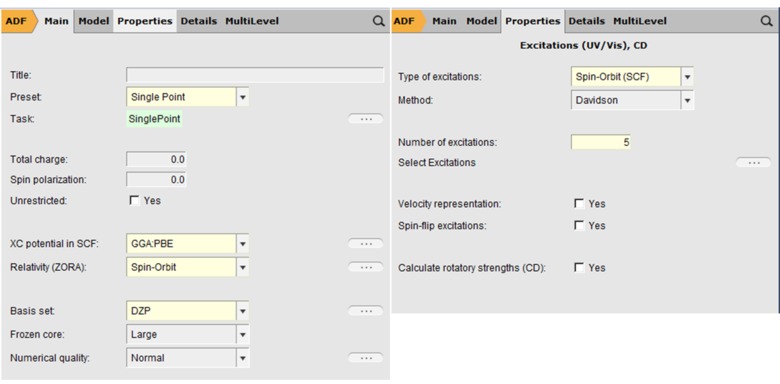
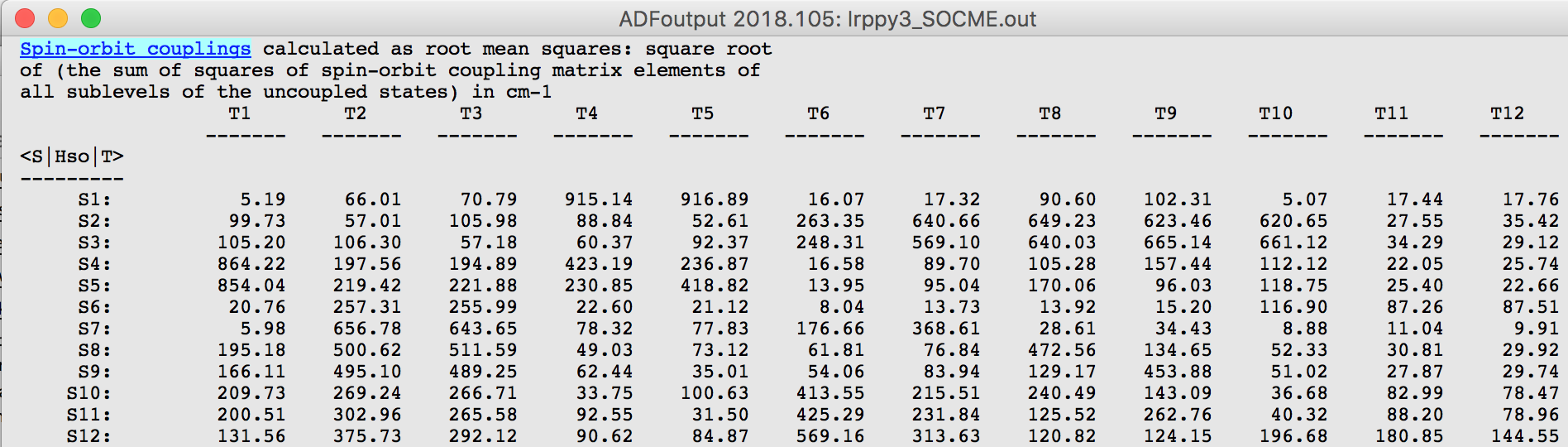
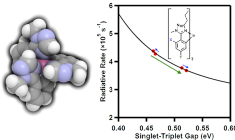
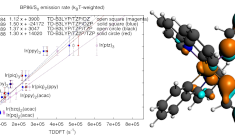
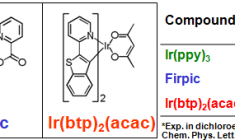
In organic light-emitting diodes (OLEDs), phosphorescent dyes increase the maximum theoretical efficiency from 25% to 100% with respect to fluorescent dyes. To model the spin-forbidden phosphorescence from the triplet state to the singlet ground state, T1 → S0, spin-orbit coupling must be included in TDDFT calculation (SOC-TDDFT). With ADF it is possible to calculate phophorescent lifetimes with SOC-TDDFT, as explained in this guided example for a famous OLED emitter, the 5d transition metal complex Ir(ppy)3.
Example input and output files
While this example is self-contained, it is still helpful to download the sample input and output files.
Essentially the procedure for predicting phosphorescent lifetimes consists of two steps:
- Optimization of the lowest triplet state (T1)
- SOC-TDDFT calculation at the optimized T1 geometry