Stress-strain curve: Fracture point¶
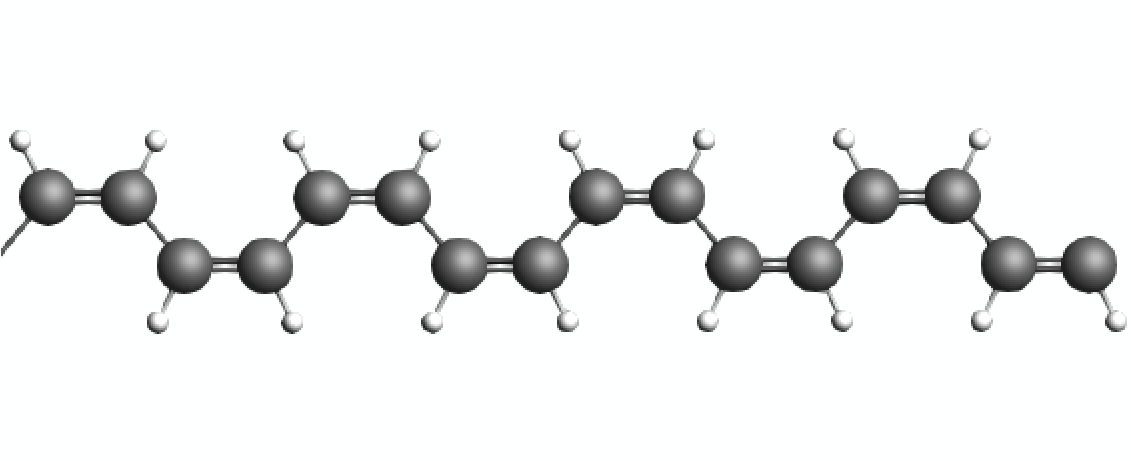
This tutorial demonstrates how to set up a molecular dynamics calculation with an increasingly deformed unit cell in order to study the mechanical properties of a small polymer chain model. During the simulation, the strain on the chain is increased slowly until the initial double bonds of the cis-Polyacetylene are successively converted into their trans configurations. Afterwards, an even larger strain causes the polymer chain to snap which immediately reduces the stress to zero. The stress tensor components computed during the MD simulation are then collected with a small Python script and plotted to demonstrate different changes in the molecular structure of chain.
Note
With AMS2020 and later versions, the deformation of the Polyacetylene chain demonstrated in this tutorial can also be realized using a 1D periodic lattice. To use a 1D periodicity, the deformation of the x-axis needs to be set and the Polyacetylene chain needs to be rotated accordingly.
Step 1: Start the GUI¶
We will set up an MD simulation from the GUI. Alternatively, you can download this PolyStressStrain.run.
 →
→ 
Step 2: Import Structure and Settings¶
We begin by setting the main calculation options for the molecular dynamics simulation.
cis_polyacetylene.xyz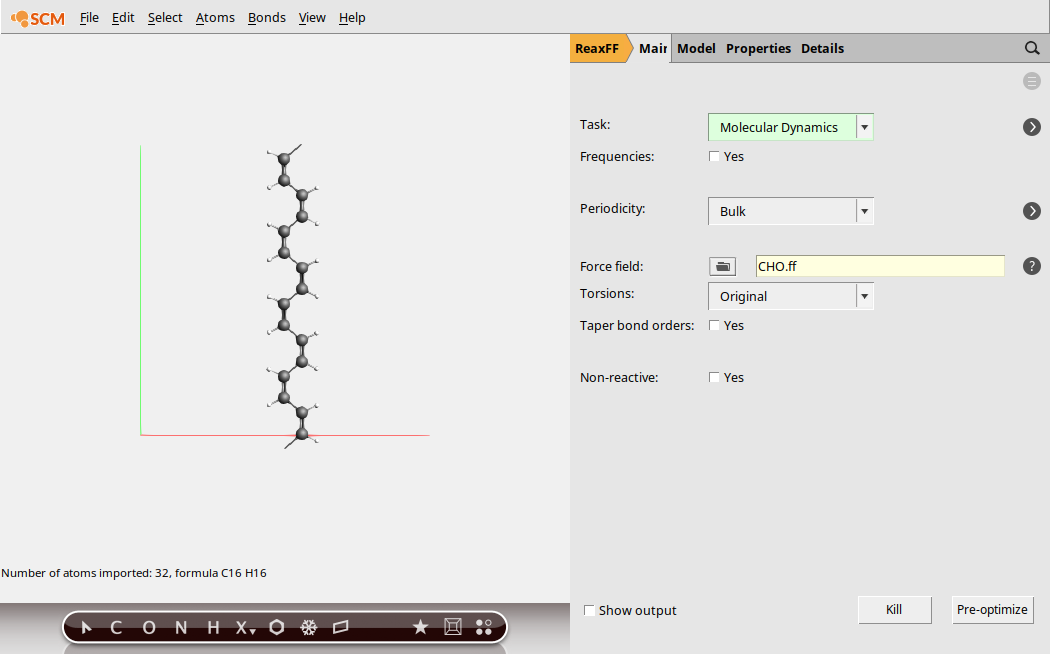
Next, set the options for molecular dynamics:
 next to Molecular Dynamics
next to Molecular Dynamics850000100050000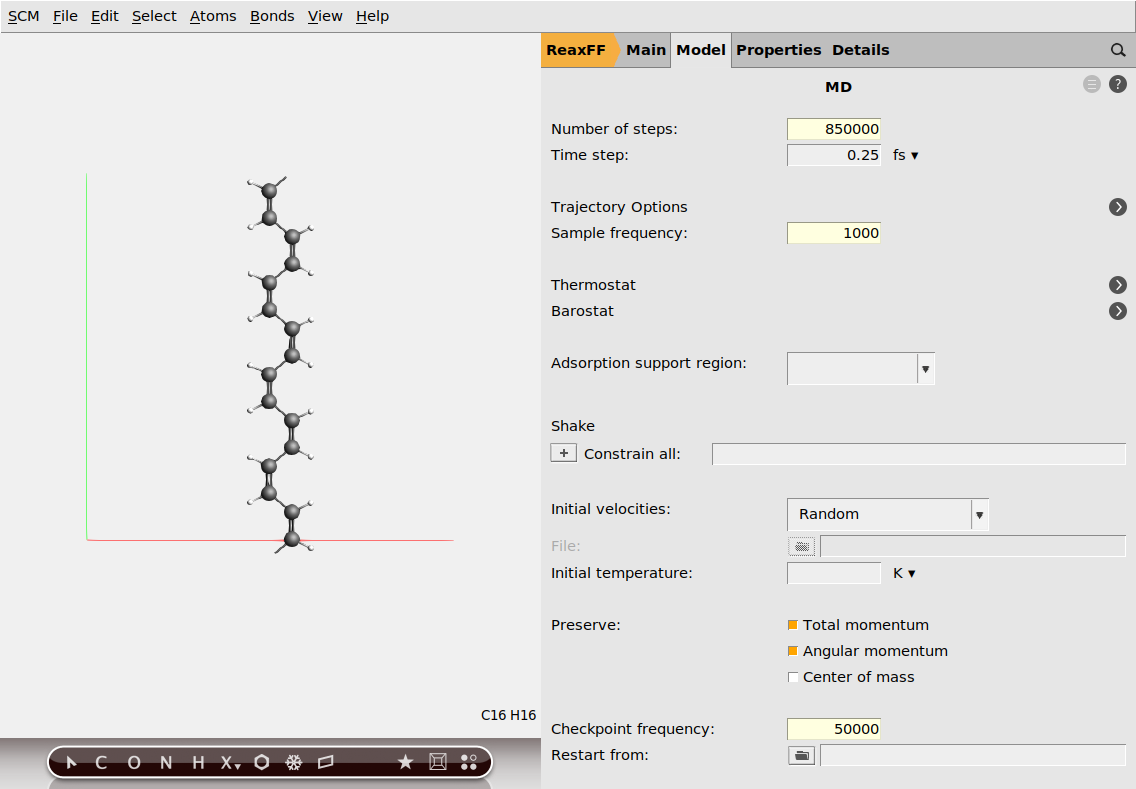
The simulation should run at constant temperature, so we add a thermostat:
 next to Thermostat and add a Thermostat
next to Thermostat and add a Thermostat300.15 K100.0 fs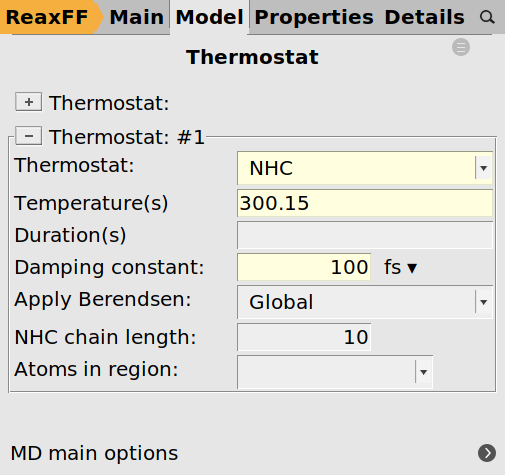
Next, we have to set up the deformation so that the chain is stretched during the simulation.
0.00002 A/fs.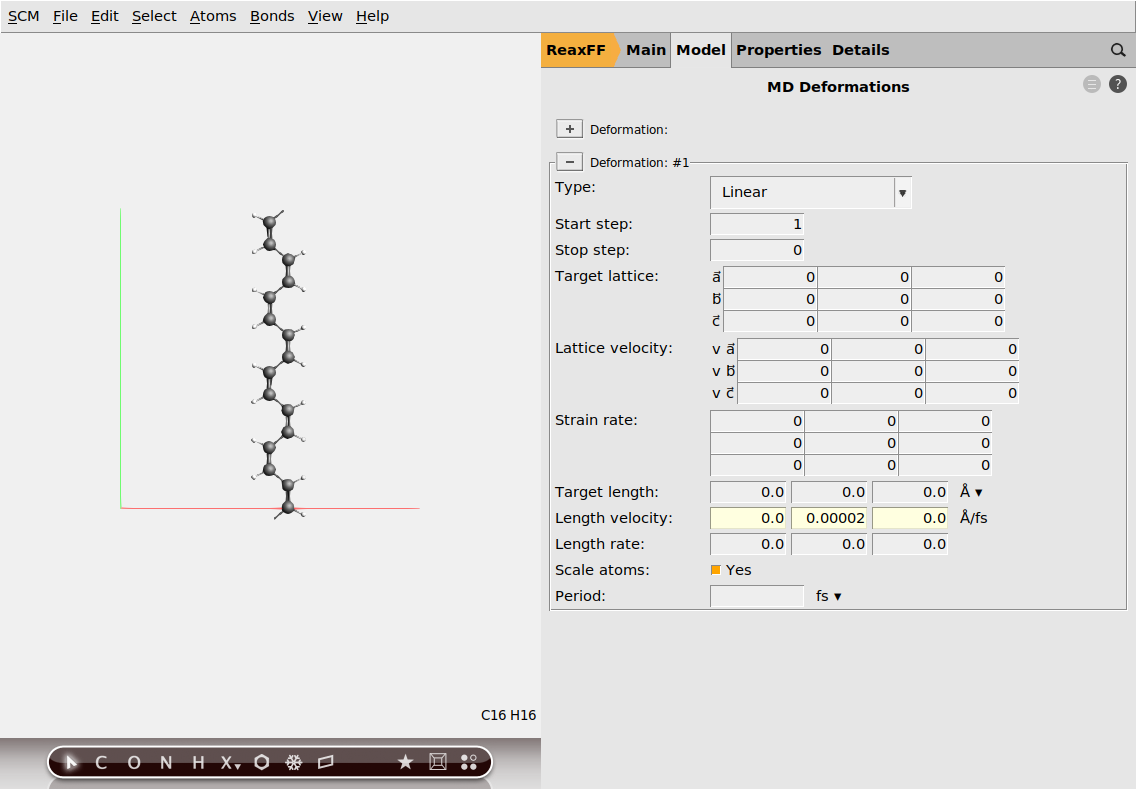
Lastly, we need to calculate the stress tensor

Step 3: Run the Calculation¶
After having set all calculation options we are now ready to start the run
PolyStressStrain
Step 4: Results¶
Once the calculation is finished, we can analyze the results

It is worth noting the distinct segments displayed in the stress/strain plot, as they correspond to various configurations of the Polyacetylene chain. Initially, we started from a cis- configuration. However, during the simulation, as the chain is being pulled, it undergoes a transition whereby some or all of the cis- bonds convert into trans- bonds. Following this transition, the mechanical properties of the chain change, which can be observed through different slopes on the stress/strain graph. Eventually, at a certain strain point, the chain snaps, resulting in an immediate reduction of stress to zero. This occurs as the periodic polymer chain transforms into a molecular entity beyond this critical point.
We can then perform a simple linear regression analysis on this curve:
 button
button
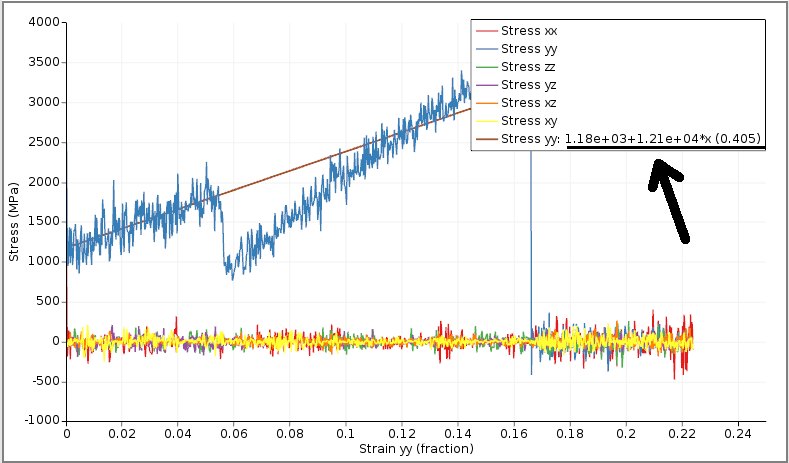
In the legend you can see the regression coefficients for the stress-strain linear fit of the first segment.
Once the calculation has finished, the stress-strain curves can be extracted from the binary results file with the help of a Python script using the PLAMS library.
The script called stress_strain_curve.py can be run from the command line:
$AMSBIN/amspython stress_strain_curve.py PolyStressStrain
Be sure to match the job name correctly.
The stress-strain curve is written to a file called stress-strain-curve.csv:
# strain_x, strain_y, strain_z, stress_xx, stress_yy, stress_zz
0.0000 0.0000 0.0000 -0.000002123540 0.000041449314 -0.000000198040
0.0000 0.0026 0.0000 0.000001083810 0.000039450993 0.000000882455
0.0000 0.0053 0.0000 -0.000006368834 0.000040380759 0.000000145990
0.0000 0.0079 0.0000 0.000000862343 0.000039169395 0.000001048778
0.0000 0.0105 0.0000 0.000000339014 0.000050208909 -0.000000796209
0.0000 0.0132 0.0000 0.000000671946 0.000050569092 0.000001392349
0.0000 0.0158 0.0000 0.000009834386 0.000061383368 0.000003143092
0.0000 0.0184 0.0000 0.000000607648 0.000053138974 0.000005960118
0.0000 0.0211 0.0000 -0.000005062346 0.000046333020 0.000000554734
The resulting stress/strain curve can then be plotted as stress_yy (column 5) against strain_y (column 2) with any plotting software, e.g. matplotlib:

You can download an example script plot_stress.py, which can be run with amspython to generate an image called stress-curve.png.