Thermal conductivity from NEMD

In this tutorial the temperature-dependent thermal conductivity is calculated from a non-equilibrium molecular dynamics (NEMD ) trajectory. The AMS engine used is the UFF force field .

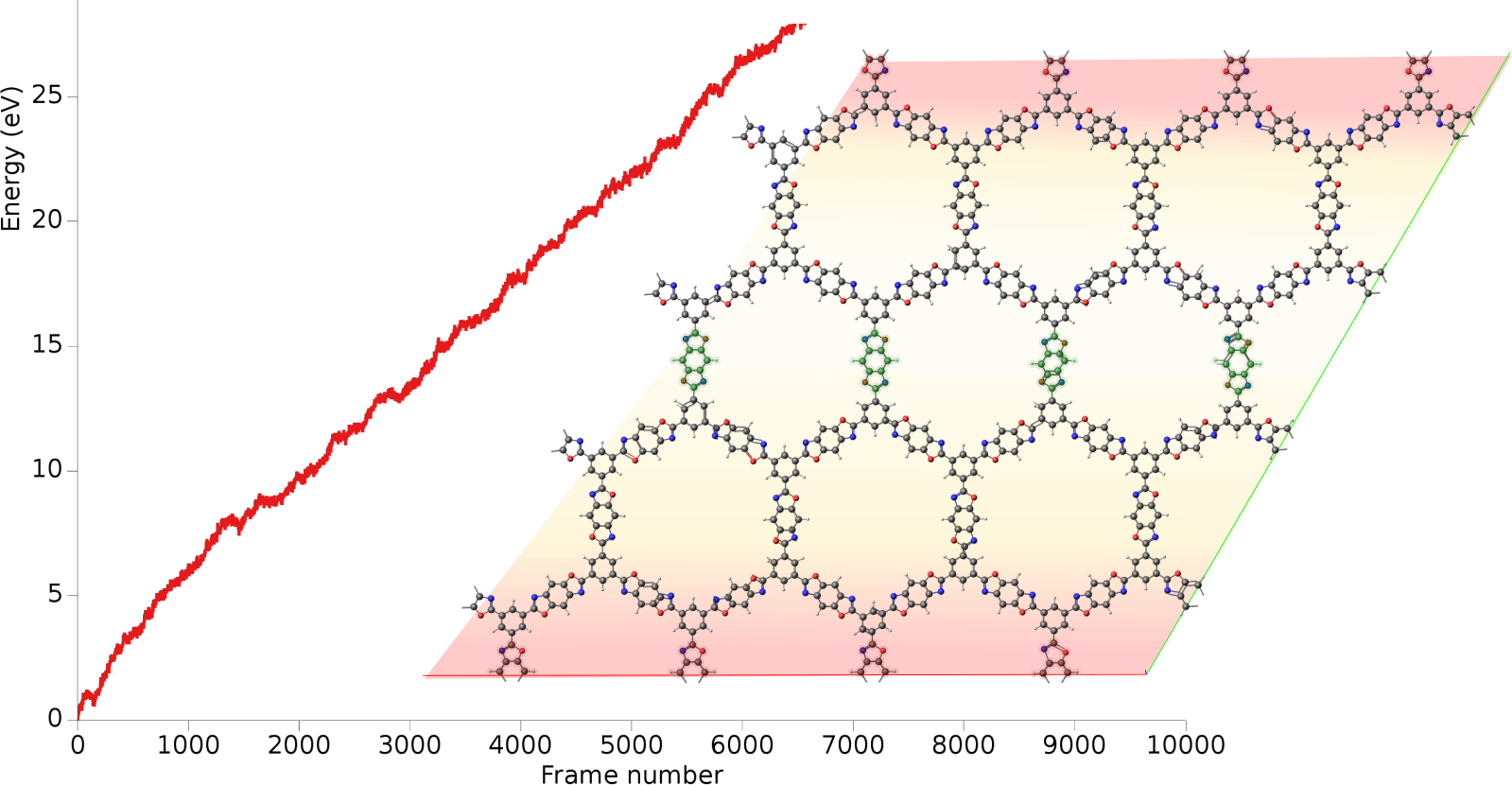
/scm-uploads/doc/Tutorials/_images/T-NEMD-thumbnail.png

A heat flow is realized by running two local thermostats, heat source and heat sink, inside the same molecular structure. The heat source is set to be 10K above the target temperature, while the heat sink is kept 10K below the target temperature. From the energy collected at the heat sink over time and the cross-sectional area, the heat flux and thermal conductivity can be calculated. Both the molecular structure and the workflow were taken from the combined experimental and theoretical study E.M. Moscarello, B.L. Wooten, H. Sajid, L.D. Tichenor, J.P. Heremans, M.A. Addicoat, P.L. McGrier, ACS Appl. Nano Mater. 2022, 5, 10, 13787–13793.

The heat flux Q can be calculated as

\[Q = \frac{dE}{dt}\frac{1}{2S}\]

where S is the cross-sectional area. The heat flux is related to the thermal conductivity via Fourier’s law

\[Q = k\frac{\Delta T}{L}\]

where L is the length of the conduction zone and \(\Delta T = T_{\textrm{source}} - T_{\textrm{sink}}\).

Combining these two equations gives the thermal conductivity k as

\[k = \frac{dE}{dt} \frac{L}{2S\Delta T}\]

Setup

Begin by downloading the input structure BBO_COF1.xyz. The file contains the cartesian coordinates of a benzobisoxazole (BBO)-linked COF for which the thermal conductivity at 80K will be calculated.

Note

The periodic structure has been relaxed with GFN1-xTB (including the lattice), as described in the paper .

1. Download the coordinates BBO_COF1.xyz and import them into AMSinput
2. Change to ForceFieldPanel
3. Choose Task → Molecular Dynamics
/scm-uploads/doc/Tutorials/_images/T-NEMD-1.png

Define a heat source and a heat sink by using regions .

1. Change to the panel Model → Regions
2. Switch on the periodic view, PeriodicViewTool
3. Select the atoms of the source region (hold down SHIFT key for multiple selections)
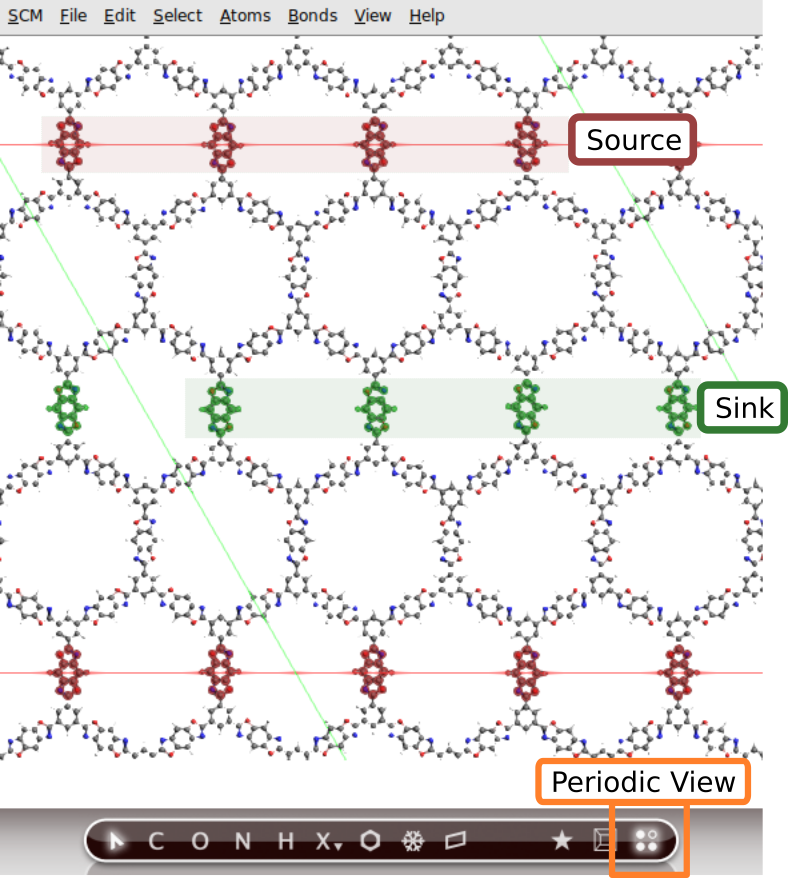
/scm-uploads/doc/Tutorials/_images/T-NEMD-2A.png
4. Click on AddButton to generate a region
5. Enter name | source for the region
6. Repeat steps 3 → 5 with atoms of the sink region
/scm-uploads/doc/Tutorials/_images/T-NEMD-2.png

The source and sink regions can now be connected to two independent thermostats

1. Change to the panel Model → MD… → Thermostat
2. Click on AddButton to generate a thermostat
3. Choose Thermostat → NHC
4. Set Termperature to 90
5. Set Damping constant to 10
6. Choose Atoms in region → source
7. Repeat steps 2 → 6 to generate an NHC thermostat at 70K for Atoms in region → sink
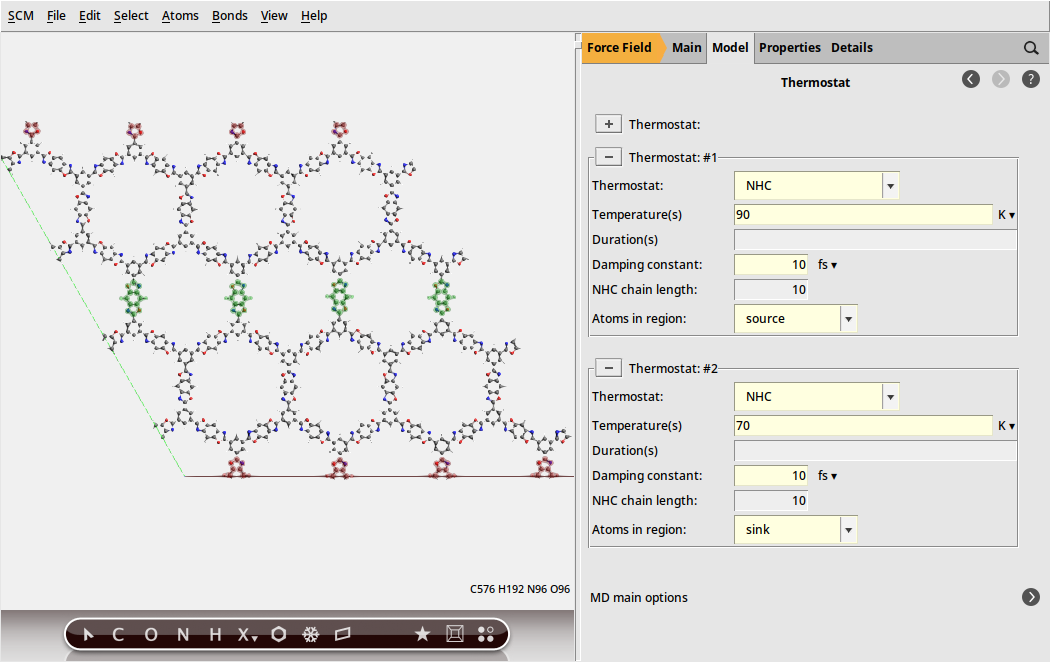
/scm-uploads/doc/Tutorials/_images/T-NEMD-3.png

As the final step, define the settings for the molecular dynamics calculation

1. Change to the panel Model → MD
2. Set Number of steps to 200000
3. Set Time step to 1 fs
4. Set Sample frequency to 1000
5. Set Initial temperature to 80 K
6. Set Checkpoint frequency to 200000. This prevents AMS from writing checkpoint files that needlessly take up disk space.
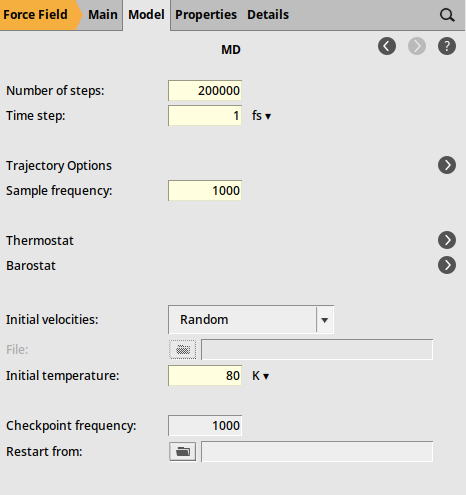
/scm-uploads/doc/Tutorials/_images/nemd_md_settings.png

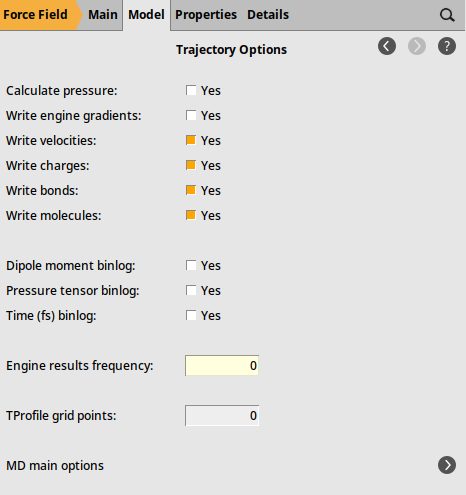
To start the calculation, do

File → Save and File → Run

On a recently modern 12-core desktop computer the calculation will take around 20 minutes.

Results

Once the calculation has finished we can view the results in AMSmovie.

1. From SCMMenu select AMSmovie
2. Make sure that the x-axis on the right hand side shows MD-Time (fs). If it instead shows Frame, toggle Graph → Try to Use Time On X-Axes and restart AMSmovie.

The relevant bits for the NEMD calculation are the energies of the two thermostats as well the time. To visualize these values:

1. Remove the curve of the total energy Graph → Delete Curve
2. Add the energy of the second thermostat MDProperties → NHCTstat2Energy
3. If the Energy is not shown in in eV, double-click on the Energy (eV) y-axis and set the unit to eV.
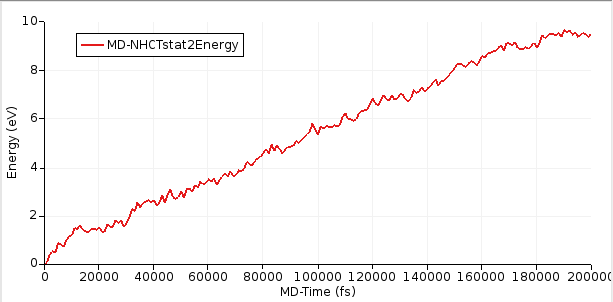
/scm-uploads/doc/Tutorials/_images/nemd_before_linear_fit.png

After the simulation has equilibrated, this curve should increase linearly with time. In this tutorial, we ran a relatively short simulation of 200 ps but ideally it would be run for much longer.

Starting with AMS2023, the slope of the curve can easily be calculated inside AMSmovie.

1. Graph → Analysis
2. Switch to the Linear Regression panel
3. Click the AddButton next to Name
4. In the Start field, enter 100000
5. Click OK
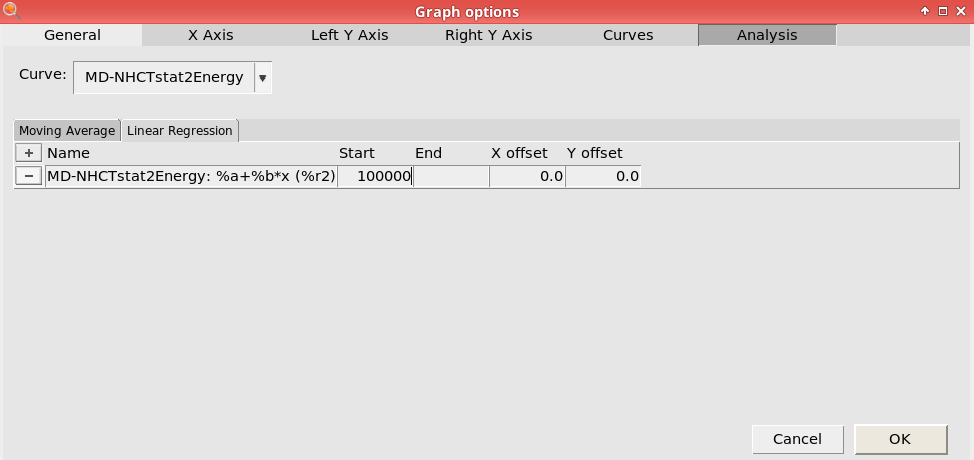
/scm-uploads/doc/Tutorials/_images/nemd_graph_options.png

This will perform linear fit starting from 100,000 fs. Here, we consider the first 100,000 fs to be part of the equilibration period.

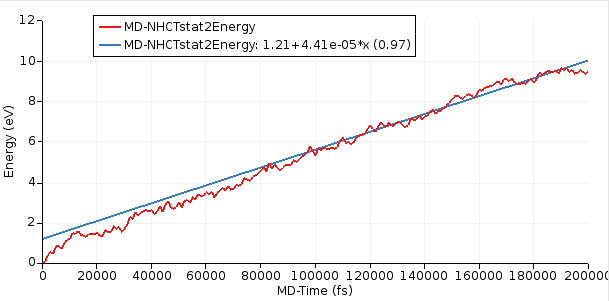
/scm-uploads/doc/Tutorials/_images/nemd_after_linear_fit.png

From the above figure, you see that the slope = dE/dt = 4.41 × 10⁻⁵ eV/fs = 7.07 × 10⁻⁹ J/s.

S is the cross-sectional area, i.e. the area from which heat enters the system, that can be calculated from the lattice vectors a and c of the system:

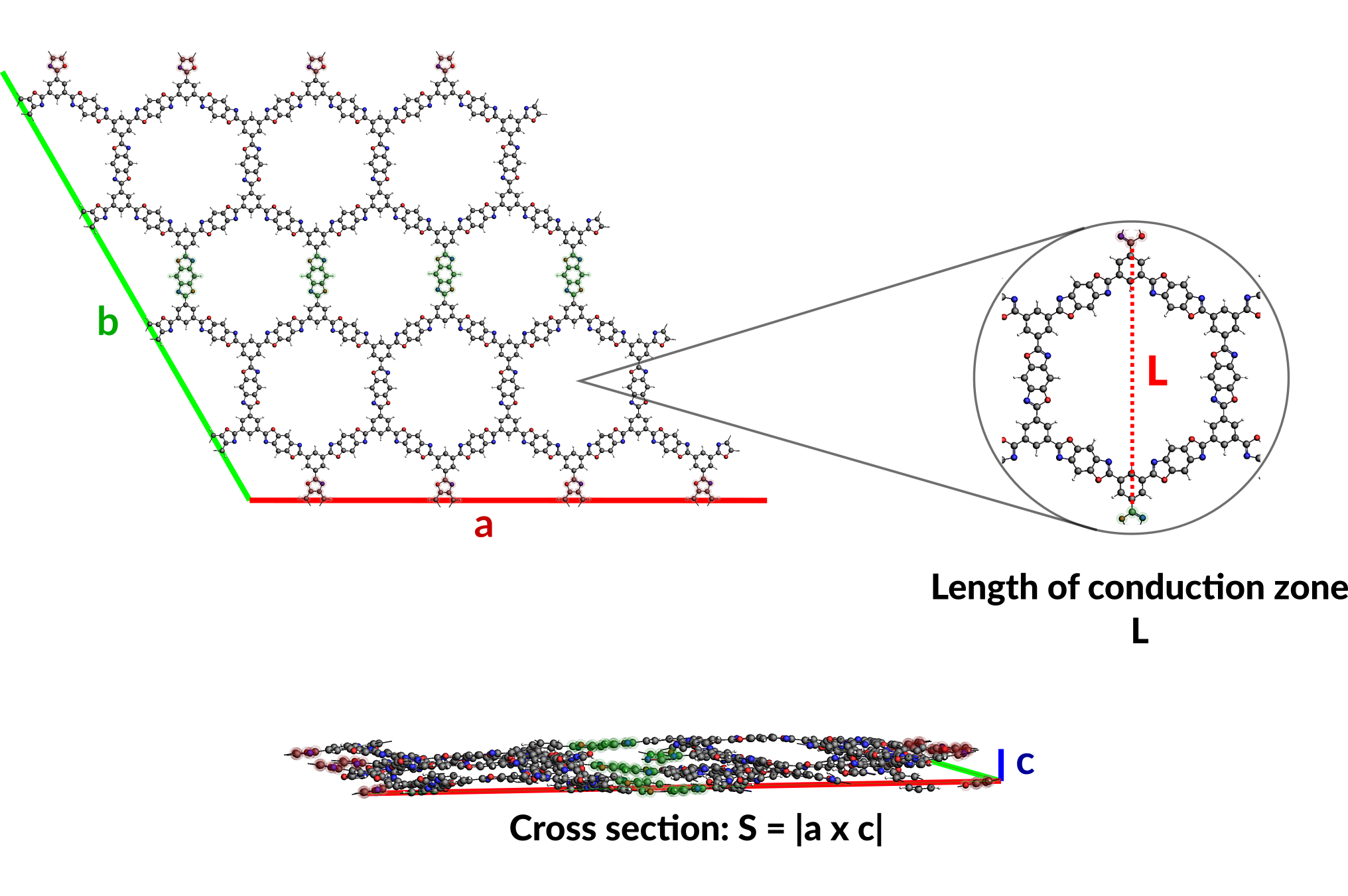
/scm-uploads/doc/Tutorials/_images/definitions.png
1. In the AMSinput window, switch to the Model → Lattice panel
2. Read off the area S = 281.97 Ų.
3. The conduction length L is half the y-component of the b lattice vector: L = 72.305 /2 = 36.15 Å.
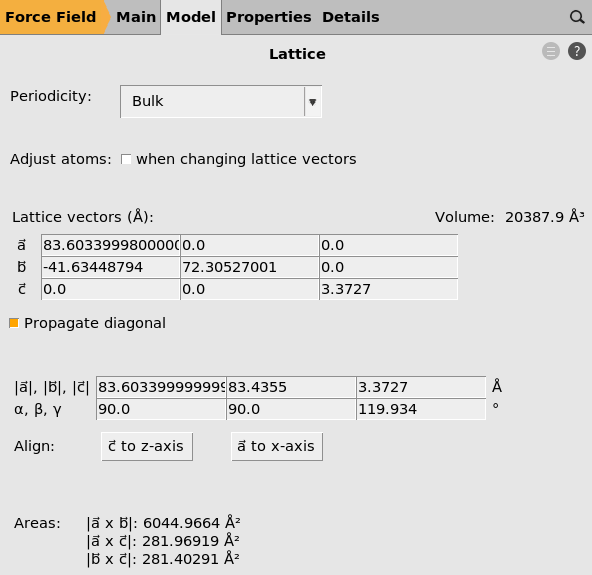
/scm-uploads/doc/Tutorials/_images/nemd_lattice.png

Recall the thermal conductivity k:

\[k = \frac{dE}{dt} \frac{L}{2S\Delta T}\]

The factor 2 stems from the periodic boundary conditions because the heat can flow in two directions.

Inserting the above numbers (with ΔT = 90 - 70 = 20 K) yields k = 0.23 W m⁻¹ K⁻¹ (experimental value: 0.195 W m⁻¹ K⁻¹)

Note

Due to the non-deterministic nature of the MD thermostats and the fitting procedure, the result of this tutorial can vary slightly. Still, the thermal conductivity should be reasonably close to the experimental value.

Easier calculation with Python

You can also use for example the below Python script to automate the procedure of performing the linear fit and the unit conversions:

#!/usr/bin/env amspython
from scm.plams import *
import numpy as np


def main():
    # Unit conversion factors
    eV_to_J = Units.convert(1.0, "eV", "J")
    fs_to_s = Units.convert(1.0, "fs", "s")
    ang_to_m = Units.convert(1.0, "angstrom", "m")

    # length L and cross-sectional area S
    L = 36.15 * ang_to_m  # m
    S = 281.9 * ang_to_m**2  # m^2

    # manually calculated slope and delta_T
    dEdt = 4.41e-5 * eV_to_J / fs_to_s  # J s^-1 = W
    delta_T = 20  # K

    # automatically calculated slope
    # job = AMSJob.load_external("jobname.results")
    # dEdt = get_slope(job, min_time_fs=100000)
    # delta_T = get_delta_T(job)

    # calculate thermal conductivity k
    k = (dEdt * L) / (2 * S * delta_T)

    print(f"Thermal conductivity: {k:.3f} W m^-1 K^-1")


def get_slope(job, min_time_fs=0):
    """
    Calculates the (absolute value of the) slope of NHCTstat2Energy.

    Discards the first min_time_fs from the trajectory.

    Returns: float. The slope in W ( = J/s)
    """
    from scipy.stats import linregress

    time = job.results.get_history_property("Time", history_section="MDHistory")
    time = np.array(time)  # time in fs

    nhctstatenergy = job.results.get_history_property("NHCTstat2Energy", history_section="MDHistory")
    nhctstatenergy = np.array(nhctstatenergy)  # energy in hartree

    ind = time >= min_time_fs
    time = time[ind]
    nhctstatenergy = nhctstatenergy[ind]

    result = linregress(time, nhctstatenergy)

    # take absolute value, convert to watt (J/s)
    slope = np.abs(result.slope) * Units.convert(1.0, "hartree", "J") / Units.convert(1.0, "fs", "s")

    return slope


def get_delta_T(job):
    """
    Assume there are two Thermostats and take the difference of their temperatures

    Returns: float. The difference in temperature in Kelvin
    """
    t = job.settings.input.ams.MolecularDynamics.Thermostat
    assert isinstance(t, list) and len(t) == 2, f"get_delta_T can only be called if there are exactly two thermostats"

    delta_T = abs(float(t[0].Temperature) - float(t[1].Temperature))
    return delta_T


if __name__ == "__main__":
    main()