Viscosity: Green-Kubo relation

This tutorial will show how to calculate the viscosity of liquid benzene using the Green-Kubo relation:

\[\eta = \frac{V}{k_{\rm{B}}T} \int_0^\infty <P_{\alpha\beta}(0)P_{\alpha\beta}(t)> \rm{d} t\]

where \(\eta\) is the viscosity, \(V\) is the cell volume, \(k_{\rm{B}}\) is the Boltzmann constant, \(T\) is the temperature, \(P_{\alpha\beta}\) is an off-diagonal component of the pressure tensor, and \(t\) is time. The function \(<P_{\alpha\beta}(0)P_{\alpha\beta}(t)>\) is an autocorrelation function with the average taken over all time origins and off-diagonal components (αβ is yz, xz, or xy).

The pressure tensor equals the stress tensor plus a kinetic contribution. This tutorial was also featured in our video tip of the week series

Step 1: Create a box of benzene

Create a box of 40 benzene molecules with density ρ = 0.875 g cm-3 (experimental room-temperature density of benzene) using the Builder in AMSinput.

Start AMSinput
Switch to the ForceField panel: ADFPanel → ForceFieldPanel
Edit → Builder
Set Density to 0.875 g cm-3
Tick Use number of molecules
In SMILES or file, enter the SMILES for benzene: c1ccccc1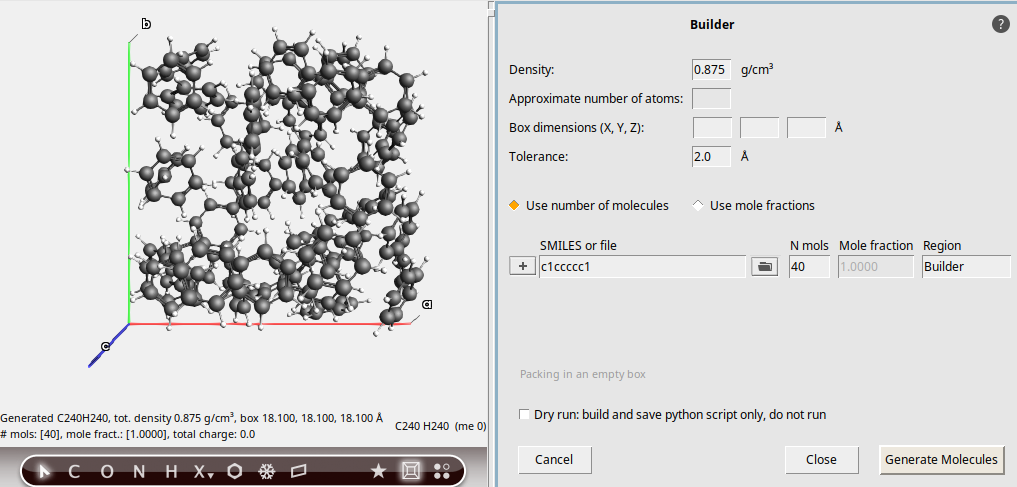
Set N mols to 40
Click the Generate Molecules button
Click the Close button at the bottom of the Builder window
/scm-uploads/doc/Tutorials/_images/builder1.png

The molecules are generated at random positions and orientations. Before calculating the viscosity with a production simulation, it is very important to equilibrate the positions with an equilibration simulation.

Step 2: Set up the equilibration simulation

The next step is to set up the details of the simulation.

Set Periodicity → Bulk
Set Type → GAFF
Check the Automatic atom typing checkbox
Set Task → Molecular Dynamics
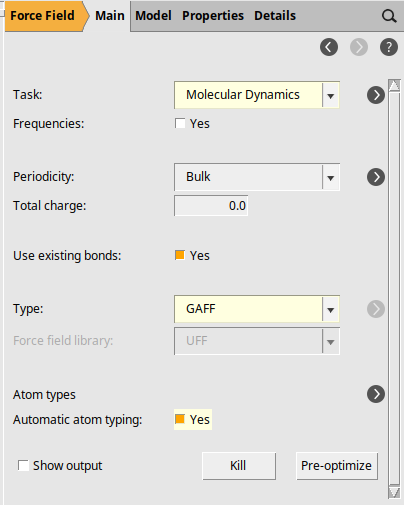
/scm-uploads/doc/Tutorials/_images/settings1.png
Model → MD or MoreBtn next to Task: Molecular Dynamics
Number of steps: 10000
Time step: 1 fs
Initial temperature: 298 K
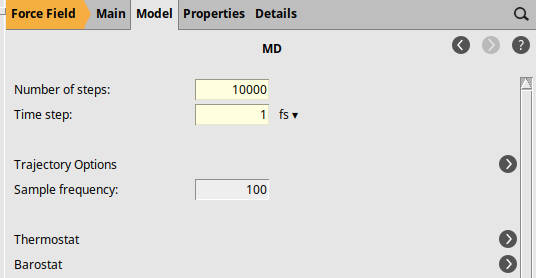
/scm-uploads/doc/Tutorials/_images/viscosity_mdpanel.png
Click on MoreBtn next to Thermostat
Click on the AddButton to add a thermostat
Thermostat: Berendsen
Temperature(s): 298
Damping constant: 100 fs
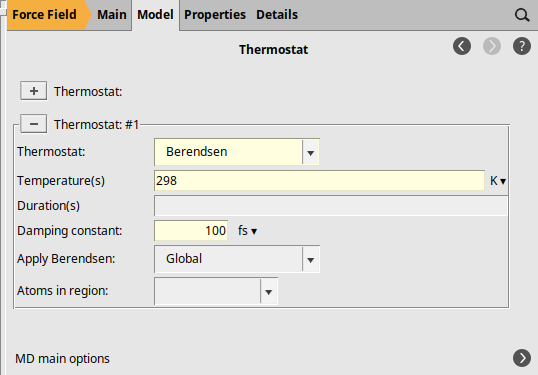
/scm-uploads/doc/Tutorials/_images/viscosity_thermostat.png

Now we will run your set-up:

Use the File → Run command
When asked to save your input, save it with the name Benzene

Keep the AMSinput window open while the simulation runs. It should finish in a few minutes.

When the simulation has finished, a dialog pops up
Select Use MD velocities from results for AMS MD restart
Choose Yes, new job
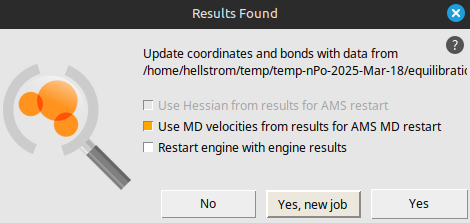
/scm-uploads/doc/Tutorials/_images/use_md_velocities.png

Step 3: Set up the production simulation

For the production simulation, we make the following changes compared to equilibration:

  • Increase number of MD steps

  • Change thermostat from Berendsen to NHC

  • Calculate and store the pressure tensor at every timestep (BinLog). This will be used to calculate the viscosity.

Note: The viscosity of benzene is quite low, so we can run a rather short MD simulation. Usually you would use a smaller time step than 1 fs.

Model → MD
Set Number of steps to 400000
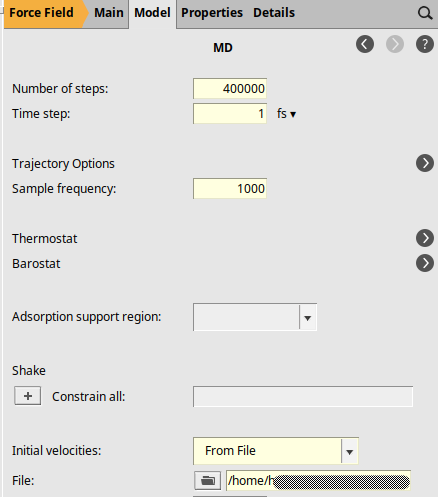
/scm-uploads/doc/Tutorials/_images/prod_main_md.png
Click the MoreBtn next to Trajectory Options
Check Calculate pressure
Uncheck Write velocities
Uncheck Write charges
Uncheck Write bonds
Uncheck Write molecules
Check Pressure tensor binlog
Check Time (fs) binlog
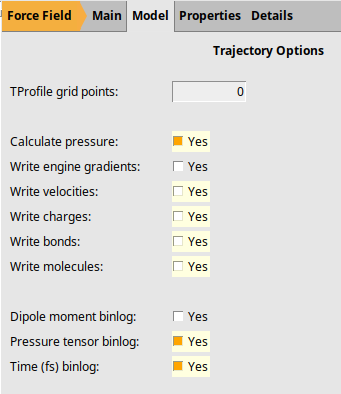
/scm-uploads/doc/Tutorials/_images/viscosity_trajectory_options.png
Use the File → Run command
When asked to save your input, save it with the name Benzene_production

Important

Double-check that the pressure is calculated. At the start of the simulation, open the logfile (SCM → Logfile), and make sure that numerical values (and not “n/a”) is printed for the pressure. If there is no pressure, then stop the simulation and double-check that you followed all instructions.

Note

Running this calculation may take up to 2 hours.

Step 4: Analyze the simulation results

Wait until the production calculation has finished, and then open it in AMSmovie.

Select the production job in AMSjobs and start AMSmovie: SCM → Movie
Press the Play button (the triangle pointing right at the left bottom of the AMSmovie window)
MD Properties → Autocorrelation function
Property → Viscosity From Bin Log
Press the button Generate ACF
/scm-uploads/doc/Tutorials/_images/ACFsettings.png

This brings up several graphs in AMSmovie. The bottom graph contains the viscosity as a function of upper integrand limit:

\[y(t) = \frac{V}{k_{\rm{B}}T} \int_0^{t}<P_{\alpha\beta}(0)P_{\alpha\beta}(\tau)> d\tau\]
Select the top graph with the energy curves and press Backspace. Answer Yes to delete the graph.
Select the next graph with the autocorrelation function and press Backspace. Answer Yes to delete the graph.
Select the next graph with the Fourier transform and press Backspace. Answer Yes to delete the graph.

Now only the curve with the viscosity vs. time remains:

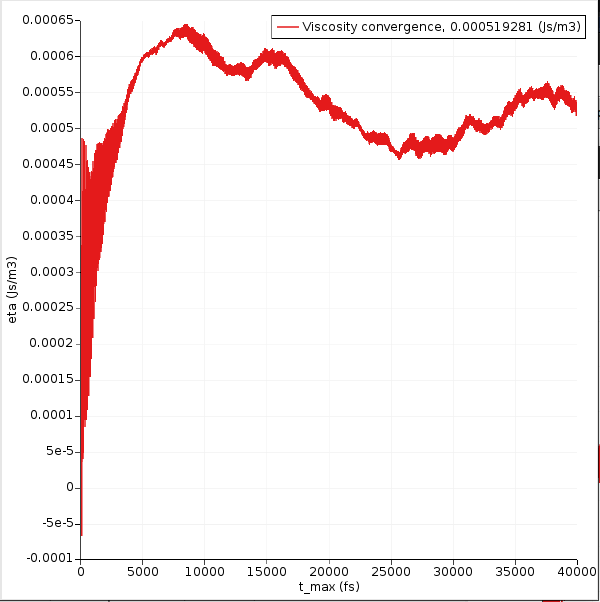
/scm-uploads/doc/Tutorials/_images/viscosity_curve_40000.png

In the ideal case this graph will converge to a constant value as t → \(\infty\). This usually requires very long simulations. Your graph may look different.

Important

Even if it looks like the curve converges, the calculated viscosity may still change if you increase the simulation length.

Longer simulations are always better.

In this case, the integral seems to converge to a value of about 0.0006 J s / m 3, or 0.6 mPa s. The value that is printed in the legend is the final value, but because of noise it may be different from the average value in the “flat” region. Typically, if the curve starts to decrease in value, it is a sign of noise and not of signal.

The experimental room-temperature viscosity of benzene is about 0.5 mPa s.

See the Python script section for how to extract the value of the viscosity with Python code. This is useful if the viscosity plot does not fully converge.

Important considerations

  • The simulation needs to be well equilibrated

  • The viscosity is often sensitive to the supercell size. Use a larger supercell with more benzene molecules for a better value.

  • The integral must converge in the long time-limit. You may want to increase the simulation time.

  • The biggest contribution to the integral comes at short correlation times. It is therefore necessary set the PressureTensor BinLog option, so that the pressure tensor is stored at every time step.

  • In general, make sure to equilibrate the density of the liquid first using an NPT simulation, before running an NVT simulation as above. (the above example used the experimental density, but that may not be suitable for the used force field)

  • Better and more reliable viscosity values can most likely be obtained using the APPLE&P or GFNFF force fields.

Python script

Check out the PLAMS example for calculating the viscosity with Green Kubo.