Diffusion coefficient

In this tutorial we will compute the diffusion coefficients of Lithium ions in a Li_0.4S cathode by means of molecular dynamics simulations with the ReaxFF engine.

The systems and workflows presented here are originally described in the publication ReaxFF molecular dynamics simulations on lithiated sulfur cathode materials Phys. Chem. Chem. Phys. 17, 3383-3393 (2015).

The tutorial consists of the following steps:

• Importing a CIF file

• Manipulating the structure (e.g. inserting particles) and equilibrating the system

• Creating an amorphous structure by simulated annealing

• Calculating diffusion coefficients from MD trajectories

If you wish, you can download the already-relaxed amorphous Li_0.4S structure Li04S_amorphous.xyz and jump directly to the diffusion coefficient calculation

See also

Importing the Sulfur(α) crystal structure

1. Open a new AMSinput window

2. Switch to ReaxFF: →

To speed up the calculations, we will use a smaller system than the one described in the publication. The crystal structure can be directly imported from a CIF file:

1. Download the CIF file by clicking here

2. In AMSinput: File → Import Coordinates

3. Select the CIF file you just downloaded using the file dialog window

Generating the Li_0.4S system

We first need an xyz file of a single Lithium atom:

1. Open a new AMSinput: SCM → New Input

2. Draw a single Li atom

3. File → Export coordinates → .xyz and give it the name “Li.xyz”

4. Close the AMSinput window without saving

We use the builder functionality of AMSinput to randomly insert 51 Li-atoms into our Sulfur system.

See also

A better way of building the Li_0.4S system is to use Gran Canonical Monte Carlo (GCMC). See also the Voltage profile from Grand-Canonical Monte Carlo tutorial.

1. Click on Edit → Builder

2. Next to “Fill box with”, set the number to 51

3. Click on the folder and select the “Li.xyz” you just made

4. Set Distance to 1.0 Å

5. Click on Generate Molecules

6. Click on Close

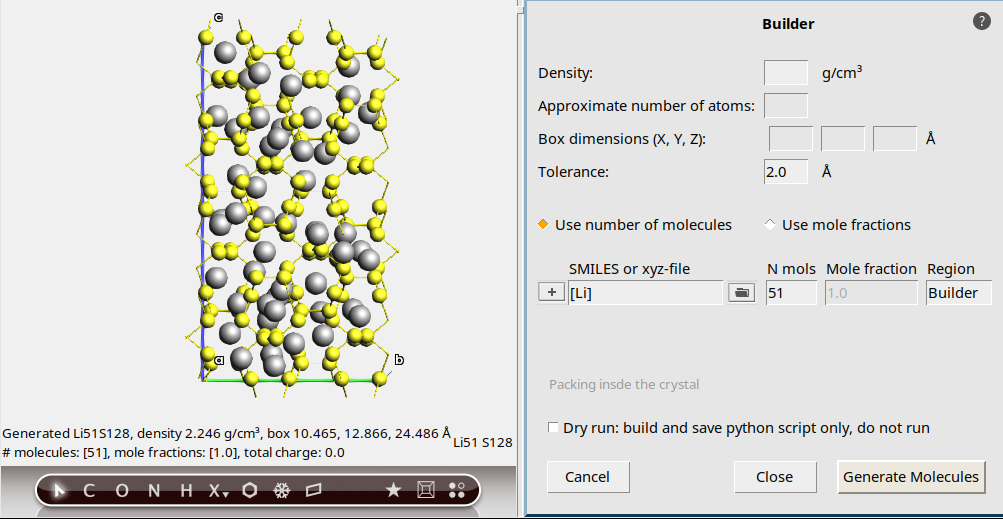
We now need to relax the geometry by running a geometry optimization including lattice relaxation:

1. In the main panel, select Task → Geometry Optimization

2. Click on the folder next to Force Field and select LiS.ff

3. Details → Geometry Optimization

4. Tick the Optimize lattice checkbox

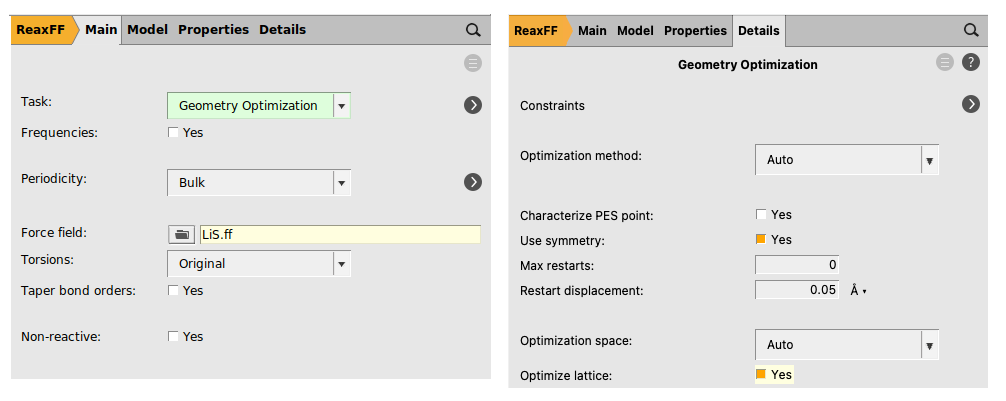
We are now ready to run the Li_0.4S relaxation calculation:

1. File → Save As… and give it an appropriate name (e.g. “LiS_optimization”)

2. File → Run

3. Click yes when asked if the structure in AMSinput should be updated

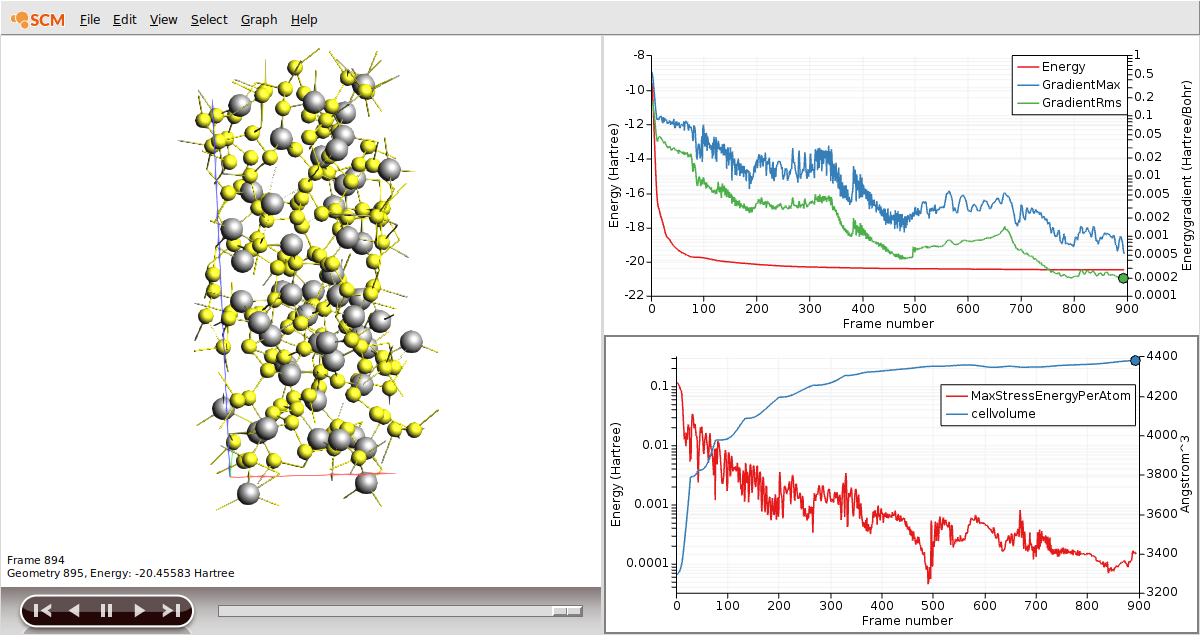
The volume of the unit cell should have increased significantly during the optimization (from about 3300 ų to about 4400 ų):

1. Open AMSmovie by clicking on SCM → Movie

2. In AMSmovie, click on Graph → Cell volume

3. Click on play to see the movie of the geometry optimization

Creating the amorphous systems by simulated annealing

Amorphous systems can be created with a Molecular Dynamics simulation by slowly heating up the system followed by a rapid cool-down.

As in the publication, we will anneal up to 1600 K followed by a rapid cool-down to room temperature. In order to speed up the calculation, only 30000 steps are calculated here.

1. In the main panel, select Task → Molecular Dynamics

2. Click on next to Task: Molecular Dynamics to go to the MD details

3. Set the number of steps to 30000

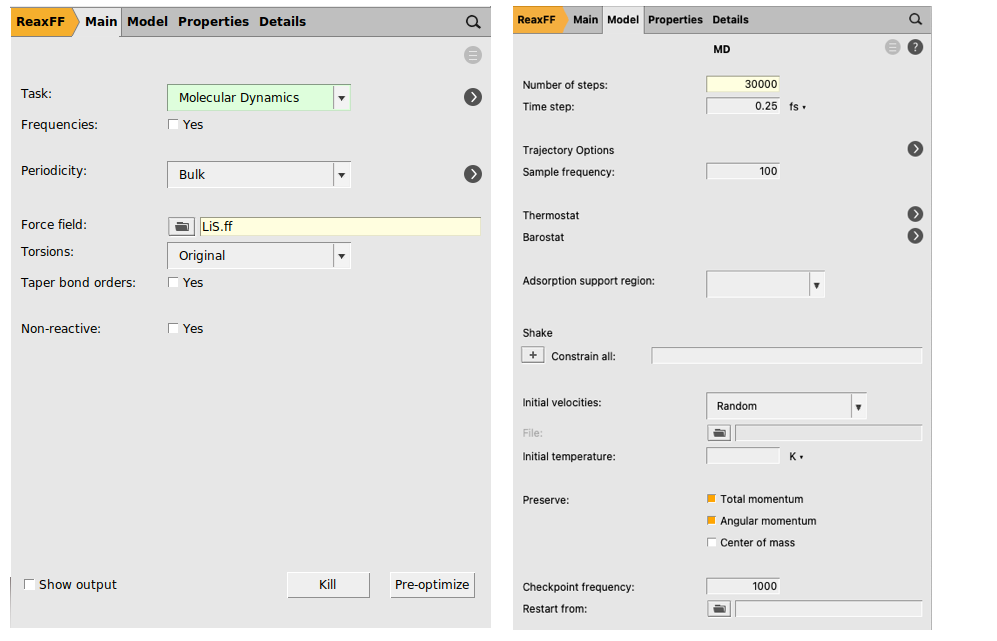
We will now set up the following temperature profile:

1. From start until step 5000: T = 300 K (constant)

2. From step 5000 to step 25000: heating up from 300 K to 1600 K

3. From step 25000 to step 30000: cooling down from 1600 K to 300 K

For more details on temperatures and pressure regimes, see the AMS manual on MD.

1. Click on next to Thermostat to go to the thermostat details

2. Click on to add a new thermostat

3. Select Thermostat → Berendsen

4. In Temperature(s), set the values 300 300 1600 300

5. In Duration(s), set the values 5000 20000 5000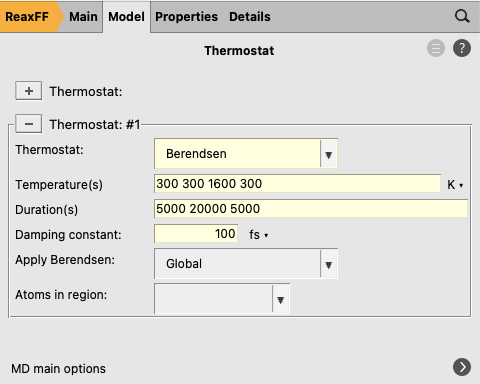

6. Set the damping constant to 100 fs

We are now ready to run the Li_0.4S simulated annealing calculation:

1. File → Save As… and give it an appropriate name (e.g. “LiS_simulated_annealing”)

2. File → Run

3. Click yes when asked if the structure in AMSinput should be updated

In AMSmovie you can follow the progress of the MD simulation, and you’ll be able to see the three temperature regimes:

1. Open AMSmovie by clicking on SCM → Movie

2. In AMSmovie, click on MD Properties → Temperature

3. Click on play to see the movie of the MD simulation

We now need to relax the geometry of our new amorphous system by running a geometry optimization including lattice relaxation (as we did before):

1. In the main panel, select Task → Geometry Optimization

2. Details → Geometry Optimization

3. Tick the Optimize lattice checkbox

4. File → Save As… and give it an appropriate name (e.g. “LiS_amorphous_optimization”)

5. Run the calculation

6. Click yes when asked if the structure in AMSinput should be updated

Calculating the diffusion coefficients

We are now ready to run the final MD simulation to compute the Lithium diffusion coefficient D at T=1600 K.

You can calculate the diffusion coefficient in two different ways:

• Through the slope of the mean squared displacement (MSD, recommended):

\[MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle\]

\[D = \textrm{slope(MSD)}/6\]

• Through the integration of the velocity autocorrelation function (VACF, this requires setting sampling frequency to a small number):

\[D = \frac{1}{3} \int_{t=0}^{t=t_{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t\]

Important

Because of finite-size effects, the diffusion coefficient depends on the size of the supercell (unless the supercell is very large). Typically, you would perform simulations for progressively larger supercells and extrapolate the calculated diffusion coefficients to the “infinite supercell” limit.

Set up and run the production simulation

We will use a minimal proof-of-principle setup of 10000 equilibration steps followed by only 100000 production steps:

1. In the main panel, select Task → Molecular Dynamics

2. Click on next to Task: Molecular Dynamics to go to the MD details

3. Set the number of steps to 110000

4. Set the Sample frequency to 5 (this writes both the atomic positions and velocities to disk every 5 steps)

5. Click on next to Thermostat to go to the thermostat details

6. Set the Type to Berendsen

6. Set the Temperature to 1600 K

7. Clear the Duration field

8. Set the damping constant to 100 fs

Tip

If you use the MSD to calculate the diffusion coefficient, you can set Sample frequency to a higher number (giving a smaller trajectory file).

Note

The time between two steps on the trajectory file will be sample_frequency * time_step = 5 * 0.25 fs = 1.25 fs.

We are now ready to run the calculation:

1. File → Save As… and give it an appropriate name (e.g. “LiS_MD_1600K”)

2. File → Run

3. You can follow the progress of the calculation in AMSMovie and AMStail (SCM → Logfile)

Diffusion coefficient through MSD (recommended)

After the calculation has finished, open it in AMSmovie:

1. In AMSMovie select MD Properties → MSD

2. In Steps set 2000 - 22001

3. Set Atoms to Li

4. Set Max MSD Frame to 5000 (corresponding 5000*1.25 fs = 6250 fs).

5. Click on Generate MSD

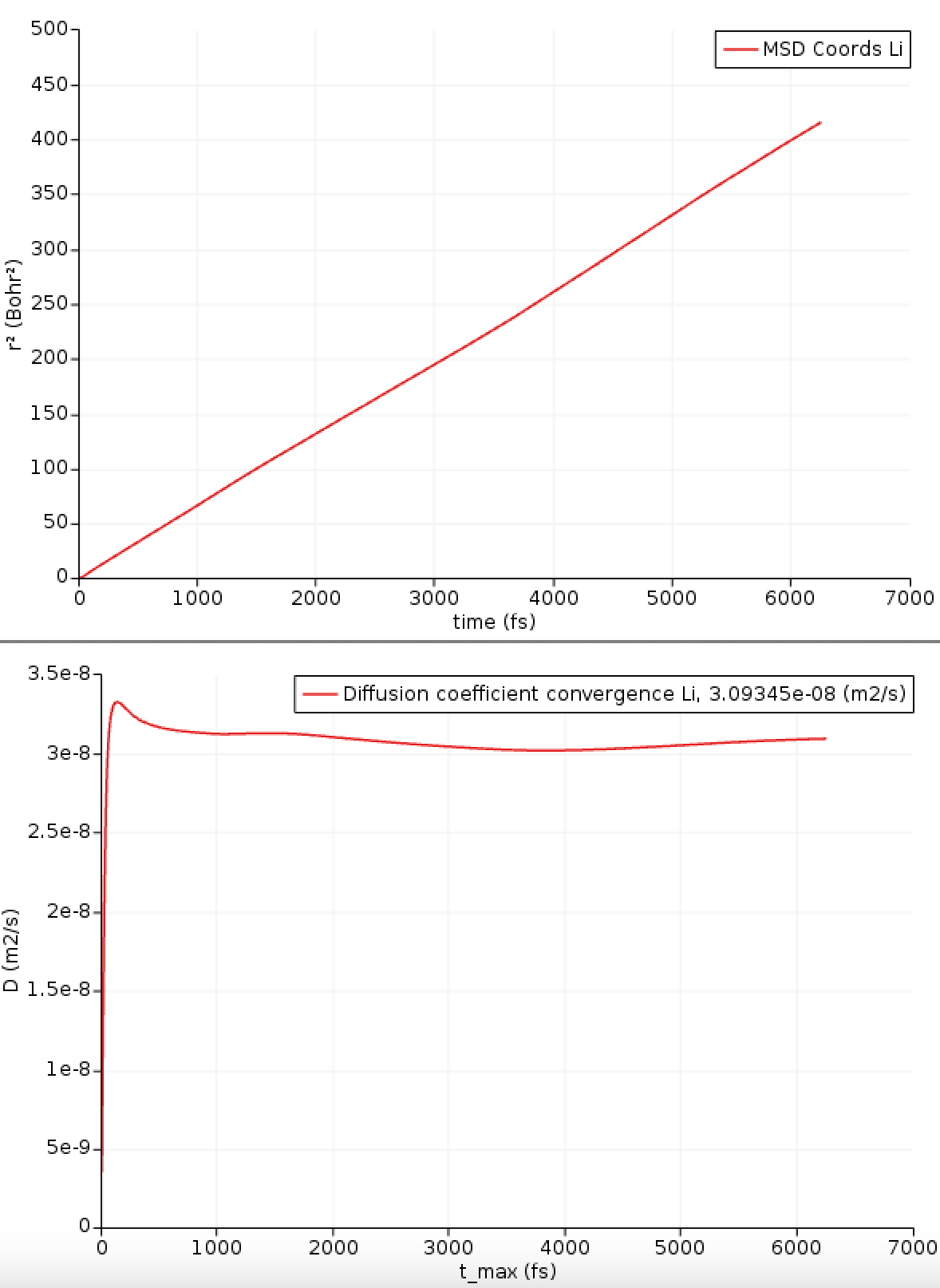
Your results may look a bit different because of the short MD simulation and random initial velocities.

The MSD is the straight line in the above figure. If the MSD line is not straight, it means that you need to run a longer simulation to gather more statistics. It is calculated for times up to 6250 fs (controlled by the Max MSD Step option in the MSD window).

The other curve in the above figure shows the slope of the MSD divided by 6, calculated by performing a linear fit on the MSD from the “Start Time Slope” (that can be set in the MSD window) to each point on the MSD. The curve thus corresponds to the diffusion coefficient D. It should ideally be perfectly horizontal.

Here, the curve seems to converge to a value around 3.09 × 10⁻⁸ m² s⁻¹.

Thus, D = 3.09 × 10⁻⁸ m² s⁻¹.

Diffusion coefficient through VACF

After the calculation is finished, we can obtain the Li diffusion coefficient by computing the velocity autocorrelation function for the Li atoms:

1. In AMSMovie select MD Properties → Autocorrelation function

2. In Steps set 2000 - 22001

3. Select Property → Diffusion Coefficient (D)

3. Set Atoms to Li

4. Set Max ACF Step to 5000 (corresponding 5000*1.25 fs = 6250 fs).

6. Click on Generate ACF

This plots

• the velocity autocorrelation function,

• the Fourier transform of the velocity autocorrelation function (power spectrum),

• the integral of the velocity autocorrelation function divided by 3 (diffusion coefficient)

In this case, only the bottom plot is of interest to us. It should ideally become perfectly horizontal (converge) for large enough times.

Here, the value of the diffusion coefficient D = 3.02 × 10⁻⁸ m² s⁻¹ is approximately equal to the value obtained through the use of MSD analysis.

Extrapolate to lower temperatures

Calculating the diffusion coefficient at 300K would require a very long trajectory. However, it is possible to provide an upper bound to the Li diffusion by means of extrapolation from elevated temperatures using the Arrhenius equation:

\[D(T) = D_0 \exp{(-E_a / k_{B}T)}\]

\[\ln{D(T)} = \ln{D_0} - \frac{E_a}{k_{B}}\cdot\frac{1}{T}\]

where \(D_0\) is the pre-exponential factor, \(E_a\) is the activation energy, \(k_B\) is the Boltzmann constant, and \(T\) is the temperature. The activation energy and pre-exponential factors can then be obtained from an Arrhenius plot of \(\ln{(D(T))}\) against \(1/T\). In order to extrapolate the diffusion coefficients for Li_0.4S we calculate trajectories for at least four different temperatures (600 K, 800 K, 1200 K, 1600 K) for each system. One can then extrapolate the diffusion coefficient to lower temperature.

For an example on how to do this with a Python script, see Molecular Dynamics with Python.