Analysis of the VCD spectrum of Oxirane with VCDtools¶
Step 1. Start ADFinput¶
For this tutorial we again prefer to work in the Tutorial directory:
- Start ADFjobsClick on the Tutorial folder iconNext start ADFinput using the SCM menuSelect the SCM → New Input command
Step 2: Create your oxirane molecule¶
These are the coordinates of the oxirane molecule:
C -1.44589917 -0.26968372 -0.00000000
C 0.02774960 -0.35459913 -0.00000000
O -0.64012001 0.88449058 -0.00000000
H -1.94641916 -0.41741698 0.97962259
H -1.94641916 -0.41741698 -0.97962259
H 0.50817848 -0.55867470 -0.97957478
H 0.50817848 -0.55867469 0.97957478
Copy-paste these into ADFinput:
- Select the coordinates on this page (in your browser)Paste them in ADFinput
Now you should have the oxirane molecule.

To ensure chirality two hydrogen atoms should be changed to deuterium atoms:
- Select two hydrogen atoms diagonally across from each other (holding shift)Select the Atoms → Details (Color, Radius, Mass) command
The input area changes to display the atom details menu.
- Set the masses of both selected Hydrogens to 2 by entering the number after the “M:”

- Pre-optimize
Step 3: Optimize the geometry¶
The next step is to optimize the geometry using ADF:
- Click on the ‘Main’ tab in the input field.Select the Geometry Optimization taskSelect ‘GGA:BP86’ as XC functionalSelect ‘none’ for frozen core
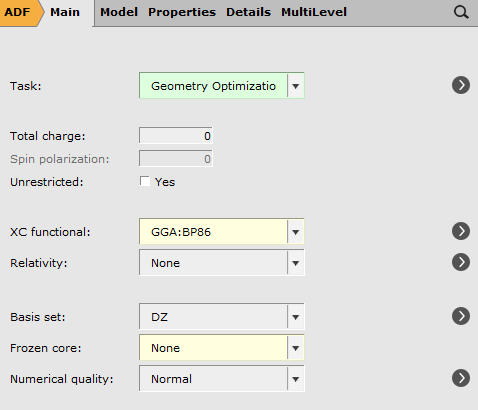
Now run ADF:
- Select the File → Run commandClick ‘Yes’ in the pop-up to save the current inputIn the file select box, choose a name for your file (“Oxirane”) and click ‘Save’
Now ADF will start automatically, and you can follow the calculation using the logfile that is automatically shown.
- Wait until the optimization is ready (should take about one minute)Click ‘Yes’ when asked if you want to update the coordinates
Step 4: Calculate the VCD intensities¶
The next step is to calculate the VCD spectrum with ADF:
- Select the Frequencies taskUse the panel bar Properties → VCD to go to the VCD panelClick the box ‘Calculate VCD intensities:’

Leave the rest of the settings identical to the geometry optimization run the calculation.
- Select the File → Run commandClick ‘Yes’ in the pop-up to save the current inputClick ‘Yes’ (this will replace your geometry optimization job)
Wait until the optimization is ready (should take about two minutes)
Step 5: Analyze the VCD Spectra¶
Next start analyzing the VCD spectrum with ADFspectra. To open the spectra:
- SCM → Spectra
Basically, two types of analysis methods are offered by the analysis program VCDtools. First, it can visualize the properties relevant for the VCD intensity, i.e., the Electric and Magnetic Dipole Transition Moments (EDTM and MDTM) and the normal mode motion. Second, a ‘General Coupled Oscillator’ (GCO) analysis can be performed.
Normal modes can be selected either by clicking in the spectrum or by clicking in the ‘Vibrations Window’. After a normal mode is selected the vibration will be shown in the molecule and some details will be given in the right side of the ‘Vibrations Window’.
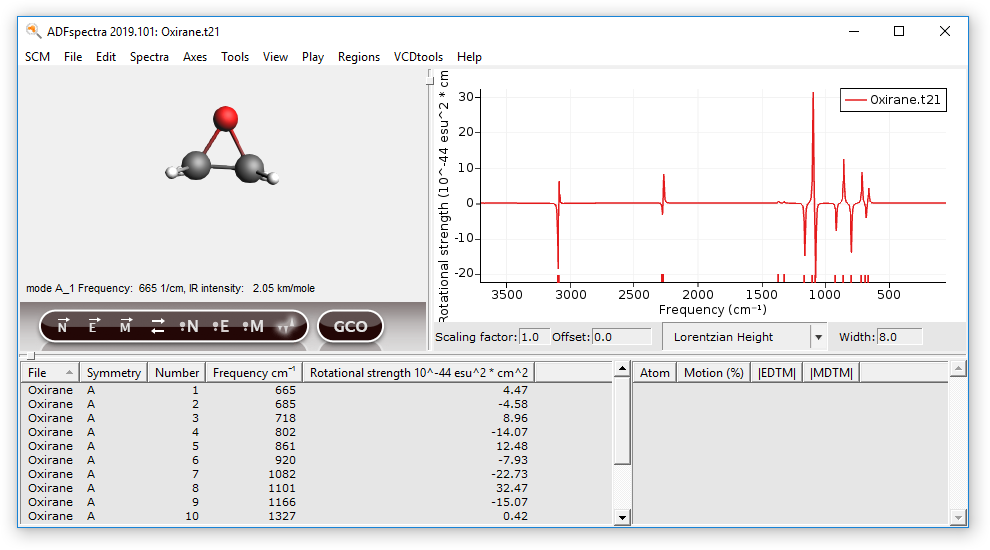
- Select normal mode 15, a large negative peak at 3100 wavenumbersIn the ‘Vibration Window’’ click the header EDTM to sort the atoms accordingly.Click on the row with the highest electric dipole transition moment.
Now one of the hydrogens should be selected. In general, atoms with a high contribution to the EDTM are important for the VCD intensity. To show this a GCO analysis will be performed in the following.
- Select the VCDtools → Default Visualization for GCO Analysis

The atom sizes are now scaled by their EDTM and the nuclear displacement vectors are shown as arrows. To scale the size of these arrows, use the “up” and “down” keys. Using these visualization settings, we immediately see that two of the C-H groups are important for the VCD signal in this normal mode. You can change which vectors are visualized, the phase of these vectors and the scaling of the atoms by clicking the buttons under need the molecule. The buttons that are active will have a glow effect.
The next step in a GCO analysis is to select VCD active fragments:
- Select one of the important C-H groups by pressing the ‘shift button’ while clicking on the atoms.Select the Regions → Set Selection As → New Region commandSelect the other important C-H groupSelect the Regions → Set Selection As → New Region command again

The two important regions will be highlighted by transparent red and green spheres. Additional tools for setting up the regions can be found under the “Regions” menu.
- Select the Regions → Save Regions commandEnter a Name (for example ‘NM15’)Press the ‘Return’ -key or press save
The current regions will have been saved in the ‘.results’ folder in the file ‘Regions.txt’ and can be loaded by the command: Regions → Load Regions → ‘Name’.
To determine whether the coupling between two important C-H groups is important to the rotational strength it can be decomposed using the GCO formalism.
- Click the GCO analysis button with the text ‘GCO’
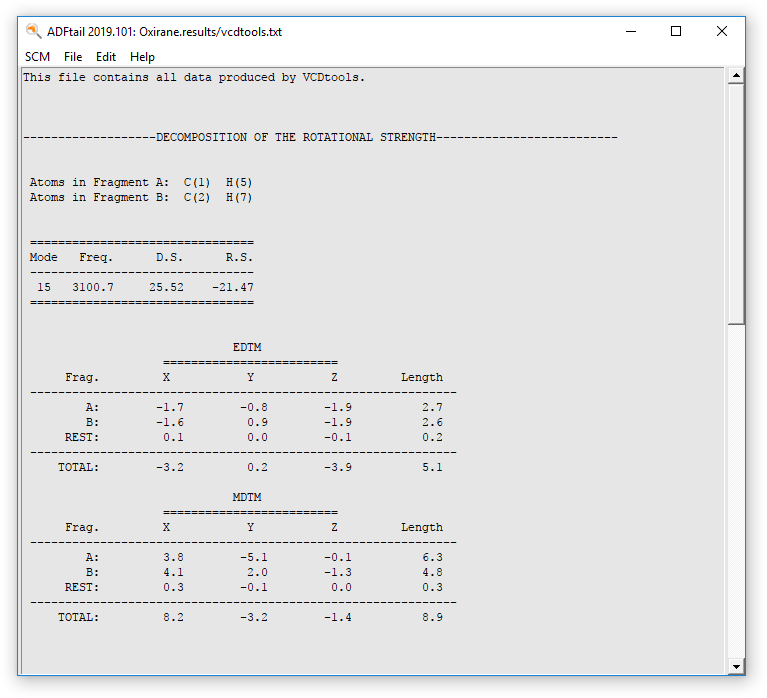
An ‘ADFtail’ window will now have opened showing the ‘vcdtools.txt’ file. In this file all output from VCDtools is stored. Each output entry begins by defining the settings such as the selected regions and normal modes. For normal mode 15 we see that indeed the major part of the VCD signal is caused by the GCO interaction between the two selected regions. The rest of the molecule barely contributes and also the VCD signal from the individual fragments is insignificant. We have thus successfully determined the source of the VCD intensity for normal mode 15.
If needed arrows can be shown inside the molecule to indicate the EDTM and the MDTM. This can be done per atom or per regions. For example:
- Select the VCDtools → EDTM Vectors (regional) command
Two arrows will have appeared at the geometric centers of the regions displaying the relative size and direction of the EDTMs.
Under the “VCDtools” menu there are many other commands. For example, VCDtools can guess the best fragments for GCO fragments and can compute the normal mode localization on the selected regions within the molecule. Feel free to test them out.