Ionic Liquids¶
6.1: Using the ADF COSMO-RS ionic liquid database¶
Ionic liquids (ILs), usually consisting of a large organic cation and a small inorganic polyatomic anion, have attracted considerable attention in recent years due to their unique thermophysical properties. The low vapor pressure and high conductivity of these molten salts combined with highly tunable properties, have resulted in highly diverse applications across many different fields in chemistry, materials science (battery electrolytes), chemical engineering (gas sorption and purification), and many more.
To calculate thermodynamic properties of ionic liquids with COSMO-RS, the IL may be described either as a single ion pair or as discrete cations and anions. The latter method will be mainly used here. The COSMO-RS ionic liquid database ADFCRS-IL-2014 contains 80 cations and 56 anions. This ADFCRS-IL-2014 database consists of ADF COSMO result (.coskf) files, from standard ADF quantum mechanical calculations, as described in tutorial 1: COSMO result files. The user can create new anions and cations using that same approach and add them to the List of Added Compounds.
The ADFCRS-IL-2014 database is part of the ADFCRS-2018 COSMO-RS database. Install the ADFCRS-2018 database if it is not yet installed, see tutorial 4: The COSMO-RS compound database.
SCM gratefully acknowledges Prof. Zhigang Lei’s research group (State Key Laboratory of Chemical Resource Engineering, Beijing University of Chemical Technology, China) for providing the ionic liquid database, the corresponding tutorial, and the reparameterization of COSMO-RS for ionic liquids (ADF Lei 2018).
Reparameterization of COSMO-RS for ionic liquids¶
In Ref. [617] Han, Lei and coworkers present a reparametrization of COSMO-RS parameters for ionic liquids within the ADF framework. The extensive training set consisted of 2283 activity coefficient data points at infinite dilution and 1433 CO2 solubility data points that were collected from literature references.
The authors use the refitted parameters to predict CO2 solubility in pure ionic liquids at low temperatures (<273.2 K) and the CO2 solubility in mixed ionic liquids over a wide temperature and pressure range.
Their refitted optimal values for the misfit energy constant a’, hydrogen bond coefficient c_hb and the effective contact surface area of a segment a_eff can be edited manually:
- Select Method → COSMO-RSSelect Method → ParametersSelect ‘ADF combi2005’ in the popup menu Use COSMO-RS parametersEnter 2063.0 for a’Enter 7532.0 for c_hbEnter 3.34 for a_eff
However, in this Tutorial we will use the original COSMO-RS parameters.
- Select Method → COSMO-RSSelect Method → ParametersSelect ‘ADF combi2005’ in the popup menu Use COSMO-RS parameters
References¶
Some of the work of Zhigang Lei group based on the COSMO-RS model using the ADF software is listed as follows:
- Z. Lei, C. Dai, J. Zhu, B. Chen, Extractive distillation with ionic liquids: A review, AIChE Journal 60, 3312 (2014)
- Z. Lei, C. Dai, B. Chen, Gas solubility in ionic liquids, Chemical Reviews 14, 1289 (2014)
- Z. Lei, J. Han, Q. Li, and B. Chen, Process Intensification on the Supercritical Carbon Dioxide Extraction of Low-Concentration Ethanol from Aqueous Solutions, Industrial & Engineering Chemistry research 51, 2730 (2012)
- Z. Lei, J. Han, B. Zhang, Q. Li, J. Zhu, and B. Chen, Solubility of CO2 in Binary Mixtures of Room-Temperature Ionic Liquids at High Pressures, Journal of Chemical Engineering data 57, 2153 (2012)
- Z. Lei, C. Dai, X. Liu, L. Xiao, and B. Chen, Extension of the UNIFAC Model for Ionic Liquids, Industrial & Engineering Chemistry research 51, 12135 (2012)
- Z. Lei, C. Dai, Q. Yang, J. Zhu, and B. Chen, UNIFAC model for ionic liquid-CO (H2 ) systems: An experimental and modeling study on gas solubility, AIChE Journal 60, 4222 (2014)
- J. Han, C. Dai, G. Yu, Z. Lei, Parameterization of COSMO-RS model for ionic liquids, Green Energy & Environment 3, 247 (2018)
6.2: Ionic liquid volumes and densities¶
Ionic liquid densities may be estimated from the molecular volume and molar mass (MW) of the constituent cations and anions. The COSMO volume is stored in the coskf file and is displayed, together with the MW, when a compound is selected in the COSMO-RS GUI.
- Click on the search button in the compounds fieldSelect IL_cation_1-butyl-3-methyl-imidazoliumClick OK

Volumes and molar mass of other cations and anions can be similarly found. Data for a few compounds are listed below.
| COSMO Volume (Å 3) | MW (g/mol) | |
|---|---|---|
| cations | ||
| C4MIM 1-butyl-3-methyl-imidazolium | 197.181 | 139.124 |
| C6MIM 1-hexyl-3-methyl-imidazolium | 241.003 | 167.155 |
| C8MIM 1-octyl-3-methyl-imidazolium | 282.855 | 195.186 |
| anions | ||
| BF4 tetrafluoroborate | 72.489 | 87.003 |
| PF6 hexafluorophosphate | 103.495 | 144.964 |
| NTF2 bis(trifluoromethylsulfonyl)amide | 213.173 | 279.917 |
The molecular liquid density could be approximately calculated as (V in Å3 and MW in g/mol) using Avogadro’s number:
- density = (MWcation + MWanion )/[0.6022*(Vcation + Vanion )]
| ionic liquid | expt [621] | calculated |
|---|---|---|
| C4MIMBF4 | 1.208 | 1.392 |
| C6MIMBF4 | 1.148 | 1.346 |
| C8MIMBF4 | 1.109 | 1.319 |
| C4MIMPF6 | 1.37 | 1.569 |
| C6MIMPF6 | 1.293 | 1.505 |
| C8MIMPF6 | 1.237 | 1.462 |
| C4MIMNTf2 | 1.429 | 1.696 |
| C6MIMNTf2 | 1.37 | 1.635 |
| C8MIMNTf2 | 1.32 | 1.591 |
As can be seen from this table, the calculated densities are systematically overestimated by approximately 15%. Thus, the COSMO volumes underestimate the volume of a single compound, if they are used for estimating the liquid densities.
References¶
- C. Ye and J.M. Shreeve, Rapid and Accurate Estimation of Densities of Room-Temperature Ionic Liquids and Salts, Journal of Physical Chemistry A 111, 1456 (2007)
6.3: Activity coefficient calculation¶
The activity coefficient of a compound i solvated in an ionic liquid is an important thermodynamic property. The cation and anion, which have been treated separately, will be used in equal amounts to ensure an electroneutral mixture in the COSMO-RS calculation.
In other applications cation-anion pair have been treated as one molecule, however, in the COSMO-RS calculations below we will treat the cation and anion as two separate molecules. This has consequences for the value of the activity coefficients.
For example, for a 1:1 IL (i.e., [A]+ [B]- ), the activity coefficient at a finite concentration of solute i in the binary mixture (IL + solute) can be calculated by
- γi bin = (γi tern xi tern )/xi bin = γi tern /(1+xIL bin )
where the superscript “tern” represents the hypothetical ternary system comprising cation, anion and solute i, with
- xcation tern = xanion tern
- xcation tern + xanion tern + xi tern = 1
and the superscript “bin” represents the binary mixture comprising solute and IL, with
- xIL bin + xi bin = 1
Accordingly, the activity coefficient of a solute i in the binary mixture (IL + solute) at infinite dilution is simplified as
- γi bin = 0.5 γi tern (at infinite dilution)
Thus in this case we should scale the activity coefficient at infinite dilution γi tern , which is directly obtained from the COSMO-RS calculation, with a factor of 0.5.
Similarly, for a ternary system comprising component i, component j and an ionic liquid, the activity coefficient at finite concentration of component i can be calculated by
- γi tern = γi quart /(1+xIL tern )
where the superscript “quart” represents the hypothetical quaternary system comprised of cation, anion, solute i and solute j, with:
- xcation quart = xanion quart
- xcation quart + xanion quart + xi quart + xj quart = 1
and the superscript “tern” represents the ternary mixture comprising solute i, j, and IL, with
- xIL tern + xi tern + xj tern = 1
- Select Properties → Activity coefficientsSelect ‘2 components’ in the popup menu next to SolventSelect ‘IL_cation_1-ethyl-3-methyl-imidazolium’ for the first component in SolventEnter 0.5 for the Mole fraction of the first componentSelect ‘IL_anion_tetracyanoborate’ for the second component in SolventEnter 0.5 for the Mole fraction of the second componentEnter ‘308.15’ for ‘Temperature Kelvin’Check the ‘+’ button to add ‘Hexane’, ‘Heptane’, ‘Octane’, and ‘Decane’Press ‘Run’

If one does not supply a density of the solvent in the input, the program calculates the density of the solvent by dividing the mass of a molecule with its COSMO volume. Note that the calculated activity coefficients do not depend on this density. The result of the calculation is given in the form of a table.

Note that for a comparison to experimental numbers, the calculated activity coefficients have to be scaled with 0.5, as was discussed before. In the next figure the results of the calculated activity coefficients at different temperatures are compared to experiment.

In this figure activity coefficients at infinite dilution of n-alkenes in [EMIM]+ [TCB]- are shown for different temperatures ranging from 298 K to 358 K. The scattered points are experimental data from Ref.[633]. The points that are connected with a line are calculated numbers with ADF COSMO-RS. For example, for Hexane, the calculated values T = 308.15 K are: 1000/308.15 = 3.245, ln(0.5*60.439) = 3.41. Note that the calculated numbers in this figure are calculated with an older version of COSMO-RS. These will not change much if you use a newer COSMO-RS version.
References¶
- Z. Lei, C. Dai, J. Zhu, B. Chen, Extractive distillation with ionic liquids: A review, AIChE Journal 60, 3312 (2014)
- Z. Lei, C. Dai, B. Chen, Gas solubility in ionic liquids, Chemical Reviews 14, 1289 (2014)
- U. Domańska, M. Królikowska, W.E. Acree Jr., G.A. Baker, Activity coefficients at infinite dilution measurements for organic solutes and water in the ionic liquid 1-ethyl-3-methylimidazolium tetracyanoborate, The Journal of Chemical Thermodynamics 43, 1050 (2011)
6.4: Henry’s law constants¶
In this tutorial, we will calculate Henry’s law constants for CO2 in different ionic liquids. Henry’s law constant reflects the solubility of a gas in a solvent, and one way to define it is
where Hi is the ratio between the partial vapor pressure of a compound i in the gas phase and its molar fraction in the liquid phase, \(\gamma_i^\infty\) is the the activity coefficient of the compound at infinite dilution, and Pi S is the saturated pure compound vapor pressure of the gas.
The familiar Antoine and Wagner equations can be used to calculate the vapor pressure below the critical temperature Tc , if one knows the coefficients. Above Tc , they can be extrapolated as a hypothetical vapor pressure. If the experimental saturated vapor pressures of a gas is not available, then it can be estimated by COSMO-RS.
The saturated vapor pressure of CO2 at 298.15 K can be calculated by the following Antoine equation:
- ln PCO2 S (MPa) = 12.3312 - 4759.46/(T(K)+156.462)
The saturated vapor pressure of CO2 at 298.15 K is 6.436 MPa (= 64.36 bar) according to this equation. The Antoine equation can also be written as:
- \({}^{10}\)log PCO2 S (bar) = 6.35537 - 2067.0/(T(K)+156.462)
The activity coefficients of infinitely diluted carbon dioxide in [HMIM]+ [Tf2N]- will now be calculated.
- Select Compounds → List of Added CompoundsSearch on the left side ‘Carbon dioxide’ and click on itEnter 6.35537 for the Antoine coefficient A on the right sideEnter 2067.0 for the Antoine coefficient BEnter 156.462 for the Antoine coefficient CSelect Properties → Activity coefficientsSelect ‘2 components’ in the popup menu next to SolventSelect ‘IL_cation_1-hexyl-3-methyl-imidazolium’ for the first component in SolventEnter 0.5 for the Mole fraction of the first componentSelect ‘IL_anion_bis(trifluoromethylsulfonyl)amide’ for the second component in SolventEnter 0.5 for the Mole fraction of the second componentEnter ‘298.15’ for ‘Temperature Kelvin’Check the ‘+’ button to add ‘Carbon dioxide’ (Remove the alkanes if they are still present)Press ‘Run’

The results of the activity coefficients.

As discussed before, we should scale the COSMO-RS calculated activity coefficient at infinite dilution \(\gamma^\infty\) with a factor of 0.5. Henry’s law coefficient is \(\gamma^\infty\) times the saturated vapor pressure of CO2 at 298.15 K (64.36 bar). For CO2 in [HMIM]+ [Tf2N]- the calculated H = 0.5*1.01305*64.36 = 32.6 bar. Applying the same calculations for more ionic liquids gives these results:
| ionic liquid | expt [644] | calculated |
|---|---|---|
| BMIM PF6 | 53.4±0.3 | 53.1 |
| BMIM Tf2 N | 33.0±0.3 | 35.4 |
| HMIM Tf2 N | 31.6±0.2 | 32.6 |
| HMPY Tf2 N | 28.4±0.2 | 314 |
| C6F9MIM Tf2 N | 27.3±0.1 | 33.8 |
| C8F13MIM Tf2 N | 25.2±0.2 | 31.0 |
| HMIM eFAP | 25.2±0.1 | 27.1 |
| HMIM pFAP | 21.6±0.1 | 25.8 |
| C5MIM bFAP | 20.2±0.1 | 25.2 |
| Et3 NBH2 MIM Tf2 N | 33.1±1.2 | 30.5 |

There are many different definitions of Henry’s law constant. Henry’s constant as calculated directly by COSMO-RS, kH (mol/(L atm)), is defined as the ratio between the liquid phase concentration of a compound and its partial vapor pressure in the gas phase. The relationship between kH and H is:
- H = kH,inv px = 1/(kH Vsolvent )
where Vsolvent is the molar volume of the ionic liquid. If no densities for the cation, anion, or solvent are given, COSMO-RS will use the COSMO volume for calculating the molar volume of the ionic liquid, which is 0.2735 L/mol (=(241.00+213.17)*0.6022/1000) for [HMIM]+ [Tf2N]- , if the usual convention is followed, that a pair of a cation and an anion is treated as one molecule. Thus in this case H = 1.01325/(0.1136 * 0.2735) = 32.6 bar, where a conversion factor from atm to bar is included.
Note that kH does not depend on whether one treats a cation and an anion as separate molecules, or if a pair of a cation and an anion is treated as one molecule. H = kH,inv px does depend on this definition.
References¶
- P.G.T. Fogg and W. Gerrard, Solubility of gases in liquids: A critical evaluation of gas/liquid systems in theory and practice, New York: John Wiley & Sons, Inc., 1991.
- J.L. Anthony, J.L. Anderson, E.J. Maginn, J.F. Brennecke, Anion Effects on Gas Solubility in Ionic Liquids, Journal of Physical Chemistry B 109, 6366 (2005)
- J.L. Anderson, E. J. Maginn and J. F. Brennecke, Measurement of SO2 Solubility in Ionic Liquids, Journal of Physical Chemistry B 110, 15059 (2006)
- M.J. Muldoon, S.N.V.K. Aki, J.L. Anderson, J.K. Dixon, J.F. Brennecke, Improving Carbon Dioxide Solubility in Ionic Liquids, Journal of Physical Chemistry B 111, 9001 (2007)
- B.H. Culbertson, S. Dai, H. Luo, D.W. DePaoli, Low-Pressure Solubility of Carbon Dioxide in Room-Temperature Ionic Liquids Measured with a Quartz Crystal Microbalance, Journal of Physical Chemistry B 108, 721 (2004)
- Y. Hou and R.E. Baltus, Experimental Measurement of the Solubility and Diffusivity of CO2 in Room-Temperature Ionic Liquids Using a Transient Thin-Liquid-Film Method, Industrial & Engineering Chemistry research 46, 8166 (2007)
- A. Finotello, J.E. Bara, D. Camper and R.D. Noble, Room-Temperature Ionic Liquids: Temperature Dependence of Gas Solubility Selectivity, Industrial & Engineering Chemistry research 47, 3453 (2008)
6.5: Gas solubility and selectivity in ionic liquids¶
In this example the solubility of carbon dioxide in ionic liquids is calculated and compared to experimental data.
In the ADF COSMO-RS calculation, an ionic liquid molecule is described as a discrete cation and anion. Thus, the system of gas and ionic liquid will be treated as a hypothetical ternary mixture (“tern”) consisting of gas, cation, and anion. For a 1:1 ionic liquid, the solubility of gas xgas tern in the hypothetical ternary system can be calculated by
- xgas tern = ngas /(ngas + ncation +nanion ) = ngas /(ngas + 2nIL )
where xgas tern is the molar fraction of the gas in the hypothetical ternary system, and ngas , ncation , nanion , and nIL are the molar amounts of gas, cation, anion, and IL in the liquid phase, respectively. For the real gas and IL binary system, the gas solubility x (molar fraction of the gas in the IL) is defined as:
- x = ngas /(ngas + nIL )
Combining the previous equations yields:
- x = 2 xgas tern /(xgas tern + 1)
First we use the experimental Antoine coefficients for CO2 .
- (Skip this part if you have just done COSMO-RS tutorial 6.4)Select Compounds → List of Added CompoundsSearch on the left side ‘Carbon dioxide’ and click on itEnter 6.35537 for the Antoine coefficient A on the right sideEnter 2067.0 for the Antoine coefficient BEnter 156.462 for the Antoine coefficient C
Next we calculate CO2 solubilities.
- Select Properties → Solubility in MixtureSelect ‘2 components’ in the popup menu next to SolventSelect ‘IL_cation_1-hexyl-3-methyl-imidazolium’ for the first component in SolventEnter 0.5 for the Mole fraction of the first componentSelect ‘IL_anion_bis(trifluoromethylsulfonyl)amide’ for the second component in SolventEnter 0.5 for the Mole fraction of the second componentEnter ‘8’ for ‘Temperature: number of steps’Enter ‘282.0’ for ‘Temperature from’Enter ‘322.8’ for ‘Temperature to’Change the popup menu next to Solutes to ‘Gas’Enter ‘3’ for ‘Pressure: for solubility gas: number of steps’Use ‘MPa’ units for the pressureEnter ‘0.5’ for the pressure ‘from’Enter ‘2.0’ for the pressure ‘to’Check the ‘+’ button to add ‘Carbon dioxide’Press ‘Run’
From the results we will use the calculated mole fractions at 282.0 K, 297.3 K, and 322.8 K.

Do the same calculation for a number of vapor pressures of Carbon dioxide, namely 0.5 MPa, 1.0 MPa, and 1.5 MPa. Remember that we need to convert the calculated solubilities xgas tern to the solubility x in the binary system, consisting of gas and IL, with x = 2 xgas tern /(xgas tern + 1):
| Temperature | P (MPa) | x tern | x |
|---|---|---|---|
| 282.0 | 0.5 | 0.103 | 0.186 |
| 282.0 | 1.0 | 0.206 | 0.341 |
| 282.0 | 1.5 | 0.310 | 0.473 |
| 282.0 | 2.0 | 0.415 | 0.587 |
| 297.3 | 0.5 | 0.072 | 0.134 |
| 297.3 | 1.0 | 0.144 | 0.252 |
| 297.3 | 1.5 | 0.216 | 0.356 |
| 297.3 | 2.0 | 0.289 | 0.448 |
| 322.8 | 0.5 | 0.042 | 0.081 |
| 322.8 | 1.0 | 0.084 | 0.155 |
| 322.8 | 1.5 | 0.126 | 0.223 |
| 322.8 | 2.0 | 0.168 | 0.287 |
In this example we also calculated the solubility of carbon dioxide at relatively high pressures. In this case, for more accurate results, we also need to take the nonideal behavior of the gas into account, the gas fugacity.
- fgas = Pgas \(\Phi\) (T,P)
where fgas is the gas fugacity at the system temperature and pressure, and \(\Phi\) (T,P) is the fugacity coefficiency of the gas. We will approximate the fugacity coefficients with:
Note that these values are only approximate, and certainly not applicable for higher pressures. We can use the same solubilities as calculated before but plot them against fugacity instead of pressure.
| Temperature | f (MPa) | P (MPa) |
|---|---|---|
| 282.0 | 0.50 | 0.52 |
| 282.0 | 1.00 | 1.07 |
| 282.0 | 1.50 | 1.67 |
| 282.0 | 2.00 | 2.32 |
| 297.3 | 0.50 | 0.51 |
| 297.3 | 1.00 | 1.06 |
| 297.3 | 1.50 | 1.63 |
| 297.3 | 2.00 | 2.25 |
| 322.8 | 0.50 | 0.51 |
| 322.8 | 1.00 | 1.04 |
| 322.8 | 1.50 | 1.60 |
| 322.8 | 2.00 | 2.19 |
The results can be compared with experimental values from Ref.[651]. Note that the calculated numbers in this figure are calculated with an older version of COSMO-RS. These will not change much if you use a newer COSMO-RS version.

For low pressures one can estimate gas solubility using Henry’s law constants:
For low pressures \(\Phi\) (T,P) will be close to 1. Calculating Henry’s law constants has been described in COSMO-RS Tutorial 6.4, and following this procedure for CO2 in [HMIM][Tf2 N], results in H = 2.24 MPa at T = 282 K, H = 3.20 MPa at T = 297.3 K, and H = 5.51 MPa at T = 322.8 K.
Gas selectivity in ionic liquids can be defined as
- Si/j = Hi /Hj
where Si/j is the selectivity between gas i and j in ionic liquids; Hi and Hj are Henry’s law constants of gas i and j, which can be calculated using the methods as described in the COSMO-RS Tutorial 6.4.
References¶
- M.B. Shiflett and A. Yokozeki, Solubility of CO2 in Room Temperature Ionic Liquid [hmim][Tf2 N], Journal of Physical Chemistry B 111, 2070 (2007)
6.6: VLE for systems containing ionic liquids¶
In this example a vapor-liquid diagram of Acetone in [EMIM][Tf2 N] at 353.15 K is calculated and compared to experiment. The experimental saturated pure compound vapor pressure is used for Acetone.
- Select Compounds → List of Added CompoundsSearch on the left side ‘Acetone’ and click on itEnter ‘2.1516’ in the ‘Pure compound vapor pressure’ fieldEnter ‘353.15’ in the ‘at temperature’ fieldSelect Properties → Solvents s1 - s2 Composition LineSelect ‘3 components’ in the popup menu next to SolventsSelect ‘Acetone’ for the first component in SolventsSelect ‘IL_cation_1-ethyl-3-methyl-imidazolium’ for the second component in SolventSelect ‘IL_anion_bis(trifluoromethylsulfonyl)amide’ for the third component in SolventEnter ‘1.0’ for the mole fraction of compound 1 of solvent s1Enter ‘0.0’ for the mole fraction of compound 1 of solvent s2Enter ‘0.0’ for the mole fraction of compound 2 of solvent s1Enter ‘0.5’ for the mole fraction of compound 2 of solvent s2Enter ‘0.0’ for the mole fraction of compound 3 of solvent s1Enter ‘0.5’ for the mole fraction of compound 3 of solvent s2Enter ‘20’ for ‘Number of mixtures’Select ‘Isotherm’ from the Isotherm, isobar, flash point popup menuUse ‘Kelvin’ as units for the temperatureEnter ‘353.15’ for ‘Temperature’Press ‘Run’

Remember that, before we compare to experiment, we need to convert the calculated molar fractions xi tern from the hypothetical ternary system to the molar fractions xi bin in the binary acetone-IL system with:
- xi bin = 2 xi tern /(xi tern + 1)xi tern = xi bin /(2 - xi bin )
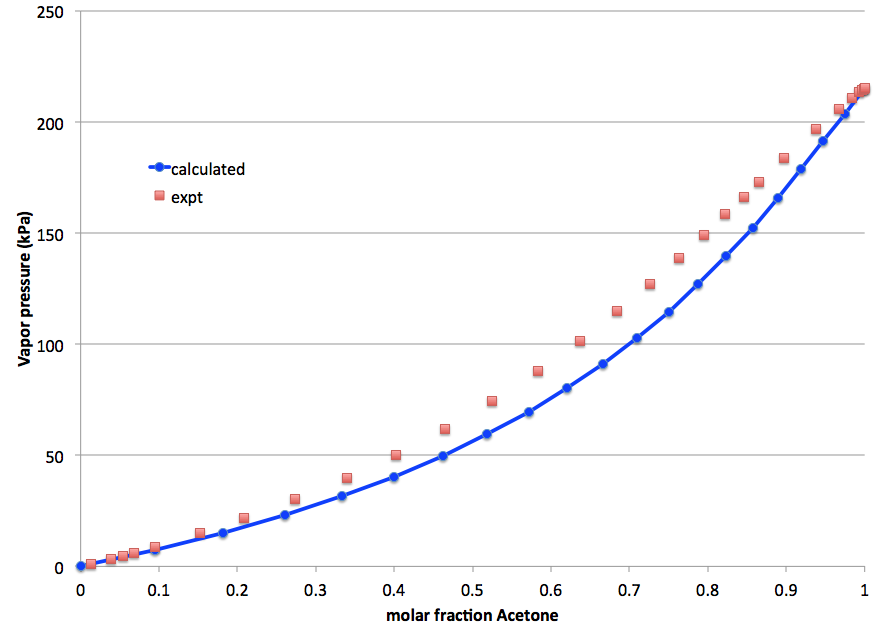
| xtern | xbin | P (kPa) | xbin | P (kPa) |
| calc | calc | calc | expt [661] | expt [661] |
| 0.00 | 0.0000 | 0.000 | 0.0133 | 1.139 |
| 0.05 | 0.0952 | 7.376 | 0.0383 | 3.485 |
| 0.10 | 0.1818 | 15.098 | 0.0539 | 4.825 |
| 0.15 | 0.2609 | 23.183 | 0.0683 | 6.073 |
| 0.20 | 0.3333 | 31.648 | 0.0949 | 8.509 |
| 0.25 | 0.4000 | 40.511 | 0.1521 | 14.884 |
| 0.30 | 0.4615 | 49.788 | 0.2081 | 21.660 |
| 0.35 | 0.5185 | 59.493 | 0.2735 | 30.115 |
| 0.40 | 0.5714 | 69.638 | 0.3393 | 39.811 |
| 0.45 | 0.6207 | 80.232 | 0.4022 | 50.263 |
| 0.50 | 0.6667 | 91.275 | 0.4647 | 61.862 |
| 0.55 | 0.7097 | 102.76 | 0.5249 | 74.281 |
| 0.60 | 0.7500 | 114.68 | 0.5839 | 87.870 |
| 0.65 | 0.7879 | 126.99 | 0.6369 | 101.46 |
| 0.70 | 0.8235 | 139.65 | 0.6846 | 114.73 |
| 0.75 | 0.8571 | 152.57 | 0.7264 | 127.22 |
| 0.80 | 0.8889 | 165.63 | 0.7631 | 138.75 |
| 0.85 | 0.9189 | 178.69 | 0.7948 | 149.16 |
| 0.90 | 0.9474 | 191.51 | 0.8222 | 158.37 |
| 0.95 | 0.9744 | 203.79 | 0.8455 | 166.29 |
| 1.00 | 1.0000 | 215.16 | 0.8653 | 173.07 |
| 0.8967 | 183.75 | |||
| 0.9376 | 196.92 | |||
| 0.9671 | 205.80 | |||
| 0.9844 | 210.74 | |||
| 0.9933 | 213.25 | |||
| 0.9972 | 214.40 | |||
| 0.9990 | 214.94 | |||
| 1.0000 | 215.16 |
Comparing the calculated and experimental vapor pressure of acetone in [EMIM][Tf2N] in a graph:
References
- M. Döker, J. Gmehling Measurement and prediction of vapor–liquid equilibria of ternary systems containing ionic liquids, Fluid Phase Equilibria 227 (2005), 255